Phương pháp: Để tìm tập hợp điểm $M$ ta có thể quy về tìm tập hợp điểm $N$ và tìm một phép vị tự ${{V}_{\left( I;k \right)}}$ nào đó sao cho ${{V}_{\left( I;k \right)}}\left( N \right)=M$ suy ra quỹ tích điểm $M$ là ảnh của quỹ tích $N$ qua ${{V}_{\left( I;k \right)}}$.
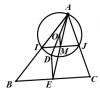
Ví dụ 6. Cho đường tròn $\left( O;R \right)$ và một điểm $I$ nằm ngoài đường tròn sao cho $OI=3R$, $A$ là một điểm thay đổi trên đường tròn $\left( O;R \right)$. Phân giác trong góc $\widehat{IOA}$ cắt $IA$ tại điểm $M$. Tìm tập hợp điểm $M$ khi $A$ di động trên $\left( O;R \right)$.

Theo tính chất đường phân giác ta có $\frac{{MI}}{{MA}} = \frac{{OI}}{{OA}} = \frac{{3R}}{R} = 3$ $ \Rightarrow IM = \frac{3}{4}IA$ $ \Rightarrow \overrightarrow {IM} = \frac{3}{4}\overrightarrow {IA} .$
Suy ra ${{V}_{\left( I;\frac{3}{4} \right)}}\left( A \right)=M$, mà $A$ thuộc đường tròn $\left( O;R \right)$ nên $M$ thuộc $\left( O’;\frac{3}{4}R \right)$ ảnh của $\left( O;R \right)$ qua ${{V}_{\left( I;\frac{3}{4} \right)}}$.
Vậy tập hợp điểm $M$ là $\left( O’;\frac{3}{4}R \right)$ ảnh của $\left( O;R \right)$ qua ${{V}_{\left( I;\frac{3}{4} \right)}}$.
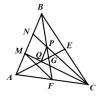
Ví dụ 7. Cho tam giác $ABC$. Qua điểm $M$ trên cạnh $AB$ vẽ các đường song song với các đường trung tuyến $AE$ và $BF$, tương ứng cắt $BC$ và $CA$ tai $P,Q$ . Tìm tập hợp điểm $R$ sao cho $MPRQ$ là hình bình hành.

Gọi $I = MQ \cap AE$, $K = MP \cap BF$ và $G$ là trọng tâm của tam giác $ABC.$
Ta có: $\frac{{MI}}{{BG}} = \frac{{AM}}{{AB}} = \frac{{AQ}}{{AF}} = \frac{{IQ}}{{GF}}$ $ \Rightarrow \frac{{MI}}{{IQ}} = \frac{{BG}}{{GF}} = 2$ $ \Rightarrow \overrightarrow {MI} = \frac{2}{3}\overrightarrow {MQ} .$
Tương tự ta có $\overrightarrow {MK} = \frac{2}{3}\overrightarrow {MP} .$
Từ đó ta có $\overrightarrow {MG} = \overrightarrow {MI} + \overrightarrow {MK} $ $ = \frac{2}{3}\overrightarrow {MQ} + \frac{2}{3}\overrightarrow {MP} $ $ = \frac{2}{3}\overrightarrow {MR} .$
Do đó $\overrightarrow {GR} = – \frac{1}{2}\overrightarrow {GM} $ $ \Rightarrow {V_{\left( {G; – \frac{1}{2}} \right)}}\left( M \right) = R.$
Mà $M$ thuộc cạnh $AB$ nên $R$ thuộc ảnh của cạnh $AB$ qua ${{V}_{\left( G;-\frac{1}{2} \right)}}$ đoạn chính là đoạn $EF$.
Vậy tập hợp điểm $R$ là đoạn $EF$.
Ví dụ 6. Cho đường tròn $\left( O;R \right)$ và một điểm $I$ nằm ngoài đường tròn sao cho $OI=3R$, $A$ là một điểm thay đổi trên đường tròn $\left( O;R \right)$. Phân giác trong góc $\widehat{IOA}$ cắt $IA$ tại điểm $M$. Tìm tập hợp điểm $M$ khi $A$ di động trên $\left( O;R \right)$.
Theo tính chất đường phân giác ta có $\frac{{MI}}{{MA}} = \frac{{OI}}{{OA}} = \frac{{3R}}{R} = 3$ $ \Rightarrow IM = \frac{3}{4}IA$ $ \Rightarrow \overrightarrow {IM} = \frac{3}{4}\overrightarrow {IA} .$
Suy ra ${{V}_{\left( I;\frac{3}{4} \right)}}\left( A \right)=M$, mà $A$ thuộc đường tròn $\left( O;R \right)$ nên $M$ thuộc $\left( O’;\frac{3}{4}R \right)$ ảnh của $\left( O;R \right)$ qua ${{V}_{\left( I;\frac{3}{4} \right)}}$.
Vậy tập hợp điểm $M$ là $\left( O’;\frac{3}{4}R \right)$ ảnh của $\left( O;R \right)$ qua ${{V}_{\left( I;\frac{3}{4} \right)}}$.
Ví dụ 7. Cho tam giác $ABC$. Qua điểm $M$ trên cạnh $AB$ vẽ các đường song song với các đường trung tuyến $AE$ và $BF$, tương ứng cắt $BC$ và $CA$ tai $P,Q$ . Tìm tập hợp điểm $R$ sao cho $MPRQ$ là hình bình hành.
Gọi $I = MQ \cap AE$, $K = MP \cap BF$ và $G$ là trọng tâm của tam giác $ABC.$
Ta có: $\frac{{MI}}{{BG}} = \frac{{AM}}{{AB}} = \frac{{AQ}}{{AF}} = \frac{{IQ}}{{GF}}$ $ \Rightarrow \frac{{MI}}{{IQ}} = \frac{{BG}}{{GF}} = 2$ $ \Rightarrow \overrightarrow {MI} = \frac{2}{3}\overrightarrow {MQ} .$
Tương tự ta có $\overrightarrow {MK} = \frac{2}{3}\overrightarrow {MP} .$
Từ đó ta có $\overrightarrow {MG} = \overrightarrow {MI} + \overrightarrow {MK} $ $ = \frac{2}{3}\overrightarrow {MQ} + \frac{2}{3}\overrightarrow {MP} $ $ = \frac{2}{3}\overrightarrow {MR} .$
Do đó $\overrightarrow {GR} = – \frac{1}{2}\overrightarrow {GM} $ $ \Rightarrow {V_{\left( {G; – \frac{1}{2}} \right)}}\left( M \right) = R.$
Mà $M$ thuộc cạnh $AB$ nên $R$ thuộc ảnh của cạnh $AB$ qua ${{V}_{\left( G;-\frac{1}{2} \right)}}$ đoạn chính là đoạn $EF$.
Vậy tập hợp điểm $R$ là đoạn $EF$.