giáo án Tổng hợp hai dao động điều hòa cùng phương cùng tần số. Phương pháp giản đồ FRE-NEN

[Doremon]

I. Véc tơ quay
Dao động điều hòa: x = Acos(ωt + φ)
Được biểu diễn bằng véc tơ quay $\mathop {OM}\limits^{ - - \to }$ có

• Gốc tại gốc tọa độ của trục Ox.
• Độ dài bằng biên độ dao động: OM = A.
• Hợp với trục Ox một góc bằng φ.
• Quay đều quanh O theo chiều dương (ngược chiều kim đồng hồ) với vận tốc góc ω.

II. Phương pháp giãn đồ Fre-nen

1. Đặt vấn đề

• Xét hai dao động điều hòa cùng phương cùng tần số: x$_1$ = A$_1$cos(ωt + φ$_1$) và x$_2$ = A$_2$cos(ωt + φ$_2$)
• Để tìm li độ dao động tổng hợp x = x$_1$ + x$_2$ trong trường hợp A$_1$ ≠ A$_2$ ta dùng phương pháp giãn đồ Fre-nen.

2. Phương pháp giãn đồ Fre-nen
a) Biểu diễn các dao động thành phần và dao động tổng hợp bằng véc tơ quay

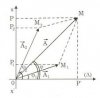
• Các dao động thánh phần x$_1$ và x$_2$ được biểu diễn bởi hai véc tơ quay $\mathop {O{M_1}}\limits^{ - - \to } $ và $\mathop {O{M_2}}\limits^{ - - \to } $ khi đó dao động tổng hợp x = x$_1$ + x$_2$ được biểu diễn bởi véc tơ quay $\mathop {OM}\limits^{ - - \to } $ với $\overrightarrow {OM} = \overrightarrow {O{M_1}} + \overrightarrow {O{M_2}} $
• Vậy, dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số là một dao động điều hòa cùng phương, cùng tần số với hai dao động thành phần.

b) Biên độ và pha ban đầu của dao động tổng hợp.
Dựa vào giãn đồ véc tơ ta thấy:
$\begin{array}{l}{A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \left( {{\varphi _2} - {\varphi _1}} \right)\\
\tan \varphi = \frac{{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}}}{{{A_1}\cos {\varphi _1} + {A_2}\cos {\varphi _2}}}\end{array}$

3. Ảnh hưởng của độ lệch pha

• Biên độ và pha ban đầu của dao động tổng hợp phụ thuộc vào biên độ và pha ban đầu của các dao động thành phần.
• Khi hai dao động thành phần cùng pha (φ$_2$ - φ$_1$ = 2kπ) thì dao động tổng hợp có biên độ cực đại: A = A$_1$ + A$_2$
• Khi hai dao động thành phần ngược pha (φ$_2$ - φ$_1$ = (2k + 1)π) thì dao động tổng hợp có biên độ cực tiểu: A = |A$_1$ - A$_2$| .
• Trường hợp tổng quát: A$_1$ + A$_2$ ≤ A ≤|A$_1$ - A$_2$| .

4. Ví dụ
Tìm phương trình dao động tổng hợp của hai dao động thành phần sau:

x$_1$ = 4cos(10πt + π/3) (cm)
x$_2$ = 2cos(10πt + π) (cm)​

• Ta có: A$_2$ = A$_1$ + A$_2$ + 2 A$_1$A$_2$ cos (φ$_2$ - φ$_1$) = 16 + 4 + 16.(-0,5) = 12 → A = 2√3 (cm).

$\tan \varphi = \frac{{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}}}{{{A_1}\cos {\varphi _1} + {A_2}\cos {\varphi _2}}} = \frac{{4.\frac{{\sqrt 3 }}{2} + 2.0}}{{4.0,5 + 2.( - 1)}} = \infty = \tan \left( {\frac{\pi }{2}} \right)$

• Vậy phương trình dao động tổng hợp là: $x = 2\sqrt 3 cos(10\pi t + \frac{\pi }{2})\;(cm)$

Tải về

 

[Mybabyminhchau]

giúp e câu này với th ơi
Cho 2 chất điểm dao động x$_1$, x$_2$ có chung vị trí cân bằng, chung gốc thời gian t = 0. Biết x$_1$ = 4 cos(4πt - π/4) và x$_2$ = 4cos(2πt+π/6) . hỏi khi x$_1$ gặp x$_2$ lần thứ 2013 thì t=??
A .18019/36
B.12073/36
C. 4025/4
D. 8653/4

 

[Hoàng Minh Nguyệt]

giúp e câu này với th ơi . cho 2 chất điểm dao động x1,x2 có chung vị trí cân bằng , chung gốc thời gian t=0 . Biết x1=4 cos(4pit-pi/4) và x2=4cos(2pit+pi/6) . hỏi khi x1 gặp x2 lần thứ 2013 thì t=?? A .18019/36 ; B.12073/36 ; C4025/4 .D 8653/4

bài này cậu chỉ cần viết phương trình x = x$_1$ - x$_2$ sau đó sử dụng phương pháp đường tròn tìm cho thời gian vật đi qua vị trí x = 0 là ok mà

 

[Hoàng Dũng]

@Hoàng Minh Nguyệt giải chi tiết giúp với

 

[Hoàng Minh Nguyệt]

@Hoàng Minh Nguyệt giải chi tiết giúp với

câu viết được phương trình tổng hợp rồi sau đó áp dụng theo ví dụ 5 như link này: https://tanggiap.net/threads/ung-dung-duong-tron-luong-giac-de-giai-cac-bai-lien-quan-toi-li-do.255/

 

[Doremon]

@Hoàng Minh Nguyệt lưu ý là bài của bạn ý với x$_1$ và x$_2$ có tần số góc ${\omega _1} = 4\pi \left( {\frac{{rad}}{s}} \right);\,{\omega _2} = 2\pi \left( {\frac{{rad}}{s}} \right)$ nhé

 

[Doremon]

${x_1} = {x_2} \to \left[ \begin{array}{l}{t_1} = \frac{1}{4} + k\left( 1 \right)\\{t_2} = \frac{1}{{36}} + \frac{\ell }{3}\left( 2 \right)\end{array} \right.$
gặp nhau lần 2013 ứng với họ nghiệm (2) nghĩa là : ℓ = 1006 → Đáp án B

 

[Mybabyminhchau]

Admin có thể giúp tui gi ải thích tại sao gặp nhau lần 2013 ứng với họ nghiệm (2) ko ah

 

[Huy Hoàng]

Admin có thể giúp tui gi ải thích tại sao gặp nhau lần 2013 ứng với họ nghiệm (2) ko ah

Mình thay admin giải chi tiết hèm còn chọn nghiệm cũng dễ bạn ơi:
So sánh hai họ nghiệm thì ta thấy 1/36 s là thời gian nhỏ nhất hai vật gặp nhau--> ưng với lần 1 ( số lẻ)
Với 1/4 s là lần thứ hai mà hai vật gặp nhau ( số chắn)
Ta thấy 2013 là số lẻ nên úng với họ (2) và l = 1006

 

[Huy Hoàng]

@Mybabyminhchau thấy hay ủng hô tinh thần bằng nút like cái nhé ))))

 

[Mybabyminhchau]

Nhưng Huy Hoàng ơi :tại sao lại biết 1/4 là lần gặp nhau thư 2 nhỉ

 

[Huy Hoàng]

Nhưng Huy Hoàng ơi :tại sao lại biết 1/4 là lần gặp nhau thư 2 nhỉ

Vì thời gian t không âm nên Bạn thử tìm giá trị nhỏ nhất của l và k thay vào thì thấy 1/36 là nhỏ nhất sau đó đến 1/4 thôi
Vi

 

[Tăng Giáp]

Một vật tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số, nhưng vuông pha nhau, có biên độ tương ứng là A1 và A2. Biết dao động tổng hợp có phương trình \(x = 16\cos \omega t\) (cm) và lệch pha so với dao động thứ nhất một góc \({\alpha _1}\) . Thay đổi biên độ của hai dao động, trong đó biên độ của dao động thứ hai tăng lên \(\sqrt {15} \) lần (nhưng vẫn giữ nguyên pha của hai dao động thành phần) khi đó dao động tổng hợp có biên độ không đổi nhưng lệch pha so với dao động thứ nhất một góc \({\alpha _2}\) , với \({\alpha _1} + {\alpha _2} = \frac{\pi }{2}\) . Giá trị ban đầu của biên độ A2 là
A. 4 cm
B. 13 cm
C. 9 cm
D. 6 cm

 

[Tăng Giáp]

Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương cùng tần số có các phương trình là x1 = 4cos(10t + π/4) cm; x2 = 3cos(10t + 3π/4) cm. Gia tốc cực đại của vật trong quá trình dao động là
A. 5m/s2.
B. 50 cm/s2.
C. 0,5 m/s2.
D. 5 cm/s2.

 

[Tăng Giáp]

Hai chất điểm M, N dao động điều hòa cùng tần số dọc theo hai đường thẳng song song kề nhau và song song với trục Ox. Vị trí cân bằng của M và N đều nằm trên một đường thẳng qua gốc tọa độ và vuông góc với trục Ox. Trong quá trình dao động, hình chiếu của M và N trên Ox cách xa nhau nhất là \(\sqrt 2 \)cm. Biên độ dao động tổng hợp của M và N là 2 cm. Gọi A$_M$, A$_N$ lần lượt là biên độ của M và N. Giá trị lớn nhất của (A$_M$ + A$_N$) gần với giá trị nào nhất sau đây?
A. 3 cm.
B. 4 cm.
C. 5 cm.
D. 6 cm.

 

[Tăng Giáp]

Một chất điểm thực hiện đồng thời hai dao động điều hòa cùng phương cùng tần số . Nếu hai dao động thành phần lệch pha nhau \(\frac{{\rm{\pi }}}{{\rm{2}}}\) thì biên độ dao động tổng hợp là 20 cm. Nếu hai dao động thành phần ngược pha thì biên độ dao động tổng hợp là 15,6 cm. Biết biên độ của dao động thành phần thứ nhất lớn hơn so với biên độ của dao động thành phần thứ 2. Hỏi nếu hai dao động thành phần trên cùng pha với nhau thì biên độ dao động tổng hợp có giá trị gần giá trị nào nhất sau đây?
A. 21,2 cm.
B. 27,5 cm
C. 23,9 cm
D. 25,4 cm.

 

[Tăng Giáp]

Một vật tham gia đồng thời vào hai dao động điều hòa cùng phương, cùng tần số, cùng pha với biên độ lần lượt là \({A_1} = 4cm\) và \({A_2} = 6cm\) . Dao động tổng hợp có biên độ bằng
A. \(A = 10cm\)
B. \(A = 2\sqrt {13} cm\)
C. \(A = 2\sqrt 5 cm\)
D. \(A = 2cm\)

 

[Tăng Giáp]

Hai dao động điều hòa cùng phương, có phương trình lần lượt \({x_1} = {A_1}\cos \left( {\omega t - \frac{\pi }{6}} \right)\) cm và \({x_2} = {A_2}\cos \left( {\omega t - \pi } \right)\) cm. Phương trình dao động tổng hợp là \(x = 9\cos \left( {\omega t + \varphi } \right)\) cm. Để biên độ A2 có giá trị cực đại thì biên độ A1 gần nhất với giá trị nào sau đây?
A. 20 cm
B. 9 cm
C. 18 cm
D. 16 cm

 

[Tăng Giáp]

Một chất điểm có khối lượng đồng thời thực hiện hai dao động điều hòa cùng phương, cùng tần số. Ở thời điểm t bất kì li độ của hai dao động thành phần luôn thõa mãn \(16{\rm{x}}_1^2 + 9{\rm{x}}_2^2 = 25\) (x1, x2 tính bằng cm). Biết lực phục hồi cực đại tác dụng lên chất điểm trong quá trình dao động là \({F_{ma{\rm{x}}}} = 0,4N\) . Tần số góc của đao động có giá trị
A. 10π rad/s
B. 8π rad/s
C. 4 rad/s
D. 4π rad/s

 

[dangtuan181114]

Vì sao nên lựa chọn mua bàn thờ gia tiên bằng gỗ mít?

Từ thời cha ông ta từ xưa các loại gỗ tự nhiên được người dân Việt ưa chuộng hơn cả vì khi được sơn bóng, nó đảm bảo được độ bền và đáp ứng được về mặt thẩm mỹ, đặc biệt chất liệu gỗ mít được nhiều người dân tin dùng.

Phòng thờ gia tiên từ xa xưa đến ngày nay luôn luôn được coi là nơi tôn kính cần được thiết kế sao cho phù hợp, tuyệt đối không dùng mua bàn thờ gia tiên các loại ánh kim: Sắt, thép, inox hay nhôm kính bởi chúng tạo ra các trường khí không tốt đồng thời không hợp mỹ quan người nhìn.

Bởi vậy, bàn thờ gia tiên luôn phải được làm từ gỗ tự nhiên, có độ bền cao, đẹp. Người ta thường chọn các loại gỗ quý: Đinh, lim,… để làm bàn thờ, trong đó chắc chắn chúng ta không thể không nhắc tới bàn thờ gia tiên làm bằng gỗ mít. Vậy loại gỗ này có những ưu điểm nổi bật gì mà thường được làm bàn thờ gia tiên đến vậy? Xin mời quý bạn đọc cùng với ANAMO tìm hiểu về loại bàn thờ làm bằng gỗ đặc biệt này nhé !

3 ưu điểm của bàn thờ gia tiên làm bằng gỗ mít

Từ xa xưa, ông cha ta đã sử dụng cây gỗ mít ứng dụng trong việc làm các đồ thờ như tủ thờ, bàn thờ, hoành phi câu đối, làm các đồ thờ cúng trong đình, chùa…Đây là cây gỗ có tính chất ổn định, không hề bị cong vênh hay bị mối mọt phá loại. Gỗ mít có màu sắc sáng, khi để lâu sẽ có màu đỏ sẫm với mùi thơm dịu nhẹ, gỗ lại mềm, dẻo. Vì thế nó được dùng phổ biến trong việc tạc đồ thờ cúng.Với bàn tay khéo léo của các nghệ nhân, từ chất liệu gỗ mít đã tạo nên những sản phẩm gỗ mít độc đáo, đặc biệt là sản phẩm bàn thờ gỗ mít với nhiều mẫu mã và kiểu dáng phù hợp với nhiều kiến trúc ngôi nhà, có giá trị tâm linh rất lớn.



Cứ mỗi độ Tết đến Xuân về, gia đình nào cũng có mâm ngũ quả dâng lên bàn thờ tổ tiên, ông bà. Mâm ngũ quả bên cành đào, câu đối đỏ, bức tranh tết, bánh chưng xanh… tạo nên khung cảnh ấm áp của mỗi gia đình khi tết đến xuân về. Ở thời điểm này thì bàn thờ sẽ là nơi linh thiêng nhất trong mỗi gia đình thể hiện lòng thành kính của con cháu đối với tổ tiên.

Không chỉ dịp Tết mà vào các ngày rằm, mùng 1 hay giỗ chạp… thì phòng thờ luôn là một không gian quan trọng có ý nghĩa rất lớn trong đời sống tinh thần của con người. Việc đặt ban thờ theo phong thủy như thế nào, đặt ban thờ theo tuổi, bố trí bàn thờ tủ thờ ra sao, xem hướng đặt ban thờ, chọn hướng đặt ban thờ ra sao chắc vẫn là những câu hỏi mà nhiều người đang băn khoăn? Tất cả các câu hỏi này sẽ được Banthogiatien.net chúng tôi giải đáp nhanh chóng bằng các bài viết liên quan đến việc xem phong thủy, hướng đặt bàn thờ, bố trí bàn thờ tủ thờ gia đình …tất cả sẽ có trong Banthogiatien.net

Ngoài ra Banthogiatien.net chúng tôi chuyên cung cấp, buôn bán các mẫu đồ thờ, bàn thờ gia tiên đẹp, hiện đại, trang nhã, được thiết kế từ những loại gỗ quý nhất từ nhất thợ chuyên nghiệp. Với kiến trúc thiết kế và sản xuất đa dạng của Banthogiatien.net chắc chắn sẽ mang lại cho các bạn nhiều sự lựa chọn cũng như tìm gia giải pháp cho gia đình bạn.



Trong văn hoá thờ cúng của người Việt là một điều tâm linh và thiêng liêng thể hiện tình cảm sự biết ơn đến những đấng sinh thành, những người có công với đất nước cũng như với nhiều người của đất nước. Chính vì điều đó lựa chọn mẫu bàn thờ gia tiên là việc đầu tiên bạn cần quan tâm, thể hiện sự đẹp đẽ, trang nghiêm và hài hoà với tổng thể của căn hộ. Hãy lựa chọn một mẫu bàn thờ vừa với các đồ đạc và phong cách, lối sống sinh hoạt của gia đình gia chủ.