Nguyễn Vũ Hồng Trang
Mới đăng kí
Chỉnh sửa cuối:
2 bai tap
- Thread starter Nguyễn Vũ Hồng Trang
- Ngày gửi
Thái
Mới đăng kí
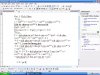
Phương trình hoành độ giao điểm của (C) và (d):
$\begin{array}{l}\;\;\;\;\;\frac{{x + 3}}{{ - x + 2}}\; = x - m - 1\\ \Leftrightarrow {x^2} - (m + 2)x + 2m + 5 = 0\;\;(1)\;(x \ne 2)\;\end{array}$
Điều kiện:
$\left\{ \begin{array}{l}\Delta = {(m + 2)^2} - 4(2m + 5) = {m^2} - 4m - 16 > 0\\{2^2} - 2(m + 2) + 2m + 5 \ne 0\\{0^2} - (m + 2).0 + 2m + 5 \ne 0\end{array} \right.\;\;(*)$
Với điều kiện (*) phương trình (1) luôn có hai nghiệm phân biệt ${x_1};{x_2}$ và khác 2 và khác 0, hay (d) cắt (C) tại hai điểm phân biệt $A({x_1};{x_1} - m - 1);B({x_2};{x_2} - m - 1)$, không trùng điểm O.
Ta có $\overrightarrow {OA} = ({x_1};{x_1} - m - 1);\overrightarrow {OB} = ({x_2};{x_2} - m - 1)$. Vì tam giác OAB vuông tại O nên $\overrightarrow {OA} .\overrightarrow {OB} = 0 \Leftrightarrow {x_1}{x_2} + ({x_1} - m - 1)({x_1} - m - 1) = 0 \Leftrightarrow 2{x_1}{x_2} - (m + 1)({x_1} + {x_2}) + {(m + 1)^2} = 0\;\;(**)$
Theo định lí Viet ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} = m + 2\\{x_1}{x_2} = 2m + 5\end{array} \right.$, thay vào (**) được: $2(2m + 5) - (m + 1)(m + 2) + {(m + 1)^2} = 0\; \Leftrightarrow m = - 3.$
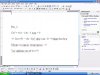
$\begin{array}{l}\;\;\;\;\;\frac{{x + 3}}{{ - x + 2}}\; = x - m - 1\\ \Leftrightarrow {x^2} - (m + 2)x + 2m + 5 = 0\;\;(1)\;(x \ne 2)\;\end{array}$
Điều kiện:
$\left\{ \begin{array}{l}\Delta = {(m + 2)^2} - 4(2m + 5) = {m^2} - 4m - 16 > 0\\{2^2} - 2(m + 2) + 2m + 5 \ne 0\\{0^2} - (m + 2).0 + 2m + 5 \ne 0\end{array} \right.\;\;(*)$
Với điều kiện (*) phương trình (1) luôn có hai nghiệm phân biệt ${x_1};{x_2}$ và khác 2 và khác 0, hay (d) cắt (C) tại hai điểm phân biệt $A({x_1};{x_1} - m - 1);B({x_2};{x_2} - m - 1)$, không trùng điểm O.
Ta có $\overrightarrow {OA} = ({x_1};{x_1} - m - 1);\overrightarrow {OB} = ({x_2};{x_2} - m - 1)$. Vì tam giác OAB vuông tại O nên $\overrightarrow {OA} .\overrightarrow {OB} = 0 \Leftrightarrow {x_1}{x_2} + ({x_1} - m - 1)({x_1} - m - 1) = 0 \Leftrightarrow 2{x_1}{x_2} - (m + 1)({x_1} + {x_2}) + {(m + 1)^2} = 0\;\;(**)$
Theo định lí Viet ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} = m + 2\\{x_1}{x_2} = 2m + 5\end{array} \right.$, thay vào (**) được: $2(2m + 5) - (m + 1)(m + 2) + {(m + 1)^2} = 0\; \Leftrightarrow m = - 3.$
