Đề khảo sát chất lượng Toán 12 lần 2 năm 2024-2025 do Sở GD&ĐT Thanh Hóa tổ chức đang thu hút sự quan tâm đặc biệt từ học sinh và giáo viên trên toàn tỉnh. Đây không chỉ là dịp để các em học sinh lớp 12 đánh giá lại kiến thức và kỹ năng sau một thời gian ôn luyện, mà còn là cơ sở quan trọng giúp giáo viên điều chỉnh phương pháp giảng dạy, chuẩn bị tốt cho kỳ thi tốt nghiệp THPT sắp tới. Đề khảo sát chất lượng Toán 12 lần 2 năm nay được đánh giá là bám sát cấu trúc đề thi minh họa của Bộ GD&ĐT, có sự phân hóa rõ ràng, giúp phân loại năng lực học sinh hiệu quả. Với nội dung cập nhật, bố cục chặt chẽ và mức độ câu hỏi hợp lý, đề thi của Sở GD&ĐT Thanh Hóa là tài liệu tham khảo hữu ích cho học sinh lớp 12 trên cả nước trong quá trình ôn luyện.

Câu 1. Trong không gian Oxyz, cho mặt cầu (S) có phương trình $(x - 1)^2 + (y + 4)^2 + z^2 = 9$. Đường kính của mặt cầu (S) bằng
A. 9
B. 18
C. 6
D. 3.
Câu 2. Cho hàm số $f(x) = ax^3 + bx^2 + cx + d$ có đồ thị như hình bên và $a, b, c, d$ là các số thực.
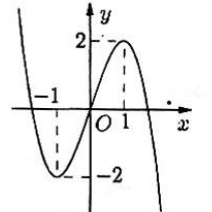
Khẳng định nào sau đây là khẳng định đúng?
A. $a + d > 0$.
B. $a + d < 0$.
C. $ad > 0$.
D. $ad < 0$.
Câu 3. Tập nghiệm của bất phương trình ${2^{3x - 7}} < 4$ là
A. $(-\infty;1)$.
B. $(3; +\infty)$.
C. $(0; +\infty)$.
D. $(-\infty;3)$.
Câu 4. Trong không gian $Oxyz$, khoảng cách từ điểm $A(1;3;-2)$ đến mặt phẳng $(Oxy)$ bằng
A. 2.
B. $\sqrt{14}$.
C. 3.
D. 1.
Câu 5. Cho hàm số $f(x) = x^2 + 4$. Khẳng định nào dưới đây đúng?
A. $\int f(x)\,dx = x^2 + 4x + C$.
B. $\int f(x)\,dx = \dfrac{x^2}{3} + 4x + C$.
C. $\int f(x)\,dx = x^3 + 4x + C$.
D. $\int f(x)\,dx = 2x + C$.
Câu 6. Cho cấp số nhân $(u_n)$ với $u_1 = 3$ và $u_4 = 81$. Công bội của cấp số nhân đã cho bằng
A. $3\sqrt{3}$.
B. $3\sqrt[3]{3}.$
C. $3\sqrt{5}$.
D. 3.
Câu 7. Khảo sát thu nhập theo tháng của người lao động ở một công ty thu được mẫu số ghép nhóm như bảng sau:
Tính mức thu nhập trung bình của người lao động ở công ty trên (đơn vị: triệu đồng)
A. 12,5.
B. 11,75.
C. 11.
D. 10,5.
Câu 8. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành và $M$ là trung điểm của $CD$. Phát biểu nào sau đây là đúng?
A. $\overrightarrow{SM} = \dfrac{1}{2}(\overrightarrow{SA} + \overrightarrow{SB} + 2\overrightarrow{SC})$.
B. $\overrightarrow{SM} = \dfrac{1}{2}(\overrightarrow{SA} - \overrightarrow{SB} + 2\overrightarrow{SC})$.
C. $\overrightarrow{SM} = \dfrac{1}{2}(\overrightarrow{SA} + \overrightarrow{SB} + \overrightarrow{SC})$.
D. $\overrightarrow{SM} = \dfrac{1}{2}(\overrightarrow{SA} - \overrightarrow{SB} - 2\overrightarrow{SC})$.
Câu 9. Cho hình chóp $S.ABC$ có đáy là tam giác đều và $SA \perp (ABC)$. Gọi $H$ là hình chiếu vuông góc của $S$ lên $BC$. Khẳng định nào sau đây là khẳng định đúng?
A. $BC \perp SB$.
B. $BC \perp SC$.
C. $BC \perp AH$.
D. $BC \perp AC$.
Câu 10. Nếu $\int_{ - 2}^1 f (x){\mkern 1mu} dx = 6$ thì $\int_{ - 2}^1 {\left[ {2 + f\left( x \right)} \right]} {\mkern 1mu} dx$ bằng
A. 12.
B. 10.
C. 0.
D. 6.
Câu 11. Cho hàm số $f(x)$ có bảng biến thiên như sau:
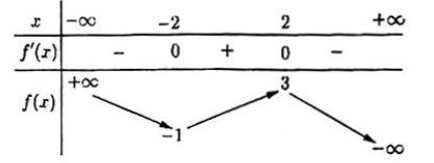
Giá trị cực đại của hàm số đã cho bằng
A. 3.
B. –2.
C. –1.
D. 2.
Câu 12. Số nghiệm thuộc đoạn $[-π;π]$ của phương trình $\sin 2x - 1 = 0$ là
A. 1
B. 2
C. 3
D. 4
Câu 1. Trong không gian $Oxyz$, cho điểm $A(6;-10;3)$, mặt cầu $(S)$ có tâm $I(0;2;-3)$, bán kính bằng $2\sqrt{6}$ và mặt phẳng $(\alpha)$ có phương trình $x + y = 0$.
a) Điểm $A$ nằm ngoài mặt cầu $(S)$.
b) Hình chiếu của điểm $A$ lên mặt phẳng $(\alpha)$ là điểm $Q(8;-8;3)$.
c) Khoảng cách từ điểm $I$ đến mặt phẳng $(\alpha)$ bằng 2.
d) Mặt phẳng $(\alpha)$ cắt mặt cầu $(S)$ theo đường tròn $(C)$. Điểm $M$ thuộc đường tròn $(C)$ sao cho khoảng cách từ $M$ đến $A$ lớn nhất. Khi đó $MA = 6\sqrt{10}$.
Câu 2. Thành nhà Hồ nằm trên địa phận huyện Vĩnh Lộc, tỉnh Thanh Hóa được UNESCO công nhận là di sản văn hóa thế giới vào ngày 27/6/2011. Thành có bốn cổng xây bằng đá ở bốn phía Nam-Bắc-Tây-Đông (Tiền-Hậu-Tả-Hữu), trong đó phía Nam gồm 3 cửa (như hình bên), mỗi phía còn lại chỉ có một cửa, các cửa thành được xây kiểu vòm cuốn.

Trong một buổi trải nghiệm, một nhóm học sinh thực nghiệm đo đạc cửa chính giữa cửa cổng phía Nam để tính diện tích phần cửa gỗ và thu được các kết quả sau:
Bệ rộng của cửa dưới mặt đất là 5,82m, hai bên mép cửa (coi như vuông góc với mặt đất) có độ cao 2,25m. Vòm cửa cong theo dạng một cung Parabol có đỉnh là đỉnh cửa. Chiều cao từ mặt đất đến mặt trên của thành là 9,5m, khoảng cách từ đỉnh cửa đến mặt trên của thành là 3,75m. Nhóm học sinh chọn hệ trục tọa độ Oxy sao cho gốc tọa độ là điểm chính giữa đoạn thẳng nối hai chân cửa, trục Ox đi qua hai chân cửa, tia Oy hướng lên trên và đi qua đỉnh cửa, đơn vị trên mỗi trục tọa độ là 1 mét.
a) Chiều cao từ mặt đất đến đỉnh cửa là 5,75m.
b) Với hệ trục tọa độ Oxy đã chọn, đỉnh cửa là điểm I(0; 3,75).
c) Với hệ trục tọa độ Oxy đã chọn, vòm cửa là một phần của đồ thị hàm số $y = \frac{-7}{5,82}x^2 + 5,75.$
d) Trước đây, ở mỗi cửa có cánh cửa làm bằng gỗ, khi khép lại thì cửa được đóng kín. Diện tích cửa gỗ của cửa chính giữa là 26,68 m² (kết quả làm tròn đến hàng phần trăm của đơn vị m²).
Câu 3. Cho hàm số $y = f(x) = \log_3(5x - 3)$.
a) Tập xác định của hàm số $y = f(x)$ là $D = (0; +\infty)$.
b) Hàm số $y = f(x)$ đồng biến trên $\left(\dfrac{3}{5}; +\infty \right)$.
c) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = f(x)$ trên $\left[\dfrac{6}{5}; \dfrac{12}{5} \right]$ là 12.
d) Đồ thị hàm số $y = f(x)$ đi qua điểm $M(2; 7)$.
Câu 4. Gia đình bạn An chuẩn bị đi tham quan một hòn đảo trong hai ngày thứ bảy và chủ nhật. Ở hòn đảo đó, mỗi ngày chỉ có nắng hoặc mưa, nếu một ngày là nắng thì khả năng xảy ra mưa ở ngày tiếp theo là 20%, còn nếu một ngày là mưa thì khả năng ngày hôm sau vẫn mưa là 30%. Theo dự báo thời tiết, xác suất trời sẽ nắng vào ngày thứ bảy là 0,7.
Gọi $A$ là biến cố: “Ngày thứ bảy trời nắng” và $B$ là biến cố: “Ngày chủ nhật trời mưa”.
a) $P(A) = 0{,}7$.
b) $P(AB) = 0{,}21$.
c) $P\left(\overline{B} \mid A \right) = 0{,}7$.
d) Xác suất để ngày chủ nhật trời nắng là 0,8.
Câu 1. Trên cánh cửa được trang trí các núm có dạng một khối tròn xoay được đúc bằng chất liệu đồng, khuôn đúc của nó được tạo thành khi quay miền $(H)$ (phần được tô màu trong hình vẽ bên) quanh trục $AB$. Miền $(H)$ được giới hạn bởi các cạnh $AB, AD$ của hình vuông $ABCD$ và các cung phân tư của các đường tròn bán kính bằng 1 cm với tâm lần lượt là trung điểm của các cạnh $AD, AB$.
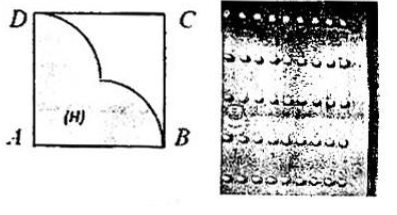
Biết công thức tính khối lượng của một vật là $P = V.D$, trong đó $P$ là khối lượng của vật (đơn vị g), $V$ là thể tích của vật (đơn vị $cm^3$) và $D$ là khối lượng riêng của vật (đơn vị $g/cm^3$), khối lượng riêng của đồng là $D = 8,96g/cm^3$. Giá đồng trên thị trường là 200.000đ/kg. Giá tiền vật liệu để đúc một núm đồng trên là bao nhiêu nghìn đồng? (Kết quả làm tròn đến hàng đơn vị).
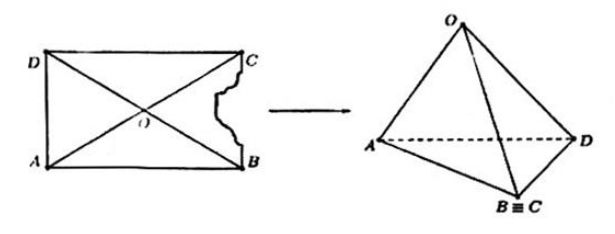
Câu 2. Trên công trường xây dựng, một công nhân muốn tạo ra một dụng cụ để đựng vật liệu lỏng từ một tấm thép hình chữ nhật $ABCD$ tâm $O$ có $AB = 3,2m, AD = 2,4m$. Do tấm thép bị hỏng một phần (tham khảo hình vẽ) nên người đó cắt bỏ tam giác $OBC$ và hàn hai mép $OB, OC$ với nhau để thu được một hình tứ diện $OABD$ (không có mặt $ABD$). Dụng cụ này sẽ được vùi đất xung quanh sao cho đỉnh $O$ quay xuống và mặt $ABD$ hướng lên trên, khi đựng đầy vật liệu lỏng thì phần không gian trong lòng của dụng cụ hoàn toàn bị lấp đầy. Tính thể tích của vật liệu lỏng được đựng đầy trong dụng cụ. (Kết quả làm tròn đến hàng phần chục của đơn vị $m^3$ và xem độ dày của tấm thép không đáng kể).
Câu 3. Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hoá bằng hàm số $N(t) = -t^2 + 24t, \, 0 \le t \le 24,$ trong đó $N$ là số người bị nhiễm bệnh và $t$ là thời gian (tuần). Số người tối đa bị nhiễm bệnh ở địa phương đó là bao nhiêu người?
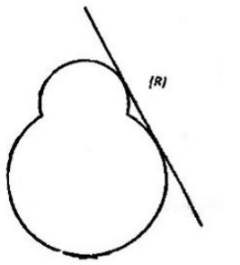
Câu 4. Ở trung tâm nghiên cứu X có một thiết bị được đặt trên một quả đồi thuộc vùng rừng núi để đo các thông số về thời tiết khí tượng của vùng đó (nhiệt độ, áp suất khí quyển, độ ẩm, mây, gió, mưa...). Cấu tạo bên ngoài của thiết bị gồm hai mặt cầu cắt nhau là $(S_1)$ có tâm $I$, bán kính bằng $4m$ và mặt cầu $(S_2)$ có tâm $J$, bán kính bằng $2m$. Để đo các thông số cần thiết, người ta lắp đặt một tấm thiết bị điện tử hình chữ nhật $(R)$ luôn tiếp xúc với cả hai mặt cầu $(S_1), (S_2)$ và có thể di chuyển quanh các chỏm cầu để truyền tín hiệu tới hộp điều hành (đường truyền không dây). Chọn hệ trục tọa độ $Oxyz$ trong không gian với độ dài đơn vị trên mỗi trục tọa độ là $1m$ và $O(0;0;0)$ là vị trí hộp điều hành thiết bị thì $I(2;1;1)$ và $J(2;1;5)$. Khi khoảng cách từ $O$ đến tấm thiết bị điện tử $(R)$ ngắn nhất là lúc đường truyền tín hiệu tốt nhất. Khoảng cách ngắn nhất này bằng bao nhiêu mét? (Kết quả làm tròn đến hàng phần trăm, tham khảo mô tả thiết bị như hình trên).
Câu 5. Một nhóm sinh viên y khoa thực hiện khảo sát những bệnh nhân bị tai nạn xe máy về mối liên hệ giữa việc đội mũ bảo hiểm và khả năng bị chấn thương vùng đầu cho thấy: Tỉ lệ bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn là 70%; tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách khi gặp tai nạn là 90%; tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách bị chấn thương vùng đầu là 21%. Hỏi theo kết quả khảo sát trên, việc đội mũ bảo hiểm đúng cách sẽ làm giảm khả năng bị chấn thương vùng đầu bao nhiêu lần?
Câu 6. Một xưởng cơ khí sản xuất hai loại sản phẩm là A và B. Để sản xuất một sản phẩm A phải dùng máy I trong 1 giờ và máy II trong 3 giờ, đối với một sản phẩm B phải dùng máy I trong 2 giờ và máy II trong 2 giờ. Mỗi tuần máy I làm việc tối đa 40 giờ, máy II làm việc tối đa 60 giờ. Mỗi sản phẩm A cho lợi nhuận 2 triệu đồng, mỗi sản phẩm B cho lợi nhuận 1,5 triệu đồng. Biết rằng sản phẩm sản xuất ra đều bán hết. Hỏi mỗi tuần xưởng cơ khí thu được lợi nhuận cao nhất là bao nhiêu triệu đồng?

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.Câu 1. Trong không gian Oxyz, cho mặt cầu (S) có phương trình $(x - 1)^2 + (y + 4)^2 + z^2 = 9$. Đường kính của mặt cầu (S) bằng
A. 9
B. 18
C. 6
D. 3.
Câu 2. Cho hàm số $f(x) = ax^3 + bx^2 + cx + d$ có đồ thị như hình bên và $a, b, c, d$ là các số thực.

Khẳng định nào sau đây là khẳng định đúng?
A. $a + d > 0$.
B. $a + d < 0$.
C. $ad > 0$.
D. $ad < 0$.
Câu 3. Tập nghiệm của bất phương trình ${2^{3x - 7}} < 4$ là
A. $(-\infty;1)$.
B. $(3; +\infty)$.
C. $(0; +\infty)$.
D. $(-\infty;3)$.
Câu 4. Trong không gian $Oxyz$, khoảng cách từ điểm $A(1;3;-2)$ đến mặt phẳng $(Oxy)$ bằng
A. 2.
B. $\sqrt{14}$.
C. 3.
D. 1.
Câu 5. Cho hàm số $f(x) = x^2 + 4$. Khẳng định nào dưới đây đúng?
A. $\int f(x)\,dx = x^2 + 4x + C$.
B. $\int f(x)\,dx = \dfrac{x^2}{3} + 4x + C$.
C. $\int f(x)\,dx = x^3 + 4x + C$.
D. $\int f(x)\,dx = 2x + C$.
Câu 6. Cho cấp số nhân $(u_n)$ với $u_1 = 3$ và $u_4 = 81$. Công bội của cấp số nhân đã cho bằng
A. $3\sqrt{3}$.
B. $3\sqrt[3]{3}.$
C. $3\sqrt{5}$.
D. 3.
Câu 7. Khảo sát thu nhập theo tháng của người lao động ở một công ty thu được mẫu số ghép nhóm như bảng sau:
| Thu nhập (Triệu đồng) | [5; 8) | [8; 11) | [11; 14) | [14; 17) | [17; 20) |
|---|---|---|---|---|---|
| Số người | 30 | 55 | 45 | 30 | 20 |
A. 12,5.
B. 11,75.
C. 11.
D. 10,5.
Câu 8. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành và $M$ là trung điểm của $CD$. Phát biểu nào sau đây là đúng?
A. $\overrightarrow{SM} = \dfrac{1}{2}(\overrightarrow{SA} + \overrightarrow{SB} + 2\overrightarrow{SC})$.
B. $\overrightarrow{SM} = \dfrac{1}{2}(\overrightarrow{SA} - \overrightarrow{SB} + 2\overrightarrow{SC})$.
C. $\overrightarrow{SM} = \dfrac{1}{2}(\overrightarrow{SA} + \overrightarrow{SB} + \overrightarrow{SC})$.
D. $\overrightarrow{SM} = \dfrac{1}{2}(\overrightarrow{SA} - \overrightarrow{SB} - 2\overrightarrow{SC})$.
Câu 9. Cho hình chóp $S.ABC$ có đáy là tam giác đều và $SA \perp (ABC)$. Gọi $H$ là hình chiếu vuông góc của $S$ lên $BC$. Khẳng định nào sau đây là khẳng định đúng?
A. $BC \perp SB$.
B. $BC \perp SC$.
C. $BC \perp AH$.
D. $BC \perp AC$.
Câu 10. Nếu $\int_{ - 2}^1 f (x){\mkern 1mu} dx = 6$ thì $\int_{ - 2}^1 {\left[ {2 + f\left( x \right)} \right]} {\mkern 1mu} dx$ bằng
A. 12.
B. 10.
C. 0.
D. 6.
Câu 11. Cho hàm số $f(x)$ có bảng biến thiên như sau:

Giá trị cực đại của hàm số đã cho bằng
A. 3.
B. –2.
C. –1.
D. 2.
Câu 12. Số nghiệm thuộc đoạn $[-π;π]$ của phương trình $\sin 2x - 1 = 0$ là
A. 1
B. 2
C. 3
D. 4
PHẦN II. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.Câu 1. Trong không gian $Oxyz$, cho điểm $A(6;-10;3)$, mặt cầu $(S)$ có tâm $I(0;2;-3)$, bán kính bằng $2\sqrt{6}$ và mặt phẳng $(\alpha)$ có phương trình $x + y = 0$.
a) Điểm $A$ nằm ngoài mặt cầu $(S)$.
b) Hình chiếu của điểm $A$ lên mặt phẳng $(\alpha)$ là điểm $Q(8;-8;3)$.
c) Khoảng cách từ điểm $I$ đến mặt phẳng $(\alpha)$ bằng 2.
d) Mặt phẳng $(\alpha)$ cắt mặt cầu $(S)$ theo đường tròn $(C)$. Điểm $M$ thuộc đường tròn $(C)$ sao cho khoảng cách từ $M$ đến $A$ lớn nhất. Khi đó $MA = 6\sqrt{10}$.
Câu 2. Thành nhà Hồ nằm trên địa phận huyện Vĩnh Lộc, tỉnh Thanh Hóa được UNESCO công nhận là di sản văn hóa thế giới vào ngày 27/6/2011. Thành có bốn cổng xây bằng đá ở bốn phía Nam-Bắc-Tây-Đông (Tiền-Hậu-Tả-Hữu), trong đó phía Nam gồm 3 cửa (như hình bên), mỗi phía còn lại chỉ có một cửa, các cửa thành được xây kiểu vòm cuốn.

Trong một buổi trải nghiệm, một nhóm học sinh thực nghiệm đo đạc cửa chính giữa cửa cổng phía Nam để tính diện tích phần cửa gỗ và thu được các kết quả sau:
Bệ rộng của cửa dưới mặt đất là 5,82m, hai bên mép cửa (coi như vuông góc với mặt đất) có độ cao 2,25m. Vòm cửa cong theo dạng một cung Parabol có đỉnh là đỉnh cửa. Chiều cao từ mặt đất đến mặt trên của thành là 9,5m, khoảng cách từ đỉnh cửa đến mặt trên của thành là 3,75m. Nhóm học sinh chọn hệ trục tọa độ Oxy sao cho gốc tọa độ là điểm chính giữa đoạn thẳng nối hai chân cửa, trục Ox đi qua hai chân cửa, tia Oy hướng lên trên và đi qua đỉnh cửa, đơn vị trên mỗi trục tọa độ là 1 mét.
a) Chiều cao từ mặt đất đến đỉnh cửa là 5,75m.
b) Với hệ trục tọa độ Oxy đã chọn, đỉnh cửa là điểm I(0; 3,75).
c) Với hệ trục tọa độ Oxy đã chọn, vòm cửa là một phần của đồ thị hàm số $y = \frac{-7}{5,82}x^2 + 5,75.$
d) Trước đây, ở mỗi cửa có cánh cửa làm bằng gỗ, khi khép lại thì cửa được đóng kín. Diện tích cửa gỗ của cửa chính giữa là 26,68 m² (kết quả làm tròn đến hàng phần trăm của đơn vị m²).
Câu 3. Cho hàm số $y = f(x) = \log_3(5x - 3)$.
a) Tập xác định của hàm số $y = f(x)$ là $D = (0; +\infty)$.
b) Hàm số $y = f(x)$ đồng biến trên $\left(\dfrac{3}{5}; +\infty \right)$.
c) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = f(x)$ trên $\left[\dfrac{6}{5}; \dfrac{12}{5} \right]$ là 12.
d) Đồ thị hàm số $y = f(x)$ đi qua điểm $M(2; 7)$.
Câu 4. Gia đình bạn An chuẩn bị đi tham quan một hòn đảo trong hai ngày thứ bảy và chủ nhật. Ở hòn đảo đó, mỗi ngày chỉ có nắng hoặc mưa, nếu một ngày là nắng thì khả năng xảy ra mưa ở ngày tiếp theo là 20%, còn nếu một ngày là mưa thì khả năng ngày hôm sau vẫn mưa là 30%. Theo dự báo thời tiết, xác suất trời sẽ nắng vào ngày thứ bảy là 0,7.
Gọi $A$ là biến cố: “Ngày thứ bảy trời nắng” và $B$ là biến cố: “Ngày chủ nhật trời mưa”.
a) $P(A) = 0{,}7$.
b) $P(AB) = 0{,}21$.
c) $P\left(\overline{B} \mid A \right) = 0{,}7$.
d) Xác suất để ngày chủ nhật trời nắng là 0,8.
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.Câu 1. Trên cánh cửa được trang trí các núm có dạng một khối tròn xoay được đúc bằng chất liệu đồng, khuôn đúc của nó được tạo thành khi quay miền $(H)$ (phần được tô màu trong hình vẽ bên) quanh trục $AB$. Miền $(H)$ được giới hạn bởi các cạnh $AB, AD$ của hình vuông $ABCD$ và các cung phân tư của các đường tròn bán kính bằng 1 cm với tâm lần lượt là trung điểm của các cạnh $AD, AB$.

Biết công thức tính khối lượng của một vật là $P = V.D$, trong đó $P$ là khối lượng của vật (đơn vị g), $V$ là thể tích của vật (đơn vị $cm^3$) và $D$ là khối lượng riêng của vật (đơn vị $g/cm^3$), khối lượng riêng của đồng là $D = 8,96g/cm^3$. Giá đồng trên thị trường là 200.000đ/kg. Giá tiền vật liệu để đúc một núm đồng trên là bao nhiêu nghìn đồng? (Kết quả làm tròn đến hàng đơn vị).
Câu 2. Trên công trường xây dựng, một công nhân muốn tạo ra một dụng cụ để đựng vật liệu lỏng từ một tấm thép hình chữ nhật $ABCD$ tâm $O$ có $AB = 3,2m, AD = 2,4m$. Do tấm thép bị hỏng một phần (tham khảo hình vẽ) nên người đó cắt bỏ tam giác $OBC$ và hàn hai mép $OB, OC$ với nhau để thu được một hình tứ diện $OABD$ (không có mặt $ABD$). Dụng cụ này sẽ được vùi đất xung quanh sao cho đỉnh $O$ quay xuống và mặt $ABD$ hướng lên trên, khi đựng đầy vật liệu lỏng thì phần không gian trong lòng của dụng cụ hoàn toàn bị lấp đầy. Tính thể tích của vật liệu lỏng được đựng đầy trong dụng cụ. (Kết quả làm tròn đến hàng phần chục của đơn vị $m^3$ và xem độ dày của tấm thép không đáng kể).

Câu 3. Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hoá bằng hàm số $N(t) = -t^2 + 24t, \, 0 \le t \le 24,$ trong đó $N$ là số người bị nhiễm bệnh và $t$ là thời gian (tuần). Số người tối đa bị nhiễm bệnh ở địa phương đó là bao nhiêu người?
Câu 4. Ở trung tâm nghiên cứu X có một thiết bị được đặt trên một quả đồi thuộc vùng rừng núi để đo các thông số về thời tiết khí tượng của vùng đó (nhiệt độ, áp suất khí quyển, độ ẩm, mây, gió, mưa...). Cấu tạo bên ngoài của thiết bị gồm hai mặt cầu cắt nhau là $(S_1)$ có tâm $I$, bán kính bằng $4m$ và mặt cầu $(S_2)$ có tâm $J$, bán kính bằng $2m$. Để đo các thông số cần thiết, người ta lắp đặt một tấm thiết bị điện tử hình chữ nhật $(R)$ luôn tiếp xúc với cả hai mặt cầu $(S_1), (S_2)$ và có thể di chuyển quanh các chỏm cầu để truyền tín hiệu tới hộp điều hành (đường truyền không dây). Chọn hệ trục tọa độ $Oxyz$ trong không gian với độ dài đơn vị trên mỗi trục tọa độ là $1m$ và $O(0;0;0)$ là vị trí hộp điều hành thiết bị thì $I(2;1;1)$ và $J(2;1;5)$. Khi khoảng cách từ $O$ đến tấm thiết bị điện tử $(R)$ ngắn nhất là lúc đường truyền tín hiệu tốt nhất. Khoảng cách ngắn nhất này bằng bao nhiêu mét? (Kết quả làm tròn đến hàng phần trăm, tham khảo mô tả thiết bị như hình trên).

Câu 5. Một nhóm sinh viên y khoa thực hiện khảo sát những bệnh nhân bị tai nạn xe máy về mối liên hệ giữa việc đội mũ bảo hiểm và khả năng bị chấn thương vùng đầu cho thấy: Tỉ lệ bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn là 70%; tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách khi gặp tai nạn là 90%; tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách bị chấn thương vùng đầu là 21%. Hỏi theo kết quả khảo sát trên, việc đội mũ bảo hiểm đúng cách sẽ làm giảm khả năng bị chấn thương vùng đầu bao nhiêu lần?
Câu 6. Một xưởng cơ khí sản xuất hai loại sản phẩm là A và B. Để sản xuất một sản phẩm A phải dùng máy I trong 1 giờ và máy II trong 3 giờ, đối với một sản phẩm B phải dùng máy I trong 2 giờ và máy II trong 2 giờ. Mỗi tuần máy I làm việc tối đa 40 giờ, máy II làm việc tối đa 60 giờ. Mỗi sản phẩm A cho lợi nhuận 2 triệu đồng, mỗi sản phẩm B cho lợi nhuận 1,5 triệu đồng. Biết rằng sản phẩm sản xuất ra đều bán hết. Hỏi mỗi tuần xưởng cơ khí thu được lợi nhuận cao nhất là bao nhiêu triệu đồng?
