Tải ngay Đề Thi Thử THPT 2025 Lần 1 Môn Toán - Trường THPT Chuyên Lê Khiết, Quảng Ngãi để rèn luyện kỹ năng giải toán và làm quen với cấu trúc đề thi chuẩn. Bài viết cung cấp bộ đề chi tiết với các câu hỏi từ cơ bản đến nâng cao, giúp học sinh lớp 12 ôn tập hiệu quả, tự tin chinh phục kỳ thi THPT Quốc Gia 2025 với kết quả tốt nhất!
Câu 1. Cho hình chóp \( S.ABCD \) có đáy \( ABCD \) là hình chữ nhật và \( SA \perp (ABCD) \). Đường thẳng nào sau đây vuông góc với mặt phẳng \( (SAB) \)?
A. \( SD \)
B. \( BC \)
C. \( SC \)
D. \( CD \)
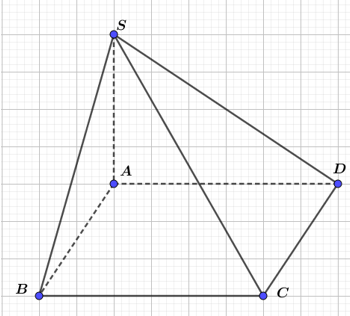
Ta có $BC\bot AB$ (gt) và $BC\bot SA\,\,\left( SA\bot \,\left( ABCD \right) \right)\Rightarrow BC\bot (SAB)$
Vậy $BC\bot (SAB)$
Câu 2. Nghiệm của phương trình \( 3^x = 6 \) là:
A. \( x = \log_3 6 \)
B. \( x = 2 \)
C. \( x = \log_6 3 \)
D. \( x = 18 \)
Câu 3. Cấp số cộng \( (u_n) \) có \( u_1 = -1 \) và \( u_2 = 3 \). Số hạng \( u_5 \) của cấp số cộng là:
A. 15
B. 5
C. 9
D. 13
Câu 4. Nguyên hàm của hàm số \( f(x) = x^2 \) là:
A. \( \dfrac{x^2}{2} + C \)
B. \( 2x + C \)
C. \( \dfrac{x^3}{3} + C \)
D. \( x^3 + C \)
Câu 5. Tập nghiệm của bất phương trình \( \log_3(x + 1) \leq 2 \) là:
A. \( (1;9) \)
B. \( (-1;7] \)
C. \( (-\infty;9] \)
D. \( (-1;8] \)
Câu 6. Cho hàm số có đồ thị như hình vẽ bên.
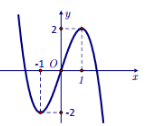
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
A. \((-1; 1)\)
B. \((-\infty; 1)\)
C. \((-\infty; -1)\)
D. \((-1; +\infty)\)
Câu 7. Cho hình hộp \( ABCD.A'B'C'D' \) (minh họa như hình bên dưới).
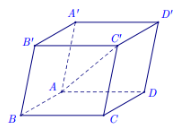
Phát biểu nào sau đây là đúng?
A. \( \overrightarrow{AB} + \overrightarrow{AC'} + \overrightarrow{AA'} = \overrightarrow{AC'} \)
B. \( \overrightarrow{AB} + \overrightarrow{BB'} + \overrightarrow{B'A'} = \overrightarrow{AC'} \)
C. \( \overrightarrow{AB} + \overrightarrow{AA'} + \overrightarrow{AD} = \overrightarrow{AC'} \)
D. \( \overrightarrow{AB} + \overrightarrow{BC'} + \overrightarrow{C'D'} = \overrightarrow{AC'} \)
Câu 8. Trong không gian với hệ trục tọa độ \( Oxyz \), phương trình của mặt phẳng đi qua gốc tọa độ \( O(0;0;0) \), có một vectơ pháp tuyến \( \vec{n}(2;0;1) \) là:
A. \( x + 2y = 0 \)
B. \( 2x + z = 0 \)
C. \( x + 2z = 0 \)
D. \( 2x + y = 0 \)
Câu 9. Cho một vật thể trong không gian \( Oxyz \). Gọi \( B \) là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục \( Ox \) tại các điểm có hoành độ \( x = a; x = b \). Một mặt phẳng vuông góc với trục \( Ox \) tại điểm có hoành độ là \( x \) cắt vật thể theo mặt cắt có diện tích là \( S(x) \). Giả sử \( S(x) \) là hàm số liên tục trên đoạn \([a; b]\). Khi đó thể tích \( V \) của phần vật thể \( B \) tính theo công thức:
A. \( V = \pi \int_a^b S(x) dx \)
B. \( V = \pi \int_a^b [S(x)]^2 dx \)
C. \( V = \int_a^b S(x) dx \)
D. \( V = \pi^2 \int_a^b S(x) dx \)
Câu 10. Cho hàm số \( y = \dfrac{2x + 3}{x + 1} \). Tiệm cận đứng của đồ thị hàm số này là:
A. \( y = \dfrac{1}{2} \)
B. \( y = -1 \)
C. \( x = \dfrac{1}{2} \)
D. \( x = -1 \)
Câu 11. Trong không gian với hệ trục tọa độ \( Oxyz \), cho mặt phẳng \( (P) \) có phương trình
\( x + y - z + 8 = 0 \). Vector nào sau đây là một vector pháp tuyến của mặt phẳng \( (P) \)?
A. \( \vec{n}_3 (1;1; - 1) \)
B. \( \vec{n}_1 (1;-1;1) \)
C. \( \vec{n}_4 (1;1;8) \)
D. \( \vec{n}_2 (1;-1;-1) \)
Câu 12. Hai mẫu số liệu ghép nhóm \( M_1, M_2 \) có bảng tần số ghép nhóm như sau:
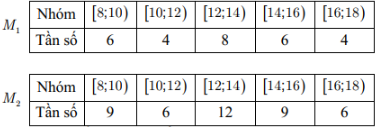
Gọi \( s_1, s_2 \) lần lượt là độ lệch chuẩn của mẫu số liệu ghép nhóm \( M_1, M_2 \). Phát biểu nào sau đây là đúng?
A. \( s_2 = 2s_1 \)
B. \( s_1 = s_2 \)
C. \( s_2 = \dfrac{3}{2}s_1 \)
D. \( s_1 = \dfrac{3}{2}s_2 \)
Câu 1. Cho hàm số \( f(x) = 2\sin x + x \).
a) \( f(0) = 0; \quad f(\pi) = \pi \).
b) Đạo hàm của hàm số đã cho là \( f'(x) = -2\cos x + 1 \).
c) Số nghiệm của phương trình \( f'(x) = 0 \) trên đoạn \([0; 3\pi]\) là 6.
d) Giá trị lớn nhất của \( f(x) \) trên đoạn \([0; \pi] \) là \( \dfrac{2\pi}{3} + \sqrt{3} \).
Câu 2. Bạn Hoàng Huy chọn ngẫu nhiên một bóng đèn led trên quầy. Trên quầy có hai loại đèn màu trắng và màu vàng có hình thức và kích thước như nhau. Trong đó màu trắng chiếm 60% . Bóng đèn màu trắng có tỉ lệ hỏng là 3%, bóng đèn màu vàng có tỉ lệ hỏng là 2%. Xác suất để bạn chọn được
a) Một bóng đèn màu vàng là 0,6.
b) Một bóng đèn không hỏng, biết nó màu trắng là 0,97.
c) Một bóng đèn không hỏng, biết nó màu vàng là 0,98
d) Một bóng đèn không hỏng là 0,974.
Câu 3. Hai phương tiện bay không người lái (drone) cùng lúc xuất phát tại cùng một địa điểm trên mặt đất. Sau một thời gian, chiếc thứ nhất đến vị trí cách điểm xuất phát về phía Nam 60m, về phía Đông 40m và cách mặt đất 50m, chiếc thứ hai đến vị trí cách điểm xuất phát về phía Bắc 40m, về phía Tây 20m và cách mặt đất 30m. Tại thời điểm đang xét thì
a) Chiếc thứ nhất cách điểm xuất phát 87,57m.
b) Chiếc thứ hai cách điểm xuất phát 53,85m.
c) Khoảng cách giữa hai chiếc drone là 118,32m.
d) Trong các vị trí trên mặt đất quan sát hai drone có một vị trí mà tổng khoảng cách từ vị trí này đến hai drone nhỏ nhất và tổng này bằng 141,42m.
Câu 4. Có một cái chòi hình “chóp cong”, trong đó mái chòi \( (H) \) có dạng hình “chóp lục giác cong đều” như hình vẽ bên dưới. Đáy của \( (H) \) là một hình lục giác đều tâm \( O \), đường chéo qua tâm \( O \) có độ dài là \( 10m \), chiều cao \( SO = 10m \) \((SO \text{ vuông góc với mặt phẳng đáy})\). Các cạnh bên của \( (H) \) là các sợi dây thép \( c_1; c_2; c_3; c_4; c_5; c_6 \), nằm trên các đường parabol có trục đối xứng song song với \( SO \).
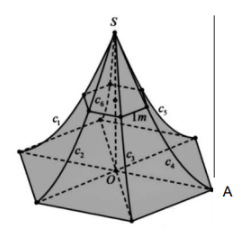
Giả sử hình tạo bởi các đoạn giao tuyến của \( (H) \) với mặt phẳng \( (\alpha) \) vuông góc với \( SO \) là một lục giác đều. Biết rằng khi mặt phẳng \( (\alpha) \) đi qua trung điểm của \( SO \) thì lục giác đều có cạnh \( l = 2(m) \).
a) Diện tích hình lục giác đều nói trên khi \( (\alpha) \) đi qua trung điểm của \( SO \) là \( 6\sqrt{3} \, (m^2) \).
b) Chọn hệ trục tọa độ \( Oxy \) sao cho gốc tọa độ là điểm \( O \) trên hình vẽ, \( S \) thuộc tia \( Oy \), đỉnh \( A \) của lục giác đều thuộc tia \( Ox \) thì \( c_4 \) nằm trên đường parabol có phương trình: $ y = \frac{1}{6}x^2 - \frac{17}{6}x + 10. $
c) Nếu \( (\alpha) \) cắt \( SO \) và \( c_4 \) lần lượt tại \( M \) và \( B \), mà \( OM = t \) thì độ dài đoạn \( BM \) là $ \frac{17}{2} - t + \sqrt{ \frac{49}{4} - t^2 }. $
d) Thể tích phần không gian nằm bên trong mái chòi \( (H) \) là \( 171{,}4 \, m^3 \).
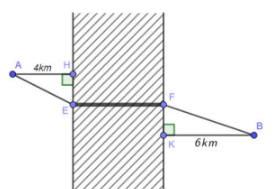
Câu 2. Hai thành phố ở hai vị trí \( A \) và \( B \) cách nhau một con sông. Người ta xây dựng một cây cầu bắc qua sông, biết rằng vị trí \( A \) cách con sông một khoảng là \( 4\,km \), vị trí \( B \) cách con sông một khoảng là \( 6\,km \) (được mô hình hóa như hình vẽ bên dưới), \( HE + KF = 20\,km \) và độ dài \( EF \) không đổi. Hỏi độ dài \( EH \) là bao nhiêu \( km \) để đường đi từ thành phố \( A \) đến thành phố \( B \) là ngắn nhất (đi theo đường \( AEFB \))?
Câu 3. Cho tập \( A = \{1;2;3;4;5;...;100\} \). Gọi \( S \) là tập các tập con của tập hợp \( A \) mà mỗi tập con này gồm 3 phần tử và có tổng 3 phần tử bằng 91. Chọn ngẫu nhiên một phần tử của tập \( S \). Khi đó, xác suất chọn được phần tử của tập \( S \) có 3 số lập thành cấp số nhân với công bội \( q \) là số nguyên dương là \( \frac{m}{n} \) (với \( m, n \) là số nguyên dương và \( \frac{m}{n} \) là phân số tối giản). Tính \( m+n \).
Câu 4. Gia đình bác An muốn làm mái tôn cho sân thượng là hình chữ nhật \( ABB'A' \) với kích thước chiều dài \( A'A' = 10m \) và chiều rộng \( AB = 6m \). Bác dự định làm mái tôn (kín) có thanh ngang \( CC' = 6m \) nằm chính giữa mái, song song và cách mặt sàn sân thượng \( 2m \) (tham khảo hình vẽ). Biết rằng chi phí làm mái tôn trọn gói cho \( 1m^2 \) là 250000 VND. Tính số tiền (triệu đồng) bác An phải chi trả (làm tròn đến hàng phần mười).
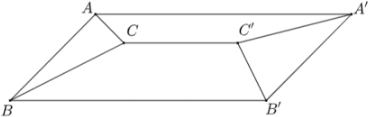
Lưu ý: Khoảng cách giữa thanh ngang và mặt sàn là độ dài đoạn thẳng nối một điểm thuộc thanh ngang đến hình chiếu của điểm đó trên mặt sàn.
Câu 5. Một tấm kính làm mặt bàn (H1) có hình dáng tam giác đều với 3 đỉnh được làm cong (H2). Biết cạnh tấm kính tam giác ban đầu bằng 16 (dm). Để cắt góc được đẹp thì người ta dùng đường Parabol (P): $ y = -\frac{\sqrt{3}}{2}x^2 + \frac{15\sqrt{3}}{2} $ (H3) có hai nhánh tiếp xúc với hai cạnh của tam giác.
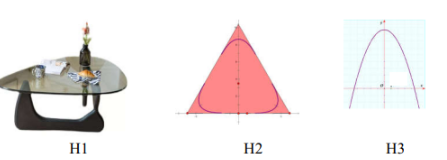
Biết diện tích mặt kính là \( a\sqrt{b} \, (dm^2) \), (với \( a \) là số nguyên dương và \( b \) là số nguyên tố). Tính \( a + b \).
Câu 6. Cho hình lăng trụ \( ABC.A'B'C' \) có đáy là tam giác đều cạnh \( 2 \, (dm) \). Hình chiếu vuông góc của điểm \( A' \) lên mặt phẳng \( (ABC) \) trùng với trọng tâm của tam giác \( ABC \). Biết khoảng cách giữa 2 đường \( AA' \) và \( BC \) bằng \( \frac{\sqrt{3}}{2} \, (dm) \). Tính thể tích \( V \, (dm^3) \) của khối lăng trụ \( ABC.A'B'C' \). (Kết quả làm tròn đến chữ số hàng phần trăm).
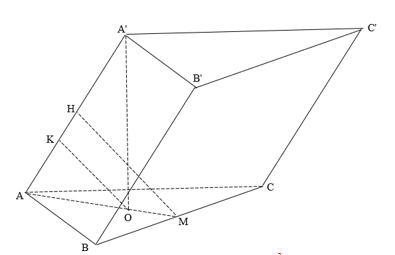
Gọi $O$ là trọng tâm của tam giác $ABC$, $M$ là trung điểm của $BC$.
Gọi $H,K$ lần lượt là hình chiếu vuông góc của $M,O$ lên $A{A}'$.
Tam giác $ABC$ đều cạnh bằng $2$ nên ${{S}_{\Delta ABC}}={{2}^{2}}.\frac{\sqrt{3}}{4}=\sqrt{3};\,\,AM=2.\frac{\sqrt{3}}{2}=\sqrt{3}$.
$AO=\frac{2}{3}AM=\frac{2\sqrt{3}}{3}$.
Ta có $MH$là đường vuông góc chung của $A{A}'$và $BC$ nên $MH=\frac{\sqrt{3}}{2}$.
$\frac{OK}{MH}=\frac{AO}{AM}=\frac{2}{3}\Rightarrow OK=\frac{2}{3}MH=\frac{2}{3}.\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3}$.
Tam giác $A{A}'O$ vuông tại $O$, nên
$\begin{array}{l} \frac{1}{{O{K^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{S^2}}}\\ \Rightarrow \frac{1}{{O{S^2}}} = \frac{1}{{O{K^2}}} - \frac{1}{{O{A^2}}}\\ = \frac{1}{{{{\left( {\frac{{\sqrt 3 }}{3}} \right)}^2}}} - \frac{1}{{{{\left( {\frac{{2\sqrt 3 }}{3}} \right)}^2}}} = \frac{9}{4}\\ \Rightarrow SO = \frac{2}{3} \end{array}$
Vậy thể tích khối lăng trụ $ABC.{A}'{B}'{C}'$ là ${{V}_{ABC.{A}'{B}'{C}'}}={{S}_{\Delta ABC}}.SO=\frac{2}{\sqrt{3}}\simeq 1,15\,\,\left( d{{m}^{3}} \right)$
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.Câu 1. Cho hình chóp \( S.ABCD \) có đáy \( ABCD \) là hình chữ nhật và \( SA \perp (ABCD) \). Đường thẳng nào sau đây vuông góc với mặt phẳng \( (SAB) \)?
A. \( SD \)
B. \( BC \)
C. \( SC \)
D. \( CD \)

Ta có $BC\bot AB$ (gt) và $BC\bot SA\,\,\left( SA\bot \,\left( ABCD \right) \right)\Rightarrow BC\bot (SAB)$
Vậy $BC\bot (SAB)$
A. \( x = \log_3 6 \)
B. \( x = 2 \)
C. \( x = \log_6 3 \)
D. \( x = 18 \)
Ta có: ${{3}^{x}}=6\Leftrightarrow x={{\log }_{3}}6$.
A. 15
B. 5
C. 9
D. 13
Ta có ${{u}_{2}}={{u}_{1}}+d\Leftrightarrow 3=-1+d\,$$\Leftrightarrow d=4$
Do đó: ${{u}_{5}}={{u}_{1}}+4d=-1+4.4=15.$
Vậy: ${{u}_{5}}=15$.
Do đó: ${{u}_{5}}={{u}_{1}}+4d=-1+4.4=15.$
Vậy: ${{u}_{5}}=15$.
A. \( \dfrac{x^2}{2} + C \)
B. \( 2x + C \)
C. \( \dfrac{x^3}{3} + C \)
D. \( x^3 + C \)
Ta có $\int{{{x}^{2}}\text{d}x}=\frac{{{x}^{3}}}{3}+C$.
A. \( (1;9) \)
B. \( (-1;7] \)
C. \( (-\infty;9] \)
D. \( (-1;8] \)
Điều kiện: $x>-1$.
Khi đó ${{\log }_{3}}\left( x+1 \right)\le 2\Leftrightarrow x+1\le 9\Leftrightarrow x\le 8$
Kết hợp điều kiện ta có $-1<x\le 8$.
Vậy tập nghiệm của bất phương trình là $\left( -1;8 \right]$.
Khi đó ${{\log }_{3}}\left( x+1 \right)\le 2\Leftrightarrow x+1\le 9\Leftrightarrow x\le 8$
Kết hợp điều kiện ta có $-1<x\le 8$.
Vậy tập nghiệm của bất phương trình là $\left( -1;8 \right]$.

Hàm số đã cho nghịch biến trên khoảng nào sau đây?
A. \((-1; 1)\)
B. \((-\infty; 1)\)
C. \((-\infty; -1)\)
D. \((-1; +\infty)\)
Dựa vào đồ thị hàm số thì hàm số đã cho nghịch biến trên khoảng $\left( -\infty ;-1 \right)$.

Phát biểu nào sau đây là đúng?
A. \( \overrightarrow{AB} + \overrightarrow{AC'} + \overrightarrow{AA'} = \overrightarrow{AC'} \)
B. \( \overrightarrow{AB} + \overrightarrow{BB'} + \overrightarrow{B'A'} = \overrightarrow{AC'} \)
C. \( \overrightarrow{AB} + \overrightarrow{AA'} + \overrightarrow{AD} = \overrightarrow{AC'} \)
D. \( \overrightarrow{AB} + \overrightarrow{BC'} + \overrightarrow{C'D'} = \overrightarrow{AC'} \)
Áp dụng quy tắc hình hộp, ta có: $\overrightarrow{A{C}'}=\overrightarrow{AB}+\overrightarrow{A{A}'}+\overrightarrow{AD}$.
A. \( x + 2y = 0 \)
B. \( 2x + z = 0 \)
C. \( x + 2z = 0 \)
D. \( 2x + y = 0 \)
Phương trình của mặt phẳng đi qua gốc tọa độ $O=\left( 0;0;0 \right)$, có một vectơ pháp tuyến và $\overrightarrow{n}=\left( 2;0;1 \right)$ là: $2x+z=0$.
A. \( V = \pi \int_a^b S(x) dx \)
B. \( V = \pi \int_a^b [S(x)]^2 dx \)
C. \( V = \int_a^b S(x) dx \)
D. \( V = \pi^2 \int_a^b S(x) dx \)
Thể tích $V$ của phần vật thể $B$ tính theo công thức $V=\int\limits_{a}^{b}{S\left( x \right)}dx$.
A. \( y = \dfrac{1}{2} \)
B. \( y = -1 \)
C. \( x = \dfrac{1}{2} \)
D. \( x = -1 \)
Tập xác định $D=\mathbb{R}\backslash \left\{ -1 \right\}$.
$\underset{x\to -{{1}^{+}}}{\mathop{\lim }}\,y=\underset{x\to -{{1}^{+}}}{\mathop{\lim }}\,\frac{2x+3}{x+1}=+\infty $ và $\underset{x\to -{{1}^{-}}}{\mathop{\lim }}\,y=\underset{x\to -{{1}^{-}}}{\mathop{\lim }}\,\frac{2x+3}{x+1}=-\infty $.
Vậy đồ thị hàm số $y=\frac{2x+3}{x+1}$ có tiệm cận đứng là $x=-1$.
$\underset{x\to -{{1}^{+}}}{\mathop{\lim }}\,y=\underset{x\to -{{1}^{+}}}{\mathop{\lim }}\,\frac{2x+3}{x+1}=+\infty $ và $\underset{x\to -{{1}^{-}}}{\mathop{\lim }}\,y=\underset{x\to -{{1}^{-}}}{\mathop{\lim }}\,\frac{2x+3}{x+1}=-\infty $.
Vậy đồ thị hàm số $y=\frac{2x+3}{x+1}$ có tiệm cận đứng là $x=-1$.
\( x + y - z + 8 = 0 \). Vector nào sau đây là một vector pháp tuyến của mặt phẳng \( (P) \)?
A. \( \vec{n}_3 (1;1; - 1) \)
B. \( \vec{n}_1 (1;-1;1) \)
C. \( \vec{n}_4 (1;1;8) \)
D. \( \vec{n}_2 (1;-1;-1) \)
Ta có $\left( P \right)$: $x+y-z+8=0$ có véc tơ pháp tuyến $\overrightarrow{{{n}_{3}}}=\left( 1;\,1;\,-1 \right)$.
Vậy một véc tơ pháp tuyến của mặt phẳng $\left( P \right)$ là $\overrightarrow{{{n}_{3}}}=\left( 1;\,1;\,-1 \right)$.
Vậy một véc tơ pháp tuyến của mặt phẳng $\left( P \right)$ là $\overrightarrow{{{n}_{3}}}=\left( 1;\,1;\,-1 \right)$.

Gọi \( s_1, s_2 \) lần lượt là độ lệch chuẩn của mẫu số liệu ghép nhóm \( M_1, M_2 \). Phát biểu nào sau đây là đúng?
A. \( s_2 = 2s_1 \)
B. \( s_1 = s_2 \)
C. \( s_2 = \dfrac{3}{2}s_1 \)
D. \( s_1 = \dfrac{3}{2}s_2 \)
Ta có các bảng thống kê sau:
${{M}_{1}}$
${{M}_{2}}$
Số trung bình cộng của mẫu số liệu ghép nhóm ${{M}_{1}}$
${{\overline{x}}_{1}}=\frac{6\cdot 9+11\cdot 4+13\cdot 8+15\cdot 6+17.4}{28}=12,86$.
Phương sai của mẫu số liệu ghép nhóm ${{M}_{1}}$
$s_{1}^{2}=\frac{1}{28}\left[ 6.{{(9-12,86)}^{2}}+4\cdot {{(11-12,86)}^{2}}+8\cdot {{(13-12,86)}^{2}} \right.+6.{{(15-12,86)}^{2}}$
$+4.{{(17-12,86)}^{2}}]=7,12246$
Độ lệch chuẩn của mẫu số liệu ghép nhóm ${{M}_{1}}$là: ${{s}_{1}}=\sqrt{7,12246}\approx 2,67.$
Số trung bình cộng của mẫu số liệu ghép nhóm ${{M}_{2}}$
${{\overline{x}}_{_{2}}}=\frac{9\cdot 9+11\cdot 6+13\cdot 12+15\cdot 9+17.6}{42}=12,86$.
Phương sai của mẫu số liệu ghép nhóm ${{M}_{2}}$
$s_{2}^{2}=\frac{1}{42}\left[ 9.{{(9-12,86)}^{2}}+6.{{(11-12,86)}^{2}}+12.{{(13-12,86)}^{2}} \right.+9.{{(15-12,86)}^{2}}$
$+6.{{(17-12,86)}^{2}}]=7,12246.$
Độ lệch chuẩn của mẫu số liệu ghép nhóm ${{M}_{2}}$là: ${{s}_{2}}=\sqrt{7,12246}\approx 2,67.$
Vậy ${{s}_{1}}={{s}_{2}}$.
${{M}_{1}}$
| Nhóm | [8;10) | [10;12) | [12;14) | [14;16) | [16;18) |
| Giá trị đại diện | 9 | 11 | 13 | 15 | 17 |
| Tần số | 6 | 4 | 8 | 6 | 4 |
| Nhóm | [8;10) | [10;12) | [12;14) | [14;16) | [16;18) |
| Giá trị đại diện | 9 | 11 | 13 | 15 | 17 |
| Tần số | 9 | 6 | 12 | 9 | 6 |
${{\overline{x}}_{1}}=\frac{6\cdot 9+11\cdot 4+13\cdot 8+15\cdot 6+17.4}{28}=12,86$.
Phương sai của mẫu số liệu ghép nhóm ${{M}_{1}}$
$s_{1}^{2}=\frac{1}{28}\left[ 6.{{(9-12,86)}^{2}}+4\cdot {{(11-12,86)}^{2}}+8\cdot {{(13-12,86)}^{2}} \right.+6.{{(15-12,86)}^{2}}$
$+4.{{(17-12,86)}^{2}}]=7,12246$
Độ lệch chuẩn của mẫu số liệu ghép nhóm ${{M}_{1}}$là: ${{s}_{1}}=\sqrt{7,12246}\approx 2,67.$
Số trung bình cộng của mẫu số liệu ghép nhóm ${{M}_{2}}$
${{\overline{x}}_{_{2}}}=\frac{9\cdot 9+11\cdot 6+13\cdot 12+15\cdot 9+17.6}{42}=12,86$.
Phương sai của mẫu số liệu ghép nhóm ${{M}_{2}}$
$s_{2}^{2}=\frac{1}{42}\left[ 9.{{(9-12,86)}^{2}}+6.{{(11-12,86)}^{2}}+12.{{(13-12,86)}^{2}} \right.+9.{{(15-12,86)}^{2}}$
$+6.{{(17-12,86)}^{2}}]=7,12246.$
Độ lệch chuẩn của mẫu số liệu ghép nhóm ${{M}_{2}}$là: ${{s}_{2}}=\sqrt{7,12246}\approx 2,67.$
Vậy ${{s}_{1}}={{s}_{2}}$.
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4.
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.Câu 1. Cho hàm số \( f(x) = 2\sin x + x \).
a) \( f(0) = 0; \quad f(\pi) = \pi \).
b) Đạo hàm của hàm số đã cho là \( f'(x) = -2\cos x + 1 \).
c) Số nghiệm của phương trình \( f'(x) = 0 \) trên đoạn \([0; 3\pi]\) là 6.
d) Giá trị lớn nhất của \( f(x) \) trên đoạn \([0; \pi] \) là \( \dfrac{2\pi}{3} + \sqrt{3} \).
a) Đúng.
Ta có: $\left\{ \begin{align} & f\left( 0 \right)=2\sin 0+0=0 \\ & f\left( \pi \right)=2\sin \pi +\pi =\pi \\ \end{align} \right.$.
b) Sai.
Ta có: $y=f\left( x \right)=2\sin x+x$ suy ra ${f}'\left( x \right)=2\cos x+1$.
c) Sai.
Xét trên đoạn $\left[ 0;3\pi \right]$, ta có:
${f}'\left( x \right)=0$ $\Leftrightarrow $ $2\cos x+1=0$ $\Leftrightarrow $ $\cos x=\frac{-1}{2}$ $\Leftrightarrow $ $\left[ \begin{align} & x=\frac{2\pi }{3}+m2\pi \\ & x=-\frac{2\pi }{3}+n2\pi \\ \end{align} \right.$ $\left( m;n\in \mathbb{Z} \right)$.
Vì $0\le x\le 3\pi $ nên $\left[ \begin{align} & 0\le \frac{2\pi }{3}+m2\pi \le 3\pi \\ & 0\le -\frac{2\pi }{3}+n2\pi \le 3\pi \\ \end{align} \right.$ suy ra $\left[ \begin{align} & \frac{-1}{3}\le m\le \frac{7}{6} \\ & \frac{1}{3}\le n\le \frac{11}{6} \\ \end{align} \right.$.
Mà $m;n\in \mathbb{Z}$ nên $m\in \left\{ 0;1 \right\}$ và $n\in \left\{ 1 \right\}$
Vậy phương trình ${f}'\left( x \right)=0$ có ba nghiệm trên đoạn $\left[ 0;3\pi \right]$ .
d) Đúng.
Xét trên đoạn $\left[ 0;\pi \right]$, ta có:
${f}'\left( x \right)=0$ $\Leftrightarrow $ $2\cos x+1=0$ $\Leftrightarrow $ $\cos x=\frac{-1}{2}$ $\Leftrightarrow $ $x=\pm \frac{2\pi }{3}+k2\pi $ $\left( k\in \mathbb{Z} \right)$.
Vì $0\le x\le \frac{\pi }{2}$ nên $x=\frac{2\pi }{3}$.
Ta có: $\left\{ \begin{align} & f\left( 0 \right)=2\sin 0+0=0 \\ & f\left( \frac{2\pi }{3} \right)=2\sin \frac{2\pi }{3}+\frac{2\pi }{3}=\frac{2\pi }{3}+\sqrt{3} \\ & f\left( \pi \right)=2\sin \pi +\pi =\pi \\ \end{align} \right.$.
Vậy giá trị lớn nhất của $f\left( x \right)$ trên đoạn $\left[ 0;\pi \right]$ là $\frac{2\pi }{3}+\sqrt{3}$ khi $x=\frac{2\pi }{3}$.
Ta có: $\left\{ \begin{align} & f\left( 0 \right)=2\sin 0+0=0 \\ & f\left( \pi \right)=2\sin \pi +\pi =\pi \\ \end{align} \right.$.
b) Sai.
Ta có: $y=f\left( x \right)=2\sin x+x$ suy ra ${f}'\left( x \right)=2\cos x+1$.
c) Sai.
Xét trên đoạn $\left[ 0;3\pi \right]$, ta có:
${f}'\left( x \right)=0$ $\Leftrightarrow $ $2\cos x+1=0$ $\Leftrightarrow $ $\cos x=\frac{-1}{2}$ $\Leftrightarrow $ $\left[ \begin{align} & x=\frac{2\pi }{3}+m2\pi \\ & x=-\frac{2\pi }{3}+n2\pi \\ \end{align} \right.$ $\left( m;n\in \mathbb{Z} \right)$.
Vì $0\le x\le 3\pi $ nên $\left[ \begin{align} & 0\le \frac{2\pi }{3}+m2\pi \le 3\pi \\ & 0\le -\frac{2\pi }{3}+n2\pi \le 3\pi \\ \end{align} \right.$ suy ra $\left[ \begin{align} & \frac{-1}{3}\le m\le \frac{7}{6} \\ & \frac{1}{3}\le n\le \frac{11}{6} \\ \end{align} \right.$.
Mà $m;n\in \mathbb{Z}$ nên $m\in \left\{ 0;1 \right\}$ và $n\in \left\{ 1 \right\}$
Vậy phương trình ${f}'\left( x \right)=0$ có ba nghiệm trên đoạn $\left[ 0;3\pi \right]$ .
d) Đúng.
Xét trên đoạn $\left[ 0;\pi \right]$, ta có:
${f}'\left( x \right)=0$ $\Leftrightarrow $ $2\cos x+1=0$ $\Leftrightarrow $ $\cos x=\frac{-1}{2}$ $\Leftrightarrow $ $x=\pm \frac{2\pi }{3}+k2\pi $ $\left( k\in \mathbb{Z} \right)$.
Vì $0\le x\le \frac{\pi }{2}$ nên $x=\frac{2\pi }{3}$.
Ta có: $\left\{ \begin{align} & f\left( 0 \right)=2\sin 0+0=0 \\ & f\left( \frac{2\pi }{3} \right)=2\sin \frac{2\pi }{3}+\frac{2\pi }{3}=\frac{2\pi }{3}+\sqrt{3} \\ & f\left( \pi \right)=2\sin \pi +\pi =\pi \\ \end{align} \right.$.
Vậy giá trị lớn nhất của $f\left( x \right)$ trên đoạn $\left[ 0;\pi \right]$ là $\frac{2\pi }{3}+\sqrt{3}$ khi $x=\frac{2\pi }{3}$.
a) Một bóng đèn màu vàng là 0,6.
b) Một bóng đèn không hỏng, biết nó màu trắng là 0,97.
c) Một bóng đèn không hỏng, biết nó màu vàng là 0,98
d) Một bóng đèn không hỏng là 0,974.
Gọi biến cố $A:$ “Chọn được bóng đèn màu trắng”, biến cố $B:$ “Chọn được bóng đèn hỏng”.
Ta có: $P\left( A \right)=0,6$ suy ra $P\left( \overline{A} \right)=0,4$ và $P\left( B|A \right)=0,03$, $P\left( B|\overline{A} \right)=0,02$.
a) Sai.
Xác suất để bạn chọn được một bóng đèn màu vàng là $P\left( \overline{A} \right)=0,4$.
b) Đúng.
Xác suất để bạn chọn được một bóng đèn không hỏng, biết nó màu trắng là
$P\left( \overline{B}|A \right)=1-P\left( B|A \right)=0,97$.
c) Đúng.
Xác suất để bạn chọn được một bóng đèn không hỏng, biết nó màu vàng là
$P\left( \overline{B}|\overline{A} \right)=1-P\left( B|\overline{A} \right)=0,98$.
d) Đúng.
Xác suất để bạn chọn được một bóng đèn không hỏng là
$\begin{array}{l} P\left( {\overline B } \right) = P\left( {\overline B |A} \right).P\left( A \right) + P\left( {\overline B |\overline A } \right).P\left( {\overline A } \right)\\ = 0,97.0,6 + 0,98.0,4\\ = 0,974 \end{array}$
Ta có: $P\left( A \right)=0,6$ suy ra $P\left( \overline{A} \right)=0,4$ và $P\left( B|A \right)=0,03$, $P\left( B|\overline{A} \right)=0,02$.
a) Sai.
Xác suất để bạn chọn được một bóng đèn màu vàng là $P\left( \overline{A} \right)=0,4$.
b) Đúng.
Xác suất để bạn chọn được một bóng đèn không hỏng, biết nó màu trắng là
$P\left( \overline{B}|A \right)=1-P\left( B|A \right)=0,97$.
c) Đúng.
Xác suất để bạn chọn được một bóng đèn không hỏng, biết nó màu vàng là
$P\left( \overline{B}|\overline{A} \right)=1-P\left( B|\overline{A} \right)=0,98$.
d) Đúng.
Xác suất để bạn chọn được một bóng đèn không hỏng là
$\begin{array}{l} P\left( {\overline B } \right) = P\left( {\overline B |A} \right).P\left( A \right) + P\left( {\overline B |\overline A } \right).P\left( {\overline A } \right)\\ = 0,97.0,6 + 0,98.0,4\\ = 0,974 \end{array}$
a) Chiếc thứ nhất cách điểm xuất phát 87,57m.
b) Chiếc thứ hai cách điểm xuất phát 53,85m.
c) Khoảng cách giữa hai chiếc drone là 118,32m.
d) Trong các vị trí trên mặt đất quan sát hai drone có một vị trí mà tổng khoảng cách từ vị trí này đến hai drone nhỏ nhất và tổng này bằng 141,42m.
Gọi hệ trục toạ độ $Oxyz$ như hình vẽ. Xem mặt đất là mặt phẳng $Oxy$, vị trí ban đầu của hai drone là điểm $O$, gốc toạ độ.
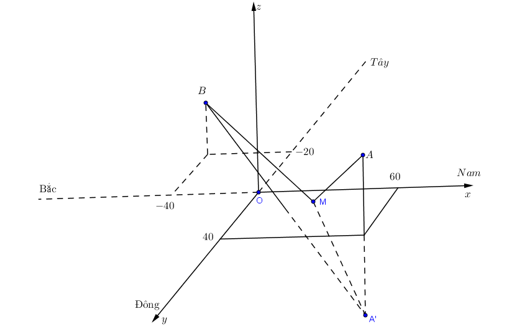
Gọi $A\left( 60,40,50 \right)$ là vị trí của drone thứ nhất sau khi xuất phát, $B\left( -40,-20,30 \right)$ là vị trí của drone thứ hai sau xuất phát.
a) Chiếc thứ nhất cách điểm xuất phát là $OA=\sqrt{{{60}^{2}}+{{40}^{2}}+{{50}^{2}}}\approx 87,75$
Chọn Sai
b) Chiếc thứ nhất cách điểm xuất phát là $OB=\sqrt{{{\left( -40 \right)}^{2}}+{{\left( -20 \right)}^{2}}+{{30}^{2}}}\approx 53,85$.
Chọn Đúng
c) Khoảng cách giữa hai chiếc drone là
$AB=\sqrt{{{\left( -40-60 \right)}^{2}}+{{\left( -20-40 \right)}^{2}}+{{\left( 30-50 \right)}^{2}}}\approx 118,32$.
Chọn Đúng
d) Gọi ${A}'$ là điểm đối xứng với $A$ qua mặt phẳng $Oxy$. Khi đó ${A}'\left( 60,40,-50 \right)$.
Gọi $M$ là vị trí trên mặt đất quan sát hai drone. Khi đó
$\begin{array}{l} MA + MB = MA' + MB \ge A'B = \sqrt {{{\left( { - 40 - 60} \right)}^2} + {{\left( { - 20 - 40} \right)}^2} + {{\left( {30 - \left( { - 50} \right)} \right)}^2}} \\ \approx 141,42 \end{array}$
Vậy tổng khoảng cách từ vị trí trên mặt đất đến hai drone nhỏ nhất là $141,42\,m$.
Chọn Đúng

Gọi $A\left( 60,40,50 \right)$ là vị trí của drone thứ nhất sau khi xuất phát, $B\left( -40,-20,30 \right)$ là vị trí của drone thứ hai sau xuất phát.
a) Chiếc thứ nhất cách điểm xuất phát là $OA=\sqrt{{{60}^{2}}+{{40}^{2}}+{{50}^{2}}}\approx 87,75$
Chọn Sai
b) Chiếc thứ nhất cách điểm xuất phát là $OB=\sqrt{{{\left( -40 \right)}^{2}}+{{\left( -20 \right)}^{2}}+{{30}^{2}}}\approx 53,85$.
Chọn Đúng
c) Khoảng cách giữa hai chiếc drone là
$AB=\sqrt{{{\left( -40-60 \right)}^{2}}+{{\left( -20-40 \right)}^{2}}+{{\left( 30-50 \right)}^{2}}}\approx 118,32$.
Chọn Đúng
d) Gọi ${A}'$ là điểm đối xứng với $A$ qua mặt phẳng $Oxy$. Khi đó ${A}'\left( 60,40,-50 \right)$.
Gọi $M$ là vị trí trên mặt đất quan sát hai drone. Khi đó
$\begin{array}{l} MA + MB = MA' + MB \ge A'B = \sqrt {{{\left( { - 40 - 60} \right)}^2} + {{\left( { - 20 - 40} \right)}^2} + {{\left( {30 - \left( { - 50} \right)} \right)}^2}} \\ \approx 141,42 \end{array}$
Vậy tổng khoảng cách từ vị trí trên mặt đất đến hai drone nhỏ nhất là $141,42\,m$.
Chọn Đúng

Giả sử hình tạo bởi các đoạn giao tuyến của \( (H) \) với mặt phẳng \( (\alpha) \) vuông góc với \( SO \) là một lục giác đều. Biết rằng khi mặt phẳng \( (\alpha) \) đi qua trung điểm của \( SO \) thì lục giác đều có cạnh \( l = 2(m) \).
a) Diện tích hình lục giác đều nói trên khi \( (\alpha) \) đi qua trung điểm của \( SO \) là \( 6\sqrt{3} \, (m^2) \).
b) Chọn hệ trục tọa độ \( Oxy \) sao cho gốc tọa độ là điểm \( O \) trên hình vẽ, \( S \) thuộc tia \( Oy \), đỉnh \( A \) của lục giác đều thuộc tia \( Ox \) thì \( c_4 \) nằm trên đường parabol có phương trình: $ y = \frac{1}{6}x^2 - \frac{17}{6}x + 10. $
c) Nếu \( (\alpha) \) cắt \( SO \) và \( c_4 \) lần lượt tại \( M \) và \( B \), mà \( OM = t \) thì độ dài đoạn \( BM \) là $ \frac{17}{2} - t + \sqrt{ \frac{49}{4} - t^2 }. $
d) Thể tích phần không gian nằm bên trong mái chòi \( (H) \) là \( 171{,}4 \, m^3 \).
a) Chia hình lục giác đều thành 6 tam giác đều. Khi đó diện tích hình lục giác đều khi $\left( \alpha \right)$ đi qua trung điểm của $SO$ là $6\cdot \frac{\sqrt{3}}{4}\cdot {{2}^{2}}=6\sqrt{3}\,\left( {{m}^{2}} \right)$.
Chọn Đúng
b) Gọi parabol chứa ${{c}_{4}}$ có phương trình là $y=a{{x}^{2}}+bx+c$.
Gọi $I$ là giao điểm của mặt phẳng $\left( \alpha \right)$ và ${{c}_{4}}$ khi mặt phẳng $\left( \alpha \right)$ đi qua trung điểm của $SO$ nên $I$ có toạ độ là $\left( 2,5 \right)$.
Do parabol đi qua ba điểm $S\left( 0,10 \right)$, $I\left( 2,5 \right)$, $A\left( 5,0 \right)$ nên phương trình của parabol là $y=\frac{1}{6}{{x}^{2}}-\frac{17}{6}x+10$.
Chọn Đúng
c) Khi $OM=t$ thì điểm $B$ có tung độ là $y=t$. Khi đó hoành độ của điểm $B$ là nghiệm nhỏ hơn của phương trình $\frac{1}{6}{{x}^{2}}-\frac{17}{6}x+10=t$ hay $\frac{1}{6}{{x}^{2}}-\frac{17}{6}x+10-t=0$.
Ta có $\Delta ={{\left( -\frac{17}{6} \right)}^{2}}-4\cdot \frac{1}{6}\cdot \left( 10-t \right)=\frac{49}{36}+\frac{2}{3}\cdot t$ nên hoành độ của điểm $B$ là ${{x}_{B}}=\frac{\frac{17}{6}-\sqrt{\frac{49}{36}+\frac{2}{3}\cdot t}}{\frac{1}{3}}=\frac{17}{2}-\sqrt{\frac{49}{4}+6t}$
Vậy độ dài đoạn $BM=\frac{17}{2}-\sqrt{\frac{49}{4}+6t}$.
Chọn Sai.
d) Diện tích hình phẳng giới hạn bởi mặt phẳng $\left( \alpha \right)$ và phần mái chòi là $S=6\cdot \frac{\sqrt{3}}{4}\cdot {{\left( \frac{17}{2}-\sqrt{\frac{49}{4}+6t} \right)}^{2}}$.
Khi đó thể tích của mái chòi là $V=\int\limits_{0}^{10}{6\cdot \frac{\sqrt{3}}{4}\cdot {{\left( \frac{17}{2}-\sqrt{\frac{49}{4}+6t} \right)}^{2}}dt=171,4\,\left( {{m}^{3}} \right)}$.
Chọn Đúng
Chọn Đúng
b) Gọi parabol chứa ${{c}_{4}}$ có phương trình là $y=a{{x}^{2}}+bx+c$.
Gọi $I$ là giao điểm của mặt phẳng $\left( \alpha \right)$ và ${{c}_{4}}$ khi mặt phẳng $\left( \alpha \right)$ đi qua trung điểm của $SO$ nên $I$ có toạ độ là $\left( 2,5 \right)$.
Do parabol đi qua ba điểm $S\left( 0,10 \right)$, $I\left( 2,5 \right)$, $A\left( 5,0 \right)$ nên phương trình của parabol là $y=\frac{1}{6}{{x}^{2}}-\frac{17}{6}x+10$.
Chọn Đúng
c) Khi $OM=t$ thì điểm $B$ có tung độ là $y=t$. Khi đó hoành độ của điểm $B$ là nghiệm nhỏ hơn của phương trình $\frac{1}{6}{{x}^{2}}-\frac{17}{6}x+10=t$ hay $\frac{1}{6}{{x}^{2}}-\frac{17}{6}x+10-t=0$.
Ta có $\Delta ={{\left( -\frac{17}{6} \right)}^{2}}-4\cdot \frac{1}{6}\cdot \left( 10-t \right)=\frac{49}{36}+\frac{2}{3}\cdot t$ nên hoành độ của điểm $B$ là ${{x}_{B}}=\frac{\frac{17}{6}-\sqrt{\frac{49}{36}+\frac{2}{3}\cdot t}}{\frac{1}{3}}=\frac{17}{2}-\sqrt{\frac{49}{4}+6t}$
Vậy độ dài đoạn $BM=\frac{17}{2}-\sqrt{\frac{49}{4}+6t}$.
Chọn Sai.
d) Diện tích hình phẳng giới hạn bởi mặt phẳng $\left( \alpha \right)$ và phần mái chòi là $S=6\cdot \frac{\sqrt{3}}{4}\cdot {{\left( \frac{17}{2}-\sqrt{\frac{49}{4}+6t} \right)}^{2}}$.
Khi đó thể tích của mái chòi là $V=\int\limits_{0}^{10}{6\cdot \frac{\sqrt{3}}{4}\cdot {{\left( \frac{17}{2}-\sqrt{\frac{49}{4}+6t} \right)}^{2}}dt=171,4\,\left( {{m}^{3}} \right)}$.
Chọn Đúng
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
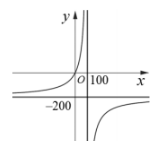
Câu 1. Để loại bỏ \( x\% \) chất gây ô nhiễm môi trường từ khí thải của một nhà máy, người ta ước tính chi phí (triệu đồng) cần bỏ ra được mô hình hóa bởi hàm số có dạng $C(x) = \frac{ax + b}{-x + d} \quad \text{(hữu tỉ, với } 0 \leq x < 100).$ Tính chi phí chênh lệch (tỉ đồng) phải bỏ ra để loại bỏ 90% và loại bỏ 99% chất gây ô nhiễm từ khí thải của nhà máy.
:
Đáp số: 18
Dựa vào đồ thị hàm số ta thấy đồ thị hàm số $C\left( x \right)=\frac{ax+b}{-x+d}$ có:
+) tiệm cận đứng là $x=100$$\Rightarrow C\left( x \right)=\frac{ax+b}{-x+100}$..
+) tiệm cận ngang là $y=-200$$\Rightarrow C\left( x \right)=\frac{200x+b}{-x+100}$..
+) đi qua gốc tọa độ $O\left( 0;0 \right)$$\Rightarrow C\left( x \right)=\frac{200x}{-x+100}$.
Ta có $C\left( 90 \right)=1800$(triệu đồng)
$C\left( 99 \right)=19800$(triệu đồng)
Chi phí chênh lệch là $C\left( 99 \right)-C\left( 90 \right)=18000$ (triệu đồng) =18 (tỉ đồng)
Đáp số: 18
Dựa vào đồ thị hàm số ta thấy đồ thị hàm số $C\left( x \right)=\frac{ax+b}{-x+d}$ có:
+) tiệm cận đứng là $x=100$$\Rightarrow C\left( x \right)=\frac{ax+b}{-x+100}$..
+) tiệm cận ngang là $y=-200$$\Rightarrow C\left( x \right)=\frac{200x+b}{-x+100}$..
+) đi qua gốc tọa độ $O\left( 0;0 \right)$$\Rightarrow C\left( x \right)=\frac{200x}{-x+100}$.
Ta có $C\left( 90 \right)=1800$(triệu đồng)
$C\left( 99 \right)=19800$(triệu đồng)
Chi phí chênh lệch là $C\left( 99 \right)-C\left( 90 \right)=18000$ (triệu đồng) =18 (tỉ đồng)

:
Đáp số: 8
Đặt $HE=x\left( 0\le x\le 20 \right)$$\Rightarrow $$KF=20-x$
$\Rightarrow $$AE=\sqrt{16+{{x}^{2}}}$, $KB=\sqrt{36+{{\left( 20-x \right)}^{2}}}$
Đường đi từ thành phố $A$đến thành phố $B$(đi theo đường $AEFB$) là $AE+EF+KB$.
Để đường đi từ thành phố $A$đến thành phố $B$là ngắn nhất thì $AE+KB$ đạt giá trị nhỏ nhất (vì $EF$ không đổi).
Đặt $f\left( x \right)=AE+KB=\sqrt{16+{{x}^{2}}}+\sqrt{36+{{\left( 20-x \right)}^{2}}}$.
$f'\left( x \right)=\frac{x}{\sqrt{16+{{x}^{2}}}}-\frac{20-x}{\sqrt{36+{{\left( 20-x \right)}^{2}}}}$
$f'\left( x \right)=0\Leftrightarrow \frac{x}{\sqrt{16+{{x}^{2}}}}-\frac{20-x}{\sqrt{36+{{\left( 20-x \right)}^{2}}}}=0$
$\Leftrightarrow \frac{x}{\sqrt{16+{{x}^{2}}}}=\frac{20-x}{\sqrt{36+{{\left( 20-x \right)}^{2}}}}$$\Leftrightarrow \left[ \begin{align} & x=8\left( N \right) \\ & x=-40\left( L \right) \\ \end{align} \right.$.
Bảng biến thiên
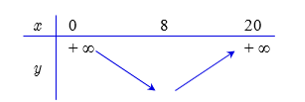
Vậy độ dài $EH=8$$km$thì đường đi từ thành phố $A$ đến thành phố $B$ là ngắn nhất.
Đáp số: 8
Đặt $HE=x\left( 0\le x\le 20 \right)$$\Rightarrow $$KF=20-x$
$\Rightarrow $$AE=\sqrt{16+{{x}^{2}}}$, $KB=\sqrt{36+{{\left( 20-x \right)}^{2}}}$
Đường đi từ thành phố $A$đến thành phố $B$(đi theo đường $AEFB$) là $AE+EF+KB$.
Để đường đi từ thành phố $A$đến thành phố $B$là ngắn nhất thì $AE+KB$ đạt giá trị nhỏ nhất (vì $EF$ không đổi).
Đặt $f\left( x \right)=AE+KB=\sqrt{16+{{x}^{2}}}+\sqrt{36+{{\left( 20-x \right)}^{2}}}$.
$f'\left( x \right)=\frac{x}{\sqrt{16+{{x}^{2}}}}-\frac{20-x}{\sqrt{36+{{\left( 20-x \right)}^{2}}}}$
$f'\left( x \right)=0\Leftrightarrow \frac{x}{\sqrt{16+{{x}^{2}}}}-\frac{20-x}{\sqrt{36+{{\left( 20-x \right)}^{2}}}}=0$
$\Leftrightarrow \frac{x}{\sqrt{16+{{x}^{2}}}}=\frac{20-x}{\sqrt{36+{{\left( 20-x \right)}^{2}}}}$$\Leftrightarrow \left[ \begin{align} & x=8\left( N \right) \\ & x=-40\left( L \right) \\ \end{align} \right.$.
Bảng biến thiên

Vậy độ dài $EH=8$$km$thì đường đi từ thành phố $A$ đến thành phố $B$ là ngắn nhất.
Đáp án: 216
Giả sử tập con bất kì $\left\{ a,b,c \right\}\in S,1\le a,b,c\le 100,\,a,b,c$ phân biệt.
Ta có $a+b+c=91$. Số bộ $a,b,c$ là $C_{91-1}^{3-1}=C_{90}^{2}$ (bài toán chia kẹo).
Tuy nhiên trong các bộ trên vẫn chứa các bộ có 2 số giống nhau như $\left\{ 1;1;89 \right\},...,\left\{ 45;45;1 \right\}$, mỗi bộ lại có 3 bộ tương ứng. Số bộ có 2 số giống nhau là $3.45=135$.
Số phần tử của không gian mẫu là $n\left( \Omega \right)=\frac{C_{90}^{2}-135}{3!}=645$.
Giả sử ta chọn được 3 số $a,\,aq,\,a{{q}^{2}}$ với $q>0$.
Theo giả thiết ta có $a+aq+a{{q}^{2}}=91\Leftrightarrow a.\left( 1+q+{{q}^{2}} \right)=91$.
Do $91=7.13=1.91$ và $a$ , $q$ đều là các số nguyên dương nên ta có các trường hợp sau:
+ Trường hợp 1:$\left\{ \begin{array}{l} a = 7\\ 1 + q + {q^2} = 13 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = 7\\ \left[ \begin{array}{l} q = 3\,\left( {tm} \right)\\ q = - 4\,\left( {ktm} \right) \end{array} \right. \end{array} \right.$.
Ta có bộ số thỏa mãn $\left\{ 7;21;63 \right\}$.
+ Trường hợp 2: $\left\{ \begin{array}{l} a = 13\\ 1 + q + {q^2} = 7 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = 7\\ \left[ \begin{array}{l} q = 2\,\left( {tm} \right)\\ q = - 3\,\left( {ktm} \right) \end{array} \right. \end{array} \right.$. Ta có bộ số thỏa mãn $\left\{ 13;26;52 \right\}$.
+ Trường hợp 3: $\left\{ \begin{array}{l} a = 1\\ 1 + q + {q^2} = 91 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = 1\\ \left[ \begin{array}{l} q = 9\,\left( {tm} \right)\\ q = - 10\,\left( {ktm} \right) \end{array} \right. \end{array} \right.$. Ta có bộ số thỏa mãn $\left\{ 1;9;81 \right\}$.
+ Trường hợp 4: $\left\{ \begin{array}{l} a = 91\\ 1 + q + {q^2} = 1 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = 91\\ \left[ \begin{array}{l} q = 0\,\left( {ktm} \right)\\ q = - 1\,\left( {ktm} \right) \end{array} \right. \end{array} \right.$.
Xác suất cần tìm là $p=\frac{3}{645}=\frac{1}{215}$$\Rightarrow m=1;\,n=215$. Vậy $m+n=216$.
Giả sử tập con bất kì $\left\{ a,b,c \right\}\in S,1\le a,b,c\le 100,\,a,b,c$ phân biệt.
Ta có $a+b+c=91$. Số bộ $a,b,c$ là $C_{91-1}^{3-1}=C_{90}^{2}$ (bài toán chia kẹo).
Tuy nhiên trong các bộ trên vẫn chứa các bộ có 2 số giống nhau như $\left\{ 1;1;89 \right\},...,\left\{ 45;45;1 \right\}$, mỗi bộ lại có 3 bộ tương ứng. Số bộ có 2 số giống nhau là $3.45=135$.
Số phần tử của không gian mẫu là $n\left( \Omega \right)=\frac{C_{90}^{2}-135}{3!}=645$.
Giả sử ta chọn được 3 số $a,\,aq,\,a{{q}^{2}}$ với $q>0$.
Theo giả thiết ta có $a+aq+a{{q}^{2}}=91\Leftrightarrow a.\left( 1+q+{{q}^{2}} \right)=91$.
Do $91=7.13=1.91$ và $a$ , $q$ đều là các số nguyên dương nên ta có các trường hợp sau:
+ Trường hợp 1:$\left\{ \begin{array}{l} a = 7\\ 1 + q + {q^2} = 13 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = 7\\ \left[ \begin{array}{l} q = 3\,\left( {tm} \right)\\ q = - 4\,\left( {ktm} \right) \end{array} \right. \end{array} \right.$.
Ta có bộ số thỏa mãn $\left\{ 7;21;63 \right\}$.
+ Trường hợp 2: $\left\{ \begin{array}{l} a = 13\\ 1 + q + {q^2} = 7 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = 7\\ \left[ \begin{array}{l} q = 2\,\left( {tm} \right)\\ q = - 3\,\left( {ktm} \right) \end{array} \right. \end{array} \right.$. Ta có bộ số thỏa mãn $\left\{ 13;26;52 \right\}$.
+ Trường hợp 3: $\left\{ \begin{array}{l} a = 1\\ 1 + q + {q^2} = 91 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = 1\\ \left[ \begin{array}{l} q = 9\,\left( {tm} \right)\\ q = - 10\,\left( {ktm} \right) \end{array} \right. \end{array} \right.$. Ta có bộ số thỏa mãn $\left\{ 1;9;81 \right\}$.
+ Trường hợp 4: $\left\{ \begin{array}{l} a = 91\\ 1 + q + {q^2} = 1 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = 91\\ \left[ \begin{array}{l} q = 0\,\left( {ktm} \right)\\ q = - 1\,\left( {ktm} \right) \end{array} \right. \end{array} \right.$.
Xác suất cần tìm là $p=\frac{3}{645}=\frac{1}{215}$$\Rightarrow m=1;\,n=215$. Vậy $m+n=216$.

Lưu ý: Khoảng cách giữa thanh ngang và mặt sàn là độ dài đoạn thẳng nối một điểm thuộc thanh ngang đến hình chiếu của điểm đó trên mặt sàn.
Đáp án: 18,7
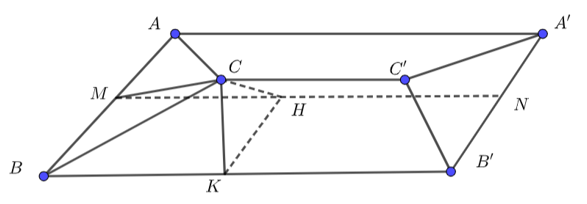
Gọi $M,N$ lần lượt là trung điểm của $AB,\,{A}'{B}'$.
Gọi $H,K$ lần lượt là hình chiếu vuông góc của $C$ lên $MN,\,B{B}'$.
Ta có $CH=2m;\,HK=3m\Rightarrow CK=\sqrt{C{{H}^{2}}+H{{K}^{2}}}=\sqrt{{{2}^{2}}+{{3}^{2}}}=\sqrt{13}m$.
Xét tam giác $CHM$ vuông tại $H$, có
$\begin{array}{l} MH = \frac{{10 - 6}}{2} = 2\\ \Rightarrow CM = \sqrt {C{H^2} + H{M^2}} \\ = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 m \end{array}$.
Tổng diện tích $S$ mái tôn bằng
$\begin{array}{l} S = {S_{\Delta ABC}} + {S_{\Delta A'B'C'}} + {S_{ACC'A'}} + {S_{BCC'B'}}\\ = 2.{S_{\Delta ABC}} + 2{S_{BCC'B'}}\\ = 2.\frac{1}{2}.CM.AB + 2.\frac{{\left( {BB' + CC'} \right).CK}}{2} \end{array}$
$=2.\frac{1}{2}.2\sqrt{2}.6+2.\frac{\left( 10+6 \right).\sqrt{13}}{2}=12\sqrt{2}+16\sqrt{13}\,{{m}^{2}}$.
Vậy số tiền bác An phải trả là $T=\left( 12\sqrt{2}+16\sqrt{13} \right)\,.250000=18664845,79\approx 18,7$(triệu đồng)

Gọi $M,N$ lần lượt là trung điểm của $AB,\,{A}'{B}'$.
Gọi $H,K$ lần lượt là hình chiếu vuông góc của $C$ lên $MN,\,B{B}'$.
Ta có $CH=2m;\,HK=3m\Rightarrow CK=\sqrt{C{{H}^{2}}+H{{K}^{2}}}=\sqrt{{{2}^{2}}+{{3}^{2}}}=\sqrt{13}m$.
Xét tam giác $CHM$ vuông tại $H$, có
$\begin{array}{l} MH = \frac{{10 - 6}}{2} = 2\\ \Rightarrow CM = \sqrt {C{H^2} + H{M^2}} \\ = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 m \end{array}$.
Tổng diện tích $S$ mái tôn bằng
$\begin{array}{l} S = {S_{\Delta ABC}} + {S_{\Delta A'B'C'}} + {S_{ACC'A'}} + {S_{BCC'B'}}\\ = 2.{S_{\Delta ABC}} + 2{S_{BCC'B'}}\\ = 2.\frac{1}{2}.CM.AB + 2.\frac{{\left( {BB' + CC'} \right).CK}}{2} \end{array}$
$=2.\frac{1}{2}.2\sqrt{2}.6+2.\frac{\left( 10+6 \right).\sqrt{13}}{2}=12\sqrt{2}+16\sqrt{13}\,{{m}^{2}}$.
Vậy số tiền bác An phải trả là $T=\left( 12\sqrt{2}+16\sqrt{13} \right)\,.250000=18664845,79\approx 18,7$(triệu đồng)

Biết diện tích mặt kính là \( a\sqrt{b} \, (dm^2) \), (với \( a \) là số nguyên dương và \( b \) là số nguyên tố). Tính \( a + b \).
Chọn hệ tọa độ $Oxy$ như hình vẽ
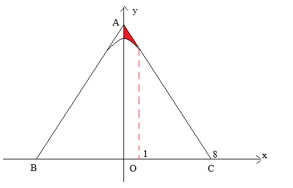
Tam giác $ABC$ đều cạnh bằng 16 nên $AO=8\sqrt{3}$, diện tích ${{S}_{\Delta ABC}}={{16}^{2}}.\frac{\sqrt{3}}{4}=64\sqrt{3}.$
Tọa độ các điểm $A\left( 0;8\sqrt{3} \right),C\left( 8;0 \right)$, do đó phương trình $AC:y=-\sqrt{3}x+8\sqrt{3}$.
Xác định hoành độ giao điểm của $\left( P \right)$ và $AC$. Xét phương trình
$\begin{array}{l} - \frac{{\sqrt 3 }}{2}{x^2} + \frac{{15\sqrt 3 }}{2} = - \sqrt 3 x + 8\sqrt 3 \\ \Leftrightarrow - \frac{{\sqrt 3 }}{2}{x^2} + \sqrt 3 x - \frac{{\sqrt 3 }}{2} \Rightarrow x = 1 \end{array}$
Diện tích phần tô màu trong hình là
$\begin{array}{l} {S_1} = \int\limits_0^1 {\left[ {\left( { - \sqrt 3 x + 8\sqrt 3 } \right) - \left( { - \frac{{\sqrt 3 }}{2}{x^2} + \frac{{15\sqrt 3 }}{2}} \right)} \right]{\rm{d}}} x\\ = \int\limits_0^1 {\left( {\frac{{\sqrt 3 }}{2}{x^2} - \sqrt 3 x + \frac{{\sqrt 3 }}{2}} \right){\rm{d}}x} \\ = \frac{{\sqrt 3 }}{2}\int\limits_0^1 {{{\left( {x - 1} \right)}^2}{\rm{d}}x} \\ = \left. {\frac{{\sqrt 3 }}{6}{{\left( {x - 1} \right)}^3}} \right|_0^1 = \frac{{\sqrt 3 }}{6}. \end{array}$
Diện tích tấm kính mặt bàn là $S={{S}_{\Delta ABC}}-6{{S}_{1}}=64\sqrt{3}-6\frac{\sqrt{3}}{6}=63\sqrt{3}$. Vậy $a+b=66$.

Tam giác $ABC$ đều cạnh bằng 16 nên $AO=8\sqrt{3}$, diện tích ${{S}_{\Delta ABC}}={{16}^{2}}.\frac{\sqrt{3}}{4}=64\sqrt{3}.$
Tọa độ các điểm $A\left( 0;8\sqrt{3} \right),C\left( 8;0 \right)$, do đó phương trình $AC:y=-\sqrt{3}x+8\sqrt{3}$.
Xác định hoành độ giao điểm của $\left( P \right)$ và $AC$. Xét phương trình
$\begin{array}{l} - \frac{{\sqrt 3 }}{2}{x^2} + \frac{{15\sqrt 3 }}{2} = - \sqrt 3 x + 8\sqrt 3 \\ \Leftrightarrow - \frac{{\sqrt 3 }}{2}{x^2} + \sqrt 3 x - \frac{{\sqrt 3 }}{2} \Rightarrow x = 1 \end{array}$
Diện tích phần tô màu trong hình là
$\begin{array}{l} {S_1} = \int\limits_0^1 {\left[ {\left( { - \sqrt 3 x + 8\sqrt 3 } \right) - \left( { - \frac{{\sqrt 3 }}{2}{x^2} + \frac{{15\sqrt 3 }}{2}} \right)} \right]{\rm{d}}} x\\ = \int\limits_0^1 {\left( {\frac{{\sqrt 3 }}{2}{x^2} - \sqrt 3 x + \frac{{\sqrt 3 }}{2}} \right){\rm{d}}x} \\ = \frac{{\sqrt 3 }}{2}\int\limits_0^1 {{{\left( {x - 1} \right)}^2}{\rm{d}}x} \\ = \left. {\frac{{\sqrt 3 }}{6}{{\left( {x - 1} \right)}^3}} \right|_0^1 = \frac{{\sqrt 3 }}{6}. \end{array}$
Diện tích tấm kính mặt bàn là $S={{S}_{\Delta ABC}}-6{{S}_{1}}=64\sqrt{3}-6\frac{\sqrt{3}}{6}=63\sqrt{3}$. Vậy $a+b=66$.

Gọi $O$ là trọng tâm của tam giác $ABC$, $M$ là trung điểm của $BC$.
Gọi $H,K$ lần lượt là hình chiếu vuông góc của $M,O$ lên $A{A}'$.
Tam giác $ABC$ đều cạnh bằng $2$ nên ${{S}_{\Delta ABC}}={{2}^{2}}.\frac{\sqrt{3}}{4}=\sqrt{3};\,\,AM=2.\frac{\sqrt{3}}{2}=\sqrt{3}$.
$AO=\frac{2}{3}AM=\frac{2\sqrt{3}}{3}$.
Ta có $MH$là đường vuông góc chung của $A{A}'$và $BC$ nên $MH=\frac{\sqrt{3}}{2}$.
$\frac{OK}{MH}=\frac{AO}{AM}=\frac{2}{3}\Rightarrow OK=\frac{2}{3}MH=\frac{2}{3}.\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3}$.
Tam giác $A{A}'O$ vuông tại $O$, nên
$\begin{array}{l} \frac{1}{{O{K^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{S^2}}}\\ \Rightarrow \frac{1}{{O{S^2}}} = \frac{1}{{O{K^2}}} - \frac{1}{{O{A^2}}}\\ = \frac{1}{{{{\left( {\frac{{\sqrt 3 }}{3}} \right)}^2}}} - \frac{1}{{{{\left( {\frac{{2\sqrt 3 }}{3}} \right)}^2}}} = \frac{9}{4}\\ \Rightarrow SO = \frac{2}{3} \end{array}$
Vậy thể tích khối lăng trụ $ABC.{A}'{B}'{C}'$ là ${{V}_{ABC.{A}'{B}'{C}'}}={{S}_{\Delta ABC}}.SO=\frac{2}{\sqrt{3}}\simeq 1,15\,\,\left( d{{m}^{3}} \right)$
