Đề khảo sát chất lượng môn Toán lớp 12 đợt 2 năm học 2024 – 2025 của Sở Giáo dục và Đào tạo Nghệ An. Bám sát cấu trúc đề thi tốt nghiệp THPT, có lời giải chi tiết giúp học sinh ôn luyện hiệu quả.
Câu 1. Trong không gian Oxyz, phương trình của đường thẳng đi qua A(-1,-1,1) và có vectơ chỉ phương $\vec{u}(1,2,3)$ là
A. $\frac{x-1}{-1} = \frac{y-2}{-1} = \frac{z-3}{1}$.
B. $\frac{x+1}{-1} = \frac{y+2}{-1} = \frac{z+3}{1}$.
C. $\frac{x+1}{1} = \frac{y+1}{2} = \frac{z-1}{3}$.
D. $\frac{x-1}{1} = \frac{y-1}{2} = \frac{z+1}{3}$.
Câu 2. Hai mẫu số liệu ghép nhóm $M_1$, $M_2$ có bảng tần số ghép nhóm như sau:
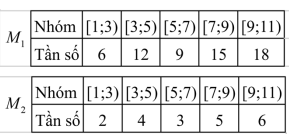
Gọi $s_1^2$, $s_2^2$ lần lượt là phương sai của mẫu số liệu ghép nhóm $M_1$, $M_2$. Phát biểu nào sau đây là đúng?
A. $s_1^2 = 3s_2^2$.
B. $3s_1^2 = s_2^2$.
C. $s_1^2 = 9s_2^2$.
D. $s_1^2 = s_2^2$.
Câu 3. Cho $\int_0^2 f(x)dx = 1$ và $\int_2^5 f(x)dx = 3$. Tính $\int_0^5 f(x)dx$.
A. $\int_0^5 f(x)dx = -2$.
B. $\int_0^5 f(x)dx = -3$.
C. $\int_0^5 f(x)dx = 2$.
D. $\int_0^5 f(x)dx = 4$.
Câu 4. Với $a$ là số thực dương thì $\log_a(3a)$ bằng
A. $a$.
B. $1-\log_a a$.
C. $1+\log_a a$.
D. $1+a$.
Câu 5. Cho cấp số nhân $(u_n)$ có $u_1 = 1$ và công bội $q = 2$. Tổng năm số hạng đầu tiên của cấp số nhân là
A. 16.
B. 25.
C. 31.
D. 32.
Câu 6. Hàm số nào sau đây có đồ thị như hình vẽ?

A. $y = \frac{x-2}{x+1}$.
B. $y = \frac{x^2+2x+2}{x+1}$.
C. $y = x^2-2x+3$.
D. $y = x^2-3x+2$.
Câu 7. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình $(x-1)^2+(y+2)^2+(z-3)^2 = 4$. Tâm I của mặt cầu (S) có tọa độ là
A. $I(-1;2;3)$.
B. $I(-1;2;-3)$.
C. $I(1;-2;-3)$.
D. $I(1;-2;3)$.
Câu 8. Cho hình hộp chữ nhật $ABCD.A'B'C'D'$.
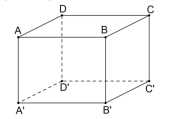
Mệnh đề nào sau đây đúng?
A. $\overrightarrow{AB}.\overrightarrow{AA'}= 0$.
B. $\overrightarrow{AB}.\overrightarrow{AC'}= 0$.
C. $\overrightarrow{AB}.\overrightarrow{BA'}= 0$.
D. $\overrightarrow{AB}.\overrightarrow{AC}= 0$.
Câu 9. Tập xác định của hàm số $y = \log_{\frac{1}{2}} x$ là
A. $(0; +\infty)$.
B. $(-\infty; 0)$.
C. $(-\infty; +\infty)$.
D. $[0; +\infty)$.
Câu 10. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ:
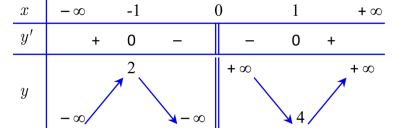
Hàm số nghịch biến trên khoảng nào dưới đây?
A. $(-\infty; -1)$.
B. $(4; +\infty)$.
C. $(-1;1)$.
D. $(0;1)$.
Câu 11. Cho hai biến cố $A$ và $B$ độc lập với nhau. Biết $P(A) = 0{,}4$ và $P(B) = 0{,}5$. Tính $P(AB)$.
A. 0,1.
B. 0,8.
C. 0,2.
D. 0,9.
Câu 12. Mệnh đề nào sau đây đúng?
A. $\left( \int \sin x \, dx \right)' = \sin x$.
B. $\left( \int \sin x \, dx \right)' = -\cos x + c$.
C. $\left( \int \sin x \, dx \right)' = \cos x$.
D. $\left( \int \sin x \, dx \right)' = -\cos x$.
Câu 1. Một doanh nghiệp sản xuất thực phẩm – đồ uống có tiền lương hàng tháng của các nhân viên được thống kê bởi bảng sau:
Gọi $Q_1, Q_3$ lần lượt là các tứ phân vị thứ nhất và tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên.
a) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là $\Delta_Q = Q_3 - Q_1$.
b) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên là $Q_3 = 20{,}833$.
c) Có ít nhất 75% nhân viên của doanh nghiệp có mức lương hàng tháng không vượt quá 17 triệu đồng.
d) Nếu một nhân viên của doanh nghiệp có mức lương là 34 triệu đồng / tháng thì lương của nhân viên này là một giá trị ngoại lệ.
Câu 2. Một trang trại cần xây một bể chứa nước hình trụ bằng bê tông (có nắp đậy) để chứa $60m^3$ nước tưới tiêu. Chi phí xây dựng chủ yếu phụ thuộc vào diện tích bề mặt bê tông cần sử dụng (diện tích toàn phần của bể tính theo phần bên trong của bể). Theo hợp đồng với nhà thầu xây dựng, chi phí mỗi mét vuông xây dựng theo cách tính trên là 1,5 triệu đồng. Gọi $r$ là bán kính đáy và $h$ là chiều cao của bể (đơn vị tính của $r, h$ là mét).
a) Thể tích của bể là: $V = \pi r^2 h = 60m^3$.
b) Diện tích toàn phần $S_p$ của bể chứa nước được biểu diễn theo bán kính $r$ là $S_p(r) = \pi r^2 + \frac{120}{r}$ (m²).
c) Để tiết kiệm chi phí nhất, bể nên được xây với bán kính đáy là $r = \sqrt{\frac{30}{\pi}}$ m.
d) Chi phí thấp nhất để xây dựng bể chứa nước nói trên là 127 triệu đồng (làm tròn kết quả đến hàng đơn vị).
Câu 3. Cho hàm số $f(x) = x^3 - 3x^2 + 2$ có đồ thị là đường cong $(C)$. Đường thẳng $d$ đi qua tâm đối xứng của $(C)$ và cắt $(C)$ tại hai điểm $A$ và $B$ (như hình vẽ). Biết điểm $A$ có hoành độ bằng -1.

a) Tọa độ tâm đối xứng của đồ thị hàm số $f(x)$ là $I(0;1)$.
b) Điểm $A$ có tung độ bằng $-2$.
c) Đường thẳng $d$ có phương trình là $y = x + 1$.
d) Diện tích hình phẳng giới hạn bởi đường cong $(C)$ và đường thẳng $d$ (phần gạch chéo) bằng 8.
Câu 4. Tại một nút giao thông của một khu vực đông dân cư với tốc độ tối đa cho phép đối với ô tô là 50 km/h, người ta gắn một camera phát nguội tại điểm $S(0; 0; 14)$ trong không gian $Oxyz$ (đơn vị trên mỗi trục tọa độ là mét), mặt phẳng $Oxy$ song song với mặt đường và chứa vùng nhận diện biển số xe của các phương tiện tham gia giao thông.
Biết rằng camera nhận diện tốt nhất biển số xe của các phương tiện tham gia giao thông là khi biển số của xe nằm trong hình thang cân $ABCD$ với: $SA = SB = 27$ m, $OD = OC = 5$ m, $AB = 14$ m, $CD = 9,6$ m và $AB \parallel CD$ nằm trên đường trung trực các đoạn thẳng $AB$ và $DC$ (xem hình vẽ minh họa).
Giả sử tại thời điểm 9h00' (được xem là thời điểm xuất phát) một ô tô chuyển động thẳng đều theo phương song song với trục $Ox$, hướng về phía trục $Oy$ và có vị trí của biển số xe là $M(50; -6; 0)$.
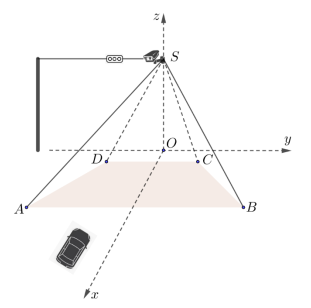
a) Điểm $D$ có tọa độ là $(1,4;\ -4,8;\ 0)$.
b) Đường thẳng $AD$ có phương trình là $ \begin{cases} x = 1,4 - 20,6t \\ y = -4,8 + 2,2t \ (t \in \mathbb{R}) \\ z = 0 \end{cases} $
c) Nếu ô tô đi với vận tốc 45 km/h thì sau đúng 2,2 giây kể từ thời điểm xuất phát thì biển số của xe ôtô đã nằm trong vùng nhận diện tốt nhất của camera.
d) Nếu camera ghi nhận được hình ảnh biển số xe ô tô liên tục trong một khoảng thời gian kéo dài đúng 0,7 giây, và khoảng thời gian 0,7 giây này kết thúc đồng thời với thời điểm xe vừa ra khỏi vùng nhận diện tốt nhất, thì ôtô đã vượt quá tốc độ cho phép.
Câu 1. Trong một cuộc diễn tập phòng không, một bệ phóng tên lửa phòng không được đặt tại vị trí $O\left(0; 0; 0\right)$ (trong không gian $Oxyz$ với đơn vị trên các hệ trục tính theo ki-lô-mét) có tầm bắn tối đa là 30 km và tên lửa được phóng ra với vận tốc không đổi là 500 m/s. Một máy bay không người lái bay theo một đường thẳng có vectơ chỉ phương $\vec{u} = (3; -4; 0)$ với vận tốc không đổi là 900 km/h. Khi phát hiện máy bay không người lái tại vị trí $A(6; -20; 16)$ thì tên lửa rời bệ phóng, khai hỏa và đã bắn hạ được mục tiêu. Hỏi khoảng cách từ bệ phóng tên lửa đến vị trí máy bay không người lái bị bắn hạ bằng bao nhiêu ki-lô-mét? (Giả sử cả máy bay không người lái và tên lửa đều bay theo đường thẳng và không chịu tác động của trọng lực hay lực cản không khí).
Câu 2. Một công ty thuê thợ vẽ logo công ty như hình vẽ lên một bức tường lớn. Logo có dạng là 1 bông hoa có 6 cánh hoa giống nhau, sắp xếp cách đều nhau như hình vẽ.

Để chính xác hóa kích thước và hình dạng khi vẽ, mỗi cánh hoa được thiết kế như sau: Trong mặt phẳng $Oxy$ (một đơn vị ứng với 1 mét trên thực tế), một cánh hoa được xem là một hình phẳng giới hạn bởi đồ thị hàm số bậc ba $y = \dfrac{(x - 3)^3}{27} + 1$ $(C)$ và một đường parabol $(P): y = ax^2 + bx + c \, (a \ne 0)$. $(C)$ và $(P)$ cắt nhau tại hai điểm $O(0;0), M(6;2)$ và $(P)$ đi qua điểm $N(3;0)$. Biết rằng chi phí vẽ logo nói trên được tính dựa trên mỗi mét vuông cánh hoa được vẽ, mỗi mét vuông được báo giá là 210 nghìn đồng. Hãy tính chi phí vẽ logo đó (đơn vị tính: nghìn đồng, làm tròn kết quả đến hàng đơn vị).
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB=2, AD=4 và SA⊥(ABCD). SA=2√5. Tính số đo góc giữa đường thẳng SC và mặt phẳng (SBD) (đơn vị đo góc: độ, làm tròn kết quả với hàng phần mười).
Câu 4. Hiệu quả nhiên liệu E, tính bằng số kilômét đi được trên một lít xăng (km/l), của một mẫu xe ô tô được mô hình hóa theo tốc độ v (km/h) bằng công thức sau: E(v)=-0.00025v² + 0.003v² + 13.5. Mô hình này được áp dụng cho các tốc độ v từ 20km/h đến 120km/h (20≤v≤120). Tìm giá trị nhiên liệu hiệu quả nhất (tức là khi được nhiều kilômét nhất trên một lít xăng, làm tròn hàng phần mười).
Câu 5. Đều đặn ngày đầu mỗi tháng, anh Hùng gửi 10 triệu đồng tiết kiệm ở một ngân hàng theo hình thức lãi kép, kỳ hạn 1 tháng với lãi suất tiết kiệm là 4%/năm. Sau khi gửi được 12 tháng, kể từ tháng thứ 13, ngân hàng thay đổi lãi suất tiền gửi lên mức 5%/năm với kỳ hạn 1 tháng (số tiền gửi cũ sẽ được tính theo lãi suất mới kể từ tháng thứ 13). Anh Hùng tiếp tục gửi 10 triệu đồng vào ngày đầu mỗi tháng từ tháng thứ 13 đến tháng thứ 24. Đầu tháng thứ 25 anh Hùng quyết định rút toàn bộ số tiền (cả gốc và lãi) ra để đầu tư kinh doanh. Hỏi tổng số tiền anh Hùng nhận được là bao nhiêu triệu đồng (làm tròn kết quả đến hàng đơn vị)?
Câu 6. Các nhà nghiên cứu về tâm lý học giáo dục quan sát một nhóm các học sinh lớp 10 ở một số trường học THPT trong 3 năm. Ở thời điểm bắt đầu quan sát, có 69% số học sinh được quan sát thường xuyên sử dụng điện thoại thông minh. Sau 3 năm, các nhà nghiên cứu say minh thấy tỉ lệ học sinh có kết quả học tập sa sút trong số những học sinh thường xuyên sử dụng điện thoại thông minh cao gấp 3 lần tỉ lệ này trong số những học sinh còn lại. Chọn ngẫu nhiên một học sinh trong nhóm và thấy học sinh này có kết quả học tập sa sút trong 3 năm quan sát, tính xác suất để học sinh này thường xuyên sử dụng điện thoại thông minh (làm tròn kết quả đến hàng phần trăm).
Câu 1. Trong không gian Oxyz, phương trình của đường thẳng đi qua A(-1,-1,1) và có vectơ chỉ phương $\vec{u}(1,2,3)$ là
A. $\frac{x-1}{-1} = \frac{y-2}{-1} = \frac{z-3}{1}$.
B. $\frac{x+1}{-1} = \frac{y+2}{-1} = \frac{z+3}{1}$.
C. $\frac{x+1}{1} = \frac{y+1}{2} = \frac{z-1}{3}$.
D. $\frac{x-1}{1} = \frac{y-1}{2} = \frac{z+1}{3}$.
Câu 2. Hai mẫu số liệu ghép nhóm $M_1$, $M_2$ có bảng tần số ghép nhóm như sau:

Gọi $s_1^2$, $s_2^2$ lần lượt là phương sai của mẫu số liệu ghép nhóm $M_1$, $M_2$. Phát biểu nào sau đây là đúng?
A. $s_1^2 = 3s_2^2$.
B. $3s_1^2 = s_2^2$.
C. $s_1^2 = 9s_2^2$.
D. $s_1^2 = s_2^2$.
Câu 3. Cho $\int_0^2 f(x)dx = 1$ và $\int_2^5 f(x)dx = 3$. Tính $\int_0^5 f(x)dx$.
A. $\int_0^5 f(x)dx = -2$.
B. $\int_0^5 f(x)dx = -3$.
C. $\int_0^5 f(x)dx = 2$.
D. $\int_0^5 f(x)dx = 4$.
Câu 4. Với $a$ là số thực dương thì $\log_a(3a)$ bằng
A. $a$.
B. $1-\log_a a$.
C. $1+\log_a a$.
D. $1+a$.
Câu 5. Cho cấp số nhân $(u_n)$ có $u_1 = 1$ và công bội $q = 2$. Tổng năm số hạng đầu tiên của cấp số nhân là
A. 16.
B. 25.
C. 31.
D. 32.
Câu 6. Hàm số nào sau đây có đồ thị như hình vẽ?

A. $y = \frac{x-2}{x+1}$.
B. $y = \frac{x^2+2x+2}{x+1}$.
C. $y = x^2-2x+3$.
D. $y = x^2-3x+2$.
Câu 7. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình $(x-1)^2+(y+2)^2+(z-3)^2 = 4$. Tâm I của mặt cầu (S) có tọa độ là
A. $I(-1;2;3)$.
B. $I(-1;2;-3)$.
C. $I(1;-2;-3)$.
D. $I(1;-2;3)$.
Câu 8. Cho hình hộp chữ nhật $ABCD.A'B'C'D'$.

Mệnh đề nào sau đây đúng?
A. $\overrightarrow{AB}.\overrightarrow{AA'}= 0$.
B. $\overrightarrow{AB}.\overrightarrow{AC'}= 0$.
C. $\overrightarrow{AB}.\overrightarrow{BA'}= 0$.
D. $\overrightarrow{AB}.\overrightarrow{AC}= 0$.
Câu 9. Tập xác định của hàm số $y = \log_{\frac{1}{2}} x$ là
A. $(0; +\infty)$.
B. $(-\infty; 0)$.
C. $(-\infty; +\infty)$.
D. $[0; +\infty)$.
Câu 10. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ:

Hàm số nghịch biến trên khoảng nào dưới đây?
A. $(-\infty; -1)$.
B. $(4; +\infty)$.
C. $(-1;1)$.
D. $(0;1)$.
Câu 11. Cho hai biến cố $A$ và $B$ độc lập với nhau. Biết $P(A) = 0{,}4$ và $P(B) = 0{,}5$. Tính $P(AB)$.
A. 0,1.
B. 0,8.
C. 0,2.
D. 0,9.
Câu 12. Mệnh đề nào sau đây đúng?
A. $\left( \int \sin x \, dx \right)' = \sin x$.
B. $\left( \int \sin x \, dx \right)' = -\cos x + c$.
C. $\left( \int \sin x \, dx \right)' = \cos x$.
D. $\left( \int \sin x \, dx \right)' = -\cos x$.
PHẦN II. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.Câu 1. Một doanh nghiệp sản xuất thực phẩm – đồ uống có tiền lương hàng tháng của các nhân viên được thống kê bởi bảng sau:
| Lương tháng (triệu đồng) | [5; 10) | [10; 15) | [15; 20) | [20; 25) | [25; 30] | |
| Số nhân viên | 8 | 10 | 16 | 12 | 2 | n = 48 |
a) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là $\Delta_Q = Q_3 - Q_1$.
b) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên là $Q_3 = 20{,}833$.
c) Có ít nhất 75% nhân viên của doanh nghiệp có mức lương hàng tháng không vượt quá 17 triệu đồng.
d) Nếu một nhân viên của doanh nghiệp có mức lương là 34 triệu đồng / tháng thì lương của nhân viên này là một giá trị ngoại lệ.
Câu 2. Một trang trại cần xây một bể chứa nước hình trụ bằng bê tông (có nắp đậy) để chứa $60m^3$ nước tưới tiêu. Chi phí xây dựng chủ yếu phụ thuộc vào diện tích bề mặt bê tông cần sử dụng (diện tích toàn phần của bể tính theo phần bên trong của bể). Theo hợp đồng với nhà thầu xây dựng, chi phí mỗi mét vuông xây dựng theo cách tính trên là 1,5 triệu đồng. Gọi $r$ là bán kính đáy và $h$ là chiều cao của bể (đơn vị tính của $r, h$ là mét).
a) Thể tích của bể là: $V = \pi r^2 h = 60m^3$.
b) Diện tích toàn phần $S_p$ của bể chứa nước được biểu diễn theo bán kính $r$ là $S_p(r) = \pi r^2 + \frac{120}{r}$ (m²).
c) Để tiết kiệm chi phí nhất, bể nên được xây với bán kính đáy là $r = \sqrt{\frac{30}{\pi}}$ m.
d) Chi phí thấp nhất để xây dựng bể chứa nước nói trên là 127 triệu đồng (làm tròn kết quả đến hàng đơn vị).
Câu 3. Cho hàm số $f(x) = x^3 - 3x^2 + 2$ có đồ thị là đường cong $(C)$. Đường thẳng $d$ đi qua tâm đối xứng của $(C)$ và cắt $(C)$ tại hai điểm $A$ và $B$ (như hình vẽ). Biết điểm $A$ có hoành độ bằng -1.

a) Tọa độ tâm đối xứng của đồ thị hàm số $f(x)$ là $I(0;1)$.
b) Điểm $A$ có tung độ bằng $-2$.
c) Đường thẳng $d$ có phương trình là $y = x + 1$.
d) Diện tích hình phẳng giới hạn bởi đường cong $(C)$ và đường thẳng $d$ (phần gạch chéo) bằng 8.
Câu 4. Tại một nút giao thông của một khu vực đông dân cư với tốc độ tối đa cho phép đối với ô tô là 50 km/h, người ta gắn một camera phát nguội tại điểm $S(0; 0; 14)$ trong không gian $Oxyz$ (đơn vị trên mỗi trục tọa độ là mét), mặt phẳng $Oxy$ song song với mặt đường và chứa vùng nhận diện biển số xe của các phương tiện tham gia giao thông.
Biết rằng camera nhận diện tốt nhất biển số xe của các phương tiện tham gia giao thông là khi biển số của xe nằm trong hình thang cân $ABCD$ với: $SA = SB = 27$ m, $OD = OC = 5$ m, $AB = 14$ m, $CD = 9,6$ m và $AB \parallel CD$ nằm trên đường trung trực các đoạn thẳng $AB$ và $DC$ (xem hình vẽ minh họa).
Giả sử tại thời điểm 9h00' (được xem là thời điểm xuất phát) một ô tô chuyển động thẳng đều theo phương song song với trục $Ox$, hướng về phía trục $Oy$ và có vị trí của biển số xe là $M(50; -6; 0)$.

a) Điểm $D$ có tọa độ là $(1,4;\ -4,8;\ 0)$.
b) Đường thẳng $AD$ có phương trình là $ \begin{cases} x = 1,4 - 20,6t \\ y = -4,8 + 2,2t \ (t \in \mathbb{R}) \\ z = 0 \end{cases} $
c) Nếu ô tô đi với vận tốc 45 km/h thì sau đúng 2,2 giây kể từ thời điểm xuất phát thì biển số của xe ôtô đã nằm trong vùng nhận diện tốt nhất của camera.
d) Nếu camera ghi nhận được hình ảnh biển số xe ô tô liên tục trong một khoảng thời gian kéo dài đúng 0,7 giây, và khoảng thời gian 0,7 giây này kết thúc đồng thời với thời điểm xe vừa ra khỏi vùng nhận diện tốt nhất, thì ôtô đã vượt quá tốc độ cho phép.
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.Câu 1. Trong một cuộc diễn tập phòng không, một bệ phóng tên lửa phòng không được đặt tại vị trí $O\left(0; 0; 0\right)$ (trong không gian $Oxyz$ với đơn vị trên các hệ trục tính theo ki-lô-mét) có tầm bắn tối đa là 30 km và tên lửa được phóng ra với vận tốc không đổi là 500 m/s. Một máy bay không người lái bay theo một đường thẳng có vectơ chỉ phương $\vec{u} = (3; -4; 0)$ với vận tốc không đổi là 900 km/h. Khi phát hiện máy bay không người lái tại vị trí $A(6; -20; 16)$ thì tên lửa rời bệ phóng, khai hỏa và đã bắn hạ được mục tiêu. Hỏi khoảng cách từ bệ phóng tên lửa đến vị trí máy bay không người lái bị bắn hạ bằng bao nhiêu ki-lô-mét? (Giả sử cả máy bay không người lái và tên lửa đều bay theo đường thẳng và không chịu tác động của trọng lực hay lực cản không khí).
Câu 2. Một công ty thuê thợ vẽ logo công ty như hình vẽ lên một bức tường lớn. Logo có dạng là 1 bông hoa có 6 cánh hoa giống nhau, sắp xếp cách đều nhau như hình vẽ.

Để chính xác hóa kích thước và hình dạng khi vẽ, mỗi cánh hoa được thiết kế như sau: Trong mặt phẳng $Oxy$ (một đơn vị ứng với 1 mét trên thực tế), một cánh hoa được xem là một hình phẳng giới hạn bởi đồ thị hàm số bậc ba $y = \dfrac{(x - 3)^3}{27} + 1$ $(C)$ và một đường parabol $(P): y = ax^2 + bx + c \, (a \ne 0)$. $(C)$ và $(P)$ cắt nhau tại hai điểm $O(0;0), M(6;2)$ và $(P)$ đi qua điểm $N(3;0)$. Biết rằng chi phí vẽ logo nói trên được tính dựa trên mỗi mét vuông cánh hoa được vẽ, mỗi mét vuông được báo giá là 210 nghìn đồng. Hãy tính chi phí vẽ logo đó (đơn vị tính: nghìn đồng, làm tròn kết quả đến hàng đơn vị).
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB=2, AD=4 và SA⊥(ABCD). SA=2√5. Tính số đo góc giữa đường thẳng SC và mặt phẳng (SBD) (đơn vị đo góc: độ, làm tròn kết quả với hàng phần mười).
Câu 4. Hiệu quả nhiên liệu E, tính bằng số kilômét đi được trên một lít xăng (km/l), của một mẫu xe ô tô được mô hình hóa theo tốc độ v (km/h) bằng công thức sau: E(v)=-0.00025v² + 0.003v² + 13.5. Mô hình này được áp dụng cho các tốc độ v từ 20km/h đến 120km/h (20≤v≤120). Tìm giá trị nhiên liệu hiệu quả nhất (tức là khi được nhiều kilômét nhất trên một lít xăng, làm tròn hàng phần mười).
Câu 5. Đều đặn ngày đầu mỗi tháng, anh Hùng gửi 10 triệu đồng tiết kiệm ở một ngân hàng theo hình thức lãi kép, kỳ hạn 1 tháng với lãi suất tiết kiệm là 4%/năm. Sau khi gửi được 12 tháng, kể từ tháng thứ 13, ngân hàng thay đổi lãi suất tiền gửi lên mức 5%/năm với kỳ hạn 1 tháng (số tiền gửi cũ sẽ được tính theo lãi suất mới kể từ tháng thứ 13). Anh Hùng tiếp tục gửi 10 triệu đồng vào ngày đầu mỗi tháng từ tháng thứ 13 đến tháng thứ 24. Đầu tháng thứ 25 anh Hùng quyết định rút toàn bộ số tiền (cả gốc và lãi) ra để đầu tư kinh doanh. Hỏi tổng số tiền anh Hùng nhận được là bao nhiêu triệu đồng (làm tròn kết quả đến hàng đơn vị)?
Câu 6. Các nhà nghiên cứu về tâm lý học giáo dục quan sát một nhóm các học sinh lớp 10 ở một số trường học THPT trong 3 năm. Ở thời điểm bắt đầu quan sát, có 69% số học sinh được quan sát thường xuyên sử dụng điện thoại thông minh. Sau 3 năm, các nhà nghiên cứu say minh thấy tỉ lệ học sinh có kết quả học tập sa sút trong số những học sinh thường xuyên sử dụng điện thoại thông minh cao gấp 3 lần tỉ lệ này trong số những học sinh còn lại. Chọn ngẫu nhiên một học sinh trong nhóm và thấy học sinh này có kết quả học tập sa sút trong 3 năm quan sát, tính xác suất để học sinh này thường xuyên sử dụng điện thoại thông minh (làm tròn kết quả đến hàng phần trăm).
