Tham khảo đề khảo sát chất lượng Toán 12 lần 2 năm học 2024 – 2025 do Sở GD&ĐT Phú Thọ ra đề. Có đáp án và lời giải chi tiết giúp học sinh ôn luyện thi tốt nghiệp THPT hiệu quả.
Câu 1. Trong không gian \( Oxyz \), cho mặt cầu \( (S) \) có phương trình: $ (x - 2)^2 + (y + 1)^2 + (z - 3)^2 = 9. $ Tọa độ tâm của mặt cầu đã cho là
A. \( (2; -1; 3) \)
B. \( (-2; 1; 3) \)
C. \( (-2; 1; -3) \)
D. \( (-2; -1; 3) \)
Câu 2. Họ các nguyên hàm của hàm số \( f(x) = 2^x \) là
A. \( \frac{2^x}{\ln 2} + C \)
B. \( 2^x \ln 2 + C \)
C. \( x \cdot 2^{x - 1} + C \)
D. \( 2^x \ln x + C \)
Câu 3. Cho hàm số \( y = \frac{ax + b}{cx + d} \quad (a, b, c, d \in \mathbb{R}) \) có đồ thị là đường cong như hình vẽ.
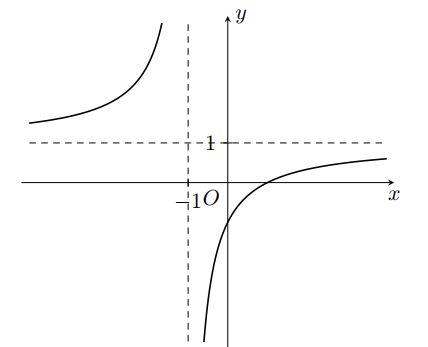
Tọa độ tâm đối xứng của đồ thị hàm số đã cho là
A. \( (-1;1) \).
B. \( (1;1) \).
C. \( (1;-1) \).
D. \( (0;1) \).
Câu 4. Hai mẫu số liệu ghép nhóm \( A, B \) có bảng tần số ghép nhóm như sau:
Nhóm A
Nhóm B
Gọi \( \Delta_{Q_A}, \Delta_{Q_B} \) lần lượt là khoảng tứ phân vị của mẫu số liệu ghép nhóm \( A, B \). Phát biểu nào sau đây đúng?
A. \( \Delta_{Q_B} = 2 \Delta_{Q_A} \).
B. \( \Delta_{Q_B} = 0{,}3 + \Delta_{Q_A} \).
C. \( \Delta_{Q_B} = \Delta_{Q_A} \).
D. \( \Delta_{Q_B} = 0{,}3 \Delta_{Q_A} \).
Câu 5. Số nghiệm của phương trình \( \log(2x - 1) = \log(x^2 - 4) \) là
A. 2.
B. 0.
C. 1.
D. 3.
Câu 6. Nếu \( \int_a^b f(x)\,dx = 2025 \) thì \( \int_a^b 2f(x)\,dx \) bằng
A. \( 2025^2 \).
B. \( \dfrac{2025}{2} \).
C. 2023.
D. 4050.
Câu 7. Cho hàm số bậc ba \( y = f(x) \) có đồ thị như hình vẽ.
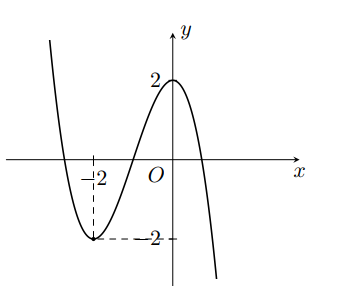
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. \( (-\infty; -2) \).
B. \( (-2; 0) \).
C. \( (0; +\infty) \).
D. \( (-1; 1) \).
Câu 8. Cho cấp số nhân \( (u_n) \) có \( u_1 = 1, u_4 = 27 \). Công bội \( q \) của cấp số nhân đã cho bằng
A. \( \dfrac{26}{3} \).
B. \( \pm 3 \).
C. \( -3 \).
D. 3.
Câu 9. Cho hình chóp \( S.ABCD \) có đáy \( ABCD \) là hình vuông và \( SA \) vuông góc với mặt phẳng đáy. Đường thẳng \( CD \) vuông góc với mặt phẳng nào dưới đây?
A. \( (SAC) \).
B. \( (SAD) \).
C. \( (SAB) \).
D. \( (SBC) \).
Câu 10. Cho tứ diện \( S.ABC \) với \( M, N, P \) lần lượt là trung điểm của \( SA, SB, SC \) (tham khảo hình vẽ).
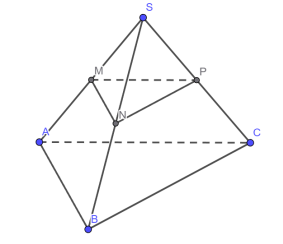
Khẳng định nào sau đây đúng?
A. \( \overrightarrow{AB} = \dfrac{1}{2}(\overrightarrow{PN} - \overrightarrow{PM}) \).
B. \( \overrightarrow{AB} = \overrightarrow{PN} - \overrightarrow{PM} \).
C. \( \overrightarrow{AB} = 2(\overrightarrow{PN} - \overrightarrow{PM}) \).
D. \( \overrightarrow{AB} = 2(\overrightarrow{PM} - \overrightarrow{PN}) \).
Câu 11. Tập nghiệm của phương trình \( (0,2)^x \leq 4 \) là
A. \( (-\infty; \log_4 0{,}2] \).
B. \( [\log_{0,2} 4; +\infty) \).
C. \( (-\infty; \log_{0,2} 4] \).
D. \( [\log_4 0{,}2; +\infty) \).
Câu 12. Trong không gian \( Oxyz \), cho mặt phẳng \( (P) \) có phương trình: \( 2x - y + z - 4 = 0 \). Phương trình mặt phẳng \( (Q) \) song song với \( (P) \) và đi qua điểm \( M(1; -1; 3) \) là
A. \( 2x - y + z + 6 = 0 \).
B. \( 2x + 3y - z + 4 = 0 \).
C. \( 2x - y + z - 6 = 0 \).
D. \( x - y + 3z - 6 = 0 \).
Câu 1. Cây cà chua khi trồng có chiều cao 5 cm. Tốc độ tăng chiều cao của cây cà chua sau khi trồng được cho bởi hàm số \( v(t) = -0{,}1t^3 + t^2 \), trong đó \( t \) tính theo tuần, \( v(t) \) tính bằng cm/tuần. Gọi \( h(t) \) (tính bằng cm) là độ cao của cây cà chua ở tuần thứ \( t \) (Nguồn: A. Bigalke et al., Grundkurs ma-1, Cornelsen 2016).
a) \( h'(t) = v(t) \).
b) \( h(t) = -\dfrac{t^4}{40} + \dfrac{t^3}{3} + 5, t \geq 0 \).
c) Giai đoạn tăng chiều cao của cây cà chua kéo dài 9 tuần.
d) Chiều cao tối đa của cây cà chua (kết quả làm tròn đến hàng phần chục) bằng 88,3 cm.
Câu 2. Cho hàm số \( f(x) = 2\sin x + \sqrt{3x} \).
a) \( f(0) = 0, \, f(\pi) = \sqrt{3\pi} \).
b) Đạo hàm của hàm số đã cho là \( f'(x) = -2\cos x + \dfrac{\sqrt{3}}{2\sqrt{x}} \).
c) Nghiệm của phương trình \( f'(x) = 0 \) trên đoạn \([0; \pi]\) là \( x = \dfrac{\pi}{6} \).
d) Giá trị lớn nhất của hàm số \( f(x) \) trên đoạn \([0; \pi]\) bằng \( 1 + \dfrac{5\sqrt{3\pi}}{6} \).
Câu 3. Đường ống dẫn dầu trên không là hệ thống đường ống được treo trên các giá đỡ hoặc cột cao, dùng để vận chuyển dầu thô hoặc các sản phẩm dầu mỏ từ nơi này đến nơi khác mà không cần chôn dưới lòng đất. Hệ thống này thường được sử dụng trong các khu vực có địa hình khó khăn, vùng băng giá, rừng rậm..., những nơi mà việc đào đường ống ngầm không khả thi.

Với hệ trục toạ độ \(Oxyz\) thích hợp, mặt đất là mặt phẳng \(Oxy\), đơn vị trên mỗi trục là mét, người ta thiết lập một đường ống dẫn dầu trên không dọc theo đường thẳng \(d\) : $ \begin{cases} x = 0 \\ y = t \\ z = 20 \end{cases} \quad (t \text{ là tham số}). $
Vì địa hình phức tạp, người ta chọn điểm \(A(15;10;15)\) để làm điểm trung chuyển dầu từ mặt đất đến đường ống này.
a) Đường thẳng \(d\) nằm trên mặt phẳng \((Oyz)\).
b) Điểm đối xứng với \(A\) qua mặt phẳng \((Oxy)\) có toạ độ \(A'(-15;-10;15)\).
c) Do thực tế công việc, người ta cần xác định vị trí điểm \(B(0;b;20)\) thuộc đường ống và vị trí điểm \(C(m;n;0)\) thuộc mặt đất sao cho tổng độ dài các đoạn đường \(AB\), \(BC\), \(AC\) nhỏ nhất. Ta có \(m+n+b = \dfrac{200}{7}\).
d) Giá trị nhỏ nhất của tổng độ dài các đoạn đường \(AB\), \(BC\), \(AC\) làm tròn đến hàng phần chục bằng 45,5 m.
Câu 4. Giả sử có một đồng xu cân bằng (fair coin) và một đồng xu thiên lệch (biased coin) mà mặt ngửa (heads) xuất hiện với xác suất \(\dfrac{3}{4}\). Một người chơi chọn ngẫu nhiên một trong hai đồng xu và tung nó ba lần. Gọi \(A\) là biến cố: “Người chơi chọn đồng xu cân bằng”; \(B\) là biến cố: “Ba lần tung đồng xu đều xuất hiện mặt ngửa”.
a) \(P(A) = \dfrac{1}{2}\).
b) \(P(B \mid A) = \dfrac{3}{8}\).
c) Xác suất người đó chọn được đồng xu cân bằng biết rằng kết quả ba lần tung đồng xu đều xuất hiện mặt ngửa là 0,25 (kết quả làm tròn đến hàng phần trăm).
d) Biết rằng đồng xu được chọn tung ba lần đều xuất hiện mặt ngửa, xác suất người chơi đó tung lần thứ tư tiếp tục xuất hiện mặt ngửa là 0,69 (kết quả làm tròn đến hàng phần trăm).
Câu 2. Cho hình chóp \( S.ABC \) có đáy \( ABC \) là tam giác vuông cân tại \( C \) và \( AC = 4 \). Biết \( SA \) vuông góc với mặt phẳng đáy và khoảng cách từ \( A \) đến mặt phẳng \( (SBC) \) bằng \( \dfrac{12}{5} \). Thể tích của khối chóp \( S.ABC \) bằng bao nhiêu?
Câu 3. Một bức tường hình chữ nhật \( ABCD \) có kích thước lần lượt 6 m và 4 m được bạn Minh trang trí bằng cách vẽ hai đồ thị hàm số \( f(x) = a^x \ (0 < a \ne 1) \) và \( g(x) = \log_a x \ (0 < b \ne 1) \) đối xứng nhau qua đường thẳng \( y = x \). Bức tường được chia thành ba phần (tham khảo hình vẽ).
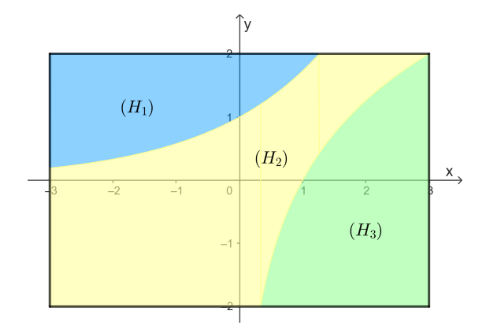
Phần \( H_1 \) được sơn màu xanh da trời, phần \( H_2 \) sơn màu vàng và phần \( H_3 \) được sơn màu xanh lá cây. Bạn Minh cần mua các hộp sơn mà mỗi hộp chỉ sơn được một màu tương ứng với các màu mà bạn Minh định sơn. Biết rằng mỗi hộp sơn chỉ sơn được tối đa 3 m² tường, giá một hộp sơn màu xanh da trời là 120000 đồng, giá một hộp sơn màu xanh lá cây là 140000 đồng, giá một hộp sơn màu vàng là 160000 đồng. Cửa hàng chỉ bán số các hộp sơn là các số nguyên dương. Bạn Minh cần bao nhiêu triệu đồng mua sơn để trang trí cho bức tường đó?
Câu 4. Trong một đợt diễn tập quốc phòng, hai người ở hai vị trí khác nhau cùng ngắm bắn một mục tiêu cố định trên không. Người ta gắn một hệ trục tọa độ \( Oxyz \) (đơn vị trên mỗi trục tính theo mét), mặt phẳng \( (Oxy) \) trùng với mặt đất. Người thứ nhất bắn một viên đạn đi qua hai điểm \( A(5;7;10) \) và \( B(6;9;12) \).
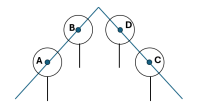
Người thứ hai bắn một viên đạn đi qua hai điểm \( C(15;17;5) \) và \( D \) (điểm \( D \) ở độ cao 26 m so với mặt đất).
Biết rằng sau một thời gian rời khỏi nòng súng, hai viên đạn va chạm với nhau tại vị trí cách điểm A một khoảng 150 m (tham khảo hình vẽ).
Hỏi \( D \) cách \( C \) một khoảng bao nhiêu mét? (Kết quả làm tròn đến hàng phần chục).
Câu 5. Xác suất bé An được mẹ dẫn theo khi đi mua sắm là \( \dfrac{2}{5} \). Khi bé An được đi theo mẹ thì 70% bé sẽ được mua đồ chơi. Khi bé không đi theo mẹ, có thể mẹ vẫn mua đồ chơi cho bé. Xác suất bé được đi theo mẹ biết rằng bé được mẹ mua cho đồ chơi là \( \dfrac{14}{23} \). Khi bé không đi theo mẹ, xác suất bé được mẹ mua cho đồ chơi là bao nhiêu?
Câu 6. Nhà máy \( A \) chuyên sản xuất một loại sản phẩm cung cấp cho nhà máy \( B \). Hai nhà máy thỏa thuận, mỗi tháng \( A \) cung cấp cho \( B \) tối đa 45 tấn sản phẩm và nếu số lượng đặt hàng là \( x \) tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm là \( P(x) = 60 - 0{,}01x^2 \) (triệu đồng). Chi phí để nhà máy \( A \) sản xuất \( x \) tấn sản phẩm trong một tháng là \( C(x) = 150 + 33x \) (triệu đồng) (gồm 150 triệu đồng chi phí cố định và 33 triệu đồng cho mỗi tấn sản phẩm). Để mỗi tháng thu được lợi nhuận lớn nhất thì \( A \) cần bán cho \( B \) bao nhiêu tấn sản phẩm?
Phần I. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.Câu 1. Trong không gian \( Oxyz \), cho mặt cầu \( (S) \) có phương trình: $ (x - 2)^2 + (y + 1)^2 + (z - 3)^2 = 9. $ Tọa độ tâm của mặt cầu đã cho là
A. \( (2; -1; 3) \)
B. \( (-2; 1; 3) \)
C. \( (-2; 1; -3) \)
D. \( (-2; -1; 3) \)
Câu 2. Họ các nguyên hàm của hàm số \( f(x) = 2^x \) là
A. \( \frac{2^x}{\ln 2} + C \)
B. \( 2^x \ln 2 + C \)
C. \( x \cdot 2^{x - 1} + C \)
D. \( 2^x \ln x + C \)
Câu 3. Cho hàm số \( y = \frac{ax + b}{cx + d} \quad (a, b, c, d \in \mathbb{R}) \) có đồ thị là đường cong như hình vẽ.

Tọa độ tâm đối xứng của đồ thị hàm số đã cho là
A. \( (-1;1) \).
B. \( (1;1) \).
C. \( (1;-1) \).
D. \( (0;1) \).
Câu 4. Hai mẫu số liệu ghép nhóm \( A, B \) có bảng tần số ghép nhóm như sau:
Nhóm A
| Nhóm | [0; 10) | [10; 20) | [20; 30) | [30; 40) | [40; 50) |
|---|---|---|---|---|---|
| Tần số | 8 | 9 | 5 | 6 | 2 |
| Nhóm | [0; 3,10; 3) | [10; 3; 20; 3) | [20; 3; 30; 3) | [30; 3; 40; 3) | [40; 3; 50; 3) |
|---|---|---|---|---|---|
| Tần số | 16 | 18 | 12 | 10 | 4 |
A. \( \Delta_{Q_B} = 2 \Delta_{Q_A} \).
B. \( \Delta_{Q_B} = 0{,}3 + \Delta_{Q_A} \).
C. \( \Delta_{Q_B} = \Delta_{Q_A} \).
D. \( \Delta_{Q_B} = 0{,}3 \Delta_{Q_A} \).
Câu 5. Số nghiệm của phương trình \( \log(2x - 1) = \log(x^2 - 4) \) là
A. 2.
B. 0.
C. 1.
D. 3.
Câu 6. Nếu \( \int_a^b f(x)\,dx = 2025 \) thì \( \int_a^b 2f(x)\,dx \) bằng
A. \( 2025^2 \).
B. \( \dfrac{2025}{2} \).
C. 2023.
D. 4050.
Câu 7. Cho hàm số bậc ba \( y = f(x) \) có đồ thị như hình vẽ.

Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. \( (-\infty; -2) \).
B. \( (-2; 0) \).
C. \( (0; +\infty) \).
D. \( (-1; 1) \).
Câu 8. Cho cấp số nhân \( (u_n) \) có \( u_1 = 1, u_4 = 27 \). Công bội \( q \) của cấp số nhân đã cho bằng
A. \( \dfrac{26}{3} \).
B. \( \pm 3 \).
C. \( -3 \).
D. 3.
Câu 9. Cho hình chóp \( S.ABCD \) có đáy \( ABCD \) là hình vuông và \( SA \) vuông góc với mặt phẳng đáy. Đường thẳng \( CD \) vuông góc với mặt phẳng nào dưới đây?
A. \( (SAC) \).
B. \( (SAD) \).
C. \( (SAB) \).
D. \( (SBC) \).
Câu 10. Cho tứ diện \( S.ABC \) với \( M, N, P \) lần lượt là trung điểm của \( SA, SB, SC \) (tham khảo hình vẽ).

Khẳng định nào sau đây đúng?
A. \( \overrightarrow{AB} = \dfrac{1}{2}(\overrightarrow{PN} - \overrightarrow{PM}) \).
B. \( \overrightarrow{AB} = \overrightarrow{PN} - \overrightarrow{PM} \).
C. \( \overrightarrow{AB} = 2(\overrightarrow{PN} - \overrightarrow{PM}) \).
D. \( \overrightarrow{AB} = 2(\overrightarrow{PM} - \overrightarrow{PN}) \).
Câu 11. Tập nghiệm của phương trình \( (0,2)^x \leq 4 \) là
A. \( (-\infty; \log_4 0{,}2] \).
B. \( [\log_{0,2} 4; +\infty) \).
C. \( (-\infty; \log_{0,2} 4] \).
D. \( [\log_4 0{,}2; +\infty) \).
Câu 12. Trong không gian \( Oxyz \), cho mặt phẳng \( (P) \) có phương trình: \( 2x - y + z - 4 = 0 \). Phương trình mặt phẳng \( (Q) \) song song với \( (P) \) và đi qua điểm \( M(1; -1; 3) \) là
A. \( 2x - y + z + 6 = 0 \).
B. \( 2x + 3y - z + 4 = 0 \).
C. \( 2x - y + z - 6 = 0 \).
D. \( x - y + 3z - 6 = 0 \).
Phần II. Thí sinh trả lời từ câu 1 đến câu 4
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.Câu 1. Cây cà chua khi trồng có chiều cao 5 cm. Tốc độ tăng chiều cao của cây cà chua sau khi trồng được cho bởi hàm số \( v(t) = -0{,}1t^3 + t^2 \), trong đó \( t \) tính theo tuần, \( v(t) \) tính bằng cm/tuần. Gọi \( h(t) \) (tính bằng cm) là độ cao của cây cà chua ở tuần thứ \( t \) (Nguồn: A. Bigalke et al., Grundkurs ma-1, Cornelsen 2016).
a) \( h'(t) = v(t) \).
b) \( h(t) = -\dfrac{t^4}{40} + \dfrac{t^3}{3} + 5, t \geq 0 \).
c) Giai đoạn tăng chiều cao của cây cà chua kéo dài 9 tuần.
d) Chiều cao tối đa của cây cà chua (kết quả làm tròn đến hàng phần chục) bằng 88,3 cm.
Câu 2. Cho hàm số \( f(x) = 2\sin x + \sqrt{3x} \).
a) \( f(0) = 0, \, f(\pi) = \sqrt{3\pi} \).
b) Đạo hàm của hàm số đã cho là \( f'(x) = -2\cos x + \dfrac{\sqrt{3}}{2\sqrt{x}} \).
c) Nghiệm của phương trình \( f'(x) = 0 \) trên đoạn \([0; \pi]\) là \( x = \dfrac{\pi}{6} \).
d) Giá trị lớn nhất của hàm số \( f(x) \) trên đoạn \([0; \pi]\) bằng \( 1 + \dfrac{5\sqrt{3\pi}}{6} \).
Câu 3. Đường ống dẫn dầu trên không là hệ thống đường ống được treo trên các giá đỡ hoặc cột cao, dùng để vận chuyển dầu thô hoặc các sản phẩm dầu mỏ từ nơi này đến nơi khác mà không cần chôn dưới lòng đất. Hệ thống này thường được sử dụng trong các khu vực có địa hình khó khăn, vùng băng giá, rừng rậm..., những nơi mà việc đào đường ống ngầm không khả thi.

Với hệ trục toạ độ \(Oxyz\) thích hợp, mặt đất là mặt phẳng \(Oxy\), đơn vị trên mỗi trục là mét, người ta thiết lập một đường ống dẫn dầu trên không dọc theo đường thẳng \(d\) : $ \begin{cases} x = 0 \\ y = t \\ z = 20 \end{cases} \quad (t \text{ là tham số}). $
Vì địa hình phức tạp, người ta chọn điểm \(A(15;10;15)\) để làm điểm trung chuyển dầu từ mặt đất đến đường ống này.
a) Đường thẳng \(d\) nằm trên mặt phẳng \((Oyz)\).
b) Điểm đối xứng với \(A\) qua mặt phẳng \((Oxy)\) có toạ độ \(A'(-15;-10;15)\).
c) Do thực tế công việc, người ta cần xác định vị trí điểm \(B(0;b;20)\) thuộc đường ống và vị trí điểm \(C(m;n;0)\) thuộc mặt đất sao cho tổng độ dài các đoạn đường \(AB\), \(BC\), \(AC\) nhỏ nhất. Ta có \(m+n+b = \dfrac{200}{7}\).
d) Giá trị nhỏ nhất của tổng độ dài các đoạn đường \(AB\), \(BC\), \(AC\) làm tròn đến hàng phần chục bằng 45,5 m.
Câu 4. Giả sử có một đồng xu cân bằng (fair coin) và một đồng xu thiên lệch (biased coin) mà mặt ngửa (heads) xuất hiện với xác suất \(\dfrac{3}{4}\). Một người chơi chọn ngẫu nhiên một trong hai đồng xu và tung nó ba lần. Gọi \(A\) là biến cố: “Người chơi chọn đồng xu cân bằng”; \(B\) là biến cố: “Ba lần tung đồng xu đều xuất hiện mặt ngửa”.
a) \(P(A) = \dfrac{1}{2}\).
b) \(P(B \mid A) = \dfrac{3}{8}\).
c) Xác suất người đó chọn được đồng xu cân bằng biết rằng kết quả ba lần tung đồng xu đều xuất hiện mặt ngửa là 0,25 (kết quả làm tròn đến hàng phần trăm).
d) Biết rằng đồng xu được chọn tung ba lần đều xuất hiện mặt ngửa, xác suất người chơi đó tung lần thứ tư tiếp tục xuất hiện mặt ngửa là 0,69 (kết quả làm tròn đến hàng phần trăm).
Phần III. Thí sinh trả lời từ câu 1 đến câu 6
Câu 1. Để tiết kiệm tiền sau này cho việc học đại học của con, cô Bình quyết định gửi 1,5 triệu đồng cuối mỗi tháng vào ngân hàng với lãi suất mỗi tháng là 0,3% theo hình thức lãi kép. Cô bắt đầu gửi tiền khi con cô tròn 3 tuổi. Cô Bình sẽ tiết kiệm được bao nhiêu tiền vào thời điểm con cô tròn 18 tuổi nếu cô không rút lãi và lãi suất ngân hàng không thay đổi trong suốt quá trình gửi tiết kiệm? (Kết quả làm tròn đến hàng đơn vị theo triệu đồng).Câu 2. Cho hình chóp \( S.ABC \) có đáy \( ABC \) là tam giác vuông cân tại \( C \) và \( AC = 4 \). Biết \( SA \) vuông góc với mặt phẳng đáy và khoảng cách từ \( A \) đến mặt phẳng \( (SBC) \) bằng \( \dfrac{12}{5} \). Thể tích của khối chóp \( S.ABC \) bằng bao nhiêu?
Câu 3. Một bức tường hình chữ nhật \( ABCD \) có kích thước lần lượt 6 m và 4 m được bạn Minh trang trí bằng cách vẽ hai đồ thị hàm số \( f(x) = a^x \ (0 < a \ne 1) \) và \( g(x) = \log_a x \ (0 < b \ne 1) \) đối xứng nhau qua đường thẳng \( y = x \). Bức tường được chia thành ba phần (tham khảo hình vẽ).

Phần \( H_1 \) được sơn màu xanh da trời, phần \( H_2 \) sơn màu vàng và phần \( H_3 \) được sơn màu xanh lá cây. Bạn Minh cần mua các hộp sơn mà mỗi hộp chỉ sơn được một màu tương ứng với các màu mà bạn Minh định sơn. Biết rằng mỗi hộp sơn chỉ sơn được tối đa 3 m² tường, giá một hộp sơn màu xanh da trời là 120000 đồng, giá một hộp sơn màu xanh lá cây là 140000 đồng, giá một hộp sơn màu vàng là 160000 đồng. Cửa hàng chỉ bán số các hộp sơn là các số nguyên dương. Bạn Minh cần bao nhiêu triệu đồng mua sơn để trang trí cho bức tường đó?
Câu 4. Trong một đợt diễn tập quốc phòng, hai người ở hai vị trí khác nhau cùng ngắm bắn một mục tiêu cố định trên không. Người ta gắn một hệ trục tọa độ \( Oxyz \) (đơn vị trên mỗi trục tính theo mét), mặt phẳng \( (Oxy) \) trùng với mặt đất. Người thứ nhất bắn một viên đạn đi qua hai điểm \( A(5;7;10) \) và \( B(6;9;12) \).

Người thứ hai bắn một viên đạn đi qua hai điểm \( C(15;17;5) \) và \( D \) (điểm \( D \) ở độ cao 26 m so với mặt đất).
Biết rằng sau một thời gian rời khỏi nòng súng, hai viên đạn va chạm với nhau tại vị trí cách điểm A một khoảng 150 m (tham khảo hình vẽ).
Hỏi \( D \) cách \( C \) một khoảng bao nhiêu mét? (Kết quả làm tròn đến hàng phần chục).
Câu 5. Xác suất bé An được mẹ dẫn theo khi đi mua sắm là \( \dfrac{2}{5} \). Khi bé An được đi theo mẹ thì 70% bé sẽ được mua đồ chơi. Khi bé không đi theo mẹ, có thể mẹ vẫn mua đồ chơi cho bé. Xác suất bé được đi theo mẹ biết rằng bé được mẹ mua cho đồ chơi là \( \dfrac{14}{23} \). Khi bé không đi theo mẹ, xác suất bé được mẹ mua cho đồ chơi là bao nhiêu?
Câu 6. Nhà máy \( A \) chuyên sản xuất một loại sản phẩm cung cấp cho nhà máy \( B \). Hai nhà máy thỏa thuận, mỗi tháng \( A \) cung cấp cho \( B \) tối đa 45 tấn sản phẩm và nếu số lượng đặt hàng là \( x \) tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm là \( P(x) = 60 - 0{,}01x^2 \) (triệu đồng). Chi phí để nhà máy \( A \) sản xuất \( x \) tấn sản phẩm trong một tháng là \( C(x) = 150 + 33x \) (triệu đồng) (gồm 150 triệu đồng chi phí cố định và 33 triệu đồng cho mỗi tấn sản phẩm). Để mỗi tháng thu được lợi nhuận lớn nhất thì \( A \) cần bán cho \( B \) bao nhiêu tấn sản phẩm?
