PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn ( 3 điểm)
Câu 1.Cho cấp số cộng $\left( {{u}_{n}} \right)$, biết ${{u}_{2}}=3$ và ${{u}_{4}}=7$. Giá trị của ${{u}_{15}}$ bằngA. $27$.
B. $31$.
C. $35$.
D. $29$.
Chọn D
Từ giả thiết ${{u}_{2}}=3$ và ${{u}_{4}}=7$ suy ra ta có hệ phương trình: $\left\{ \begin{align} & {{u}_{1}}+d=3 \\ & {{u}_{1}}+3d=7 \\ \end{align} \right.$$\Rightarrow \left\{ \begin{align} & {{u}_{1}}=1 \\ & d=2 \\ \end{align} \right.$.
Vậy ${{u}_{15}}={{u}_{1}}+14d=29$.
Từ giả thiết ${{u}_{2}}=3$ và ${{u}_{4}}=7$ suy ra ta có hệ phương trình: $\left\{ \begin{align} & {{u}_{1}}+d=3 \\ & {{u}_{1}}+3d=7 \\ \end{align} \right.$$\Rightarrow \left\{ \begin{align} & {{u}_{1}}=1 \\ & d=2 \\ \end{align} \right.$.
Vậy ${{u}_{15}}={{u}_{1}}+14d=29$.
A. ${{u}_{5}}=\frac{-27}{16}.$
B. ${{u}_{5}}=\frac{-16}{27}.$
C. ${{u}_{5}}=\frac{16}{27}.$
D. ${{u}_{5}}=\frac{27}{16}.$
Chọn B
Ta có: ${{u}_{5}}={{u}_{1}}.{{q}^{4}}=\left( -3 \right){{\left( \frac{2}{3} \right)}^{4}}=-\frac{16}{27}.$
Ta có: ${{u}_{5}}={{u}_{1}}.{{q}^{4}}=\left( -3 \right){{\left( \frac{2}{3} \right)}^{4}}=-\frac{16}{27}.$
A. Nếu $b//\left( \alpha \right)$ thì $b//a.$
B. Nếu $b$ cắt $\left( \alpha \right)$ thì $b$ cắt $a.$
C. Nếu $b//a$ thì $b//\left( \alpha \right).$
D. Nếu $b$ cắt $\left( \alpha \right)$ và $mp\left( \beta \right)$ chứa $b$ thì giao tuyến của $\left( \alpha \right)$ và $\left( \beta \right)$ là đường thẳng cắt cả $a$ và $b$.
Chọn C
Ta có: $\left. \begin{align} & a\subset \left( \alpha \right) \\ & b\not\subset \left( \alpha \right) \\ & a//b \\ \end{align} \right\}\Rightarrow b//\left( \alpha \right).$
Ta có: $\left. \begin{align} & a\subset \left( \alpha \right) \\ & b\not\subset \left( \alpha \right) \\ & a//b \\ \end{align} \right\}\Rightarrow b//\left( \alpha \right).$
A. $\frac{12}{36}$.
B. $\frac{11}{36}$.
C. $\frac{6}{36}$.
D. $\frac{8}{36}$.
.
Chọn B
$n(\Omega )=6.6=36$. Gọi $A$:”ít nhất một lần xuất hiện mặt sáu chấm”.
Khi đó $\overline{A}$:”không có lần nào xuất hiện mặt sáu chấm”.
Ta có$n(\overline{A})=5.5=25$. Vậy $P(A)=1-P(\overline{A})=1-\frac{25}{36}=\frac{11}{36}$.
Chọn B
$n(\Omega )=6.6=36$. Gọi $A$:”ít nhất một lần xuất hiện mặt sáu chấm”.
Khi đó $\overline{A}$:”không có lần nào xuất hiện mặt sáu chấm”.
Ta có$n(\overline{A})=5.5=25$. Vậy $P(A)=1-P(\overline{A})=1-\frac{25}{36}=\frac{11}{36}$.
A. $y=\frac{x+2}{x+1}$.
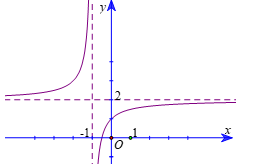
B. $y=\frac{2x+1}{x+1}$.
C. $y=\frac{x-1}{x+1}$.
D. $y=\frac{x+3}{1-x}$.
Chọn B
Dựa vào đồ thị ta có đường tiệm cận đứng $x=-1$ và đường tiệm cận ngang $y=2$ nên chọn phương án B.
Dựa vào đồ thị ta có đường tiệm cận đứng $x=-1$ và đường tiệm cận ngang $y=2$ nên chọn phương án B.
A. $y={{x}^{3}}+3{{x}^{2}}-1$.
B. $y={{x}^{3}}-3{{x}^{2}}-2$.
C. $y=-{{x}^{3}}+3{{x}^{2}}-1$.
D. $y={{x}^{3}}-3{{x}^{2}}+2$.
Chọn D
Dựa vào bảng biến thiên ta có $y\left( 0 \right)=2$ nên chỉ có hàm số $y={{x}^{3}}-3{{x}^{2}}+2$ là thỏa mãn.
Dựa vào bảng biến thiên ta có $y\left( 0 \right)=2$ nên chỉ có hàm số $y={{x}^{3}}-3{{x}^{2}}+2$ là thỏa mãn.
A. $2\sin \alpha -\cos \alpha =\sqrt{3}-1$.
B. $2\cot \alpha +\cos \alpha =0$.
C. $2\sin \alpha +\tan \alpha =0$.
D. $\sin \alpha +\cos \alpha =1+\sqrt{3}$.
Chọn C.
Ta có $cos\alpha =\cos \left( \overrightarrow{u};\overrightarrow{v} \right)=\frac{\overrightarrow{u}.\overrightarrow{v}}{\left| \overrightarrow{u} \right|.\left| \overrightarrow{v} \right|}=\frac{2-6-3}{\sqrt{14}.\sqrt{14}}=-\frac{1}{2}\Rightarrow \alpha ={{120}^{o}}$.
Vậy $2\sin \alpha +\tan \alpha =2.\frac{\sqrt{3}}{2}+\left( -\sqrt{3} \right)=0$.
Ta có $cos\alpha =\cos \left( \overrightarrow{u};\overrightarrow{v} \right)=\frac{\overrightarrow{u}.\overrightarrow{v}}{\left| \overrightarrow{u} \right|.\left| \overrightarrow{v} \right|}=\frac{2-6-3}{\sqrt{14}.\sqrt{14}}=-\frac{1}{2}\Rightarrow \alpha ={{120}^{o}}$.
Vậy $2\sin \alpha +\tan \alpha =2.\frac{\sqrt{3}}{2}+\left( -\sqrt{3} \right)=0$.
| Thời gian (phút) | $[20;25)$ | $[25;30)$ | $[30;35)$ | $[35;40)$ | $[40;45)$ |
| Số ngày | 6 | 6 | 4 | 1 | 1 |
A. $20$.
B. $25$.
C. $15$.
D. $30$.
Chọn B
Khoảng biến thiên của mẫu số liệu ghép nhóm là: $45-20=25$ (phút).
Chọn đáp án B.
Khoảng biến thiên của mẫu số liệu ghép nhóm là: $45-20=25$ (phút).
Chọn đáp án B.
I. $\int\limits_{a}^{b}{f\left( x \right)\text{d}x}=-\int\limits_{b}^{a}{f\left( x \right)\text{d}x}$.
II. $\int\limits_{a}^{b}{2f\left( x \right)\text{d}x}=2\int\limits_{b}^{a}{f\left( x \right)\text{d}x}$.
III. $\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\text{d}x}={{\left[ \int\limits_{a}^{b}{f\left( x \right)\text{d}x} \right]}^{2}}$.
IV. $\int\limits_{a}^{b}{f\left( x \right)\text{d}x}=\int\limits_{a}^{b}{f\left( u \right)\text{d}u}$.
Số mệnh đề đúng trong $4$ mệnh đề trên là:
A. $3$.
B. $4$.
C. $2$.
D. $1$.
Chọn C
Theo định nghĩa và tính chất của tích phân ta có I và IV đúng.
Theo định nghĩa và tính chất của tích phân ta có I và IV đúng.
Tính bán kính $r$ của mặt cầu.
A. $r=2\sqrt[{}]{2}$.
B. $r=\sqrt[{}]{26}$.
C. $r=4$.
D. $r=\sqrt[{}]{2}$.
Chọn A
Mặt cầu $\left( S \right)$ có tâm $I\left( 1\,;\,-1\,;\,2 \right)$ và bán kính $r=\sqrt[{}]{{{1}^{2}}+{{\left( -1 \right)}^{2}}+{{2}^{2}}-\left( -2 \right)}$$=2\sqrt[{}]{2}$.
Mặt cầu $\left( S \right)$ có tâm $I\left( 1\,;\,-1\,;\,2 \right)$ và bán kính $r=\sqrt[{}]{{{1}^{2}}+{{\left( -1 \right)}^{2}}+{{2}^{2}}-\left( -2 \right)}$$=2\sqrt[{}]{2}$.
đây đúng?
A. $d$ song song với đường thẳng $y=3$
B. $d$ song song với đường thẳng $x=3$
C. $d$ có hệ số góc âm
D. $d$ có hệ số góc dương
Chọn A
$y={{x}^{4}}-3{{x}^{2}}+2\Rightarrow y'=4{{x}^{3}}-6x$, $y'=4{{x}^{3}}-6x\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=\pm \frac{\sqrt{6}}{2} \\ \end{align} \right.$.
Vậy điểm cực đại của đồ thị hàm số là: $A\left( 0;2 \right)$.
Tiếp tuyến của đồ thị hàm số $y={{x}^{4}}-3{{x}^{2}}+2$ có hệ số góc: $k=y'\left( 0 \right)=0$.
Vậy phương trình tiếp tuyến $d$ là: $y=2$. Suy ra $d$ song song với đường thẳng $y=3$.
$y={{x}^{4}}-3{{x}^{2}}+2\Rightarrow y'=4{{x}^{3}}-6x$, $y'=4{{x}^{3}}-6x\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=\pm \frac{\sqrt{6}}{2} \\ \end{align} \right.$.
Vậy điểm cực đại của đồ thị hàm số là: $A\left( 0;2 \right)$.
Tiếp tuyến của đồ thị hàm số $y={{x}^{4}}-3{{x}^{2}}+2$ có hệ số góc: $k=y'\left( 0 \right)=0$.
Vậy phương trình tiếp tuyến $d$ là: $y=2$. Suy ra $d$ song song với đường thẳng $y=3$.
A. $\frac{4}{3}$.
B. $\frac{3}{2}$.
C. $\frac{5}{3}$.
D. $\frac{7}{6}$
Chọn A
Ta có: $\int\limits_2^3 {\frac{{3{\rm{x}} + 1}}{{2{{\rm{x}}^2} - x - 1}}d{\rm{x}}} $ $ = \frac{4}{3}\int\limits_2^3 {\frac{1}{{x - 1}}d{\rm{x}}} + \frac{1}{3}\int\limits_2^3 {\frac{1}{{2{\rm{x}} + 1}}d{\rm{x}}} $ $ = \frac{4}{3}\ln \left| {x - 1} \right|\left| \begin{array}{l} 3\\ 2 \end{array} \right. + \frac{1}{6}\ln \left| {2{\rm{x}} + 1} \right|\left| \begin{array}{l} 3\\ 2 \end{array} \right.$
$=\frac{4}{3}\ln 2+\frac{1}{6}\ln 7-\frac{1}{6}\ln 5$.
$P=\frac{4}{3}+\frac{1}{6}-\frac{1}{6}=\frac{4}{3}$
Ta có: $\int\limits_2^3 {\frac{{3{\rm{x}} + 1}}{{2{{\rm{x}}^2} - x - 1}}d{\rm{x}}} $ $ = \frac{4}{3}\int\limits_2^3 {\frac{1}{{x - 1}}d{\rm{x}}} + \frac{1}{3}\int\limits_2^3 {\frac{1}{{2{\rm{x}} + 1}}d{\rm{x}}} $ $ = \frac{4}{3}\ln \left| {x - 1} \right|\left| \begin{array}{l} 3\\ 2 \end{array} \right. + \frac{1}{6}\ln \left| {2{\rm{x}} + 1} \right|\left| \begin{array}{l} 3\\ 2 \end{array} \right.$
$=\frac{4}{3}\ln 2+\frac{1}{6}\ln 7-\frac{1}{6}\ln 5$.
$P=\frac{4}{3}+\frac{1}{6}-\frac{1}{6}=\frac{4}{3}$
PHẦN II. Câu trắc nghiệm đúng sai ( 4 điểm)
Câu 1. Cho hàm số $y=f\left( x \right)=x\ln x$. Các khẳng định sau đúng hay sai?a) $y'=0$ khi $x=-1$.
b) Giá trị lớn nhất của hàm số trên $(0;+\infty )$ bằng 0.
c) Giá trị nhỏ nhất của hàm số trên $(0;+\infty )$ là $-\frac{1}{e}$.
d) Giá trị nhỏ nhất của hàm số $f({{e}^{x}}+{{e}^{-x}})$ bằng $f(2)$
a) Sai
b) Sai
c) Đúng
d) Đúng
Tập xác định của hàm số: $D=\left( 0;+\infty \right)$
Ta có: $y'=\ln x+1$
$y'=0\Leftrightarrow \ln x+1=0\Leftrightarrow \ln x=-1\Leftrightarrow x=\frac{1}{e}$
BBT

a) $y'=0\Leftrightarrow \ln x+1=0\Leftrightarrow \ln x=-1\Leftrightarrow x=\frac{1}{e}$ nên mệnh đề sai.
b) Từ bảng biến thiên ta thấy hàm số không có GTLN trên $(0;+\infty )$ nên mệnh đề sai.
c) Từ bảng biến thiên ta thấy giá trị nhỏ nhất của hàm số trên $(0;+\infty )$ bằng $-\frac{1}{e}$ nên mệnh đề đúng.
d) Ta có: ${{e}^{x}}+{{e}^{-x}}\ge 2\sqrt{{{e}^{x}}.{{e}^{-x}}}\Rightarrow {{e}^{x}}+{{e}^{-x}}\ge 2$. Từ bảng biến thiên ta thấy hàm số luôn đồng biến trên $\left[ 2;+\infty \right)$ nên GTNN của hàm số $f({{e}^{x}}+{{e}^{-x}})$ bằng $f(2)$ nên mệnh đề đúng.
b) Sai
c) Đúng
d) Đúng
Tập xác định của hàm số: $D=\left( 0;+\infty \right)$
Ta có: $y'=\ln x+1$
$y'=0\Leftrightarrow \ln x+1=0\Leftrightarrow \ln x=-1\Leftrightarrow x=\frac{1}{e}$
BBT
a) $y'=0\Leftrightarrow \ln x+1=0\Leftrightarrow \ln x=-1\Leftrightarrow x=\frac{1}{e}$ nên mệnh đề sai.
b) Từ bảng biến thiên ta thấy hàm số không có GTLN trên $(0;+\infty )$ nên mệnh đề sai.
c) Từ bảng biến thiên ta thấy giá trị nhỏ nhất của hàm số trên $(0;+\infty )$ bằng $-\frac{1}{e}$ nên mệnh đề đúng.
d) Ta có: ${{e}^{x}}+{{e}^{-x}}\ge 2\sqrt{{{e}^{x}}.{{e}^{-x}}}\Rightarrow {{e}^{x}}+{{e}^{-x}}\ge 2$. Từ bảng biến thiên ta thấy hàm số luôn đồng biến trên $\left[ 2;+\infty \right)$ nên GTNN của hàm số $f({{e}^{x}}+{{e}^{-x}})$ bằng $f(2)$ nên mệnh đề đúng.
a) Điểm $I(\frac{-1}{2};\frac{1}{2};\frac{-1}{2})$ là trung điểm của đoạn thẳng $AB$.
b) Khi tứ giác $ABC\text{D}$ là hình bình hành thì $O\text{D}=\sqrt{6}$.
c) Điểm $H(\frac{1}{3};\frac{5}{3};\frac{-1}{3})$ là chân đường cao kẻ từ $A$xuống cạnh $BC$ của tam giác $ABC$.
d) Biết điểm $M(x;y;z)$ để biểu thức $3M{{A}^{2}}+2M{{B}^{2}}-M{{C}^{2}}$ đạt giá trị nhỏ nhất, khi đó $4x\,\text{-}\,\text{2y}\,\text{+}\,\text{z}\ =-5$.
Chọn a) Đúng | b) Sai | c) Sai | d) Đúng.
a) Toạ độ trung điểm $I$ của đoạn thẳng $AB$ là $I\left( \frac{0-1}{2};\frac{0+1}{2};\frac{-1+0}{2} \right)\text{ hay I}\left( \frac{-1}{2};\frac{1}{2};\frac{-1}{2} \right).$
Vậy a) đúng.
b) Gọi $D\left( x;\,y;\,z \right)$. Để tứ giác $ABCD$ là hình bình hành thì
$\overrightarrow {AB} = \overrightarrow {DC} $ $ \Rightarrow \left\{ \begin{array}{l} - 1 = 1 - x\\ 1 = 0 - y\\ 1 = 1 - z \end{array} \right.$ $ \Rightarrow D\left( {2;{\mkern 1mu} - 1;{\mkern 1mu} 0} \right) \Rightarrow O{\rm{D}} = \sqrt 5 .$
Vậy b) sai.
c) Ta có $\overrightarrow{BC}=(2;-1;1)$.
Gọi $H(x;y;z)$ là chân đường cao kẻ từ $A$xuống cạnh $BC$ của tam giác $ABC$.
Suy ra $\overrightarrow{BH}=(x+1;y-1;z)$.
Ta có $\left\{ \begin{array}{l} \overrightarrow {BH} //\overrightarrow {BC} \\ \overrightarrow {AH} \bot \overrightarrow {BC} \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} x + 1 = 2t;y - 1 = - t;z = t\,\,\left( 1 \right)\\ \overrightarrow {AH} \cdot \overrightarrow {BC} = 0\,\,\,\,\left( 2 \right) \end{array} \right.$
$\left( 1 \right)\Rightarrow H(2t-1;-t+1;t)$$\Rightarrow \overrightarrow{AH}=(2t-1;-t+1;t+1)$.
$\left( 2 \right)\Rightarrow 2.(2t-1)-(-t+1)+t+1=0$$\Leftrightarrow 6t=2\Leftrightarrow t=\frac{1}{3}\Rightarrow $ $H(\frac{-1}{3};\frac{2}{3};\frac{1}{3})$.
Vậy c) sai.
d)
$M\left( {x;y;z} \right) \Rightarrow \left\{ \begin{array}{l} \overrightarrow {AM} = \left( {x;y;z + 1} \right)\\ \overrightarrow {BM} = \left( {x + 1;y - 1;z} \right)\\ \overrightarrow {CM} = \left( {x - 1;y;z - 1} \right) \end{array} \right.$ $ \Rightarrow \left\{ \begin{array}{l} A{M^2} = {x^2} + {y^2} + {\left( {z + 1} \right)^2}\\ B{M^2} = {\left( {x + 1} \right)^2} + {\left( {y - 1} \right)^2} + {z^2}\\ C{M^2} = {\left( {x - 1} \right)^2} + {y^2} + {\left( {z - 1} \right)^2} \end{array} \right.$ $ \Rightarrow P = 3M{A^2} + 2M{B^2} - M{C^2}$
$=3\left[ {{x}^{2}}+{{y}^{2}}+{{\left( z+1 \right)}^{2}} \right]+2\left[ {{\left( x+1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}+{{z}^{2}} \right]-\left[ {{\left( x-1 \right)}^{2}}+{{y}^{2}}+{{\left( z-1 \right)}^{2}} \right]$
$ = 4{x^2} + 4{y^2} + 4{z^2} + 6x - 4y + 8z + 5$ $ = {\left( {2x + \frac{3}{2}} \right)^2} + {\left( {2y - 1} \right)^2} + {\left( {2z + 2} \right)^2} - \frac{9}{4} \ge - \frac{9}{4}$.
$\Rightarrow MinP=-\frac{9}{4}$ $\Leftrightarrow x=-\frac{3}{4}$, $y=\frac{1}{2}$, $z=-1$, khi đó $M\left( -\frac{3}{4};\frac{1}{2};-1 \right)$.
Vậy $P=4x\,\text{-}\,\text{2y}\,\text{+}\,\text{z}\ \text{=}\,\text{-3}\,\text{-}\,\text{1}\,\text{-}\,\text{1}\,\text{=}\,\text{-}\,\text{5}\text{.}$
Vậy d) đúng.
a) Toạ độ trung điểm $I$ của đoạn thẳng $AB$ là $I\left( \frac{0-1}{2};\frac{0+1}{2};\frac{-1+0}{2} \right)\text{ hay I}\left( \frac{-1}{2};\frac{1}{2};\frac{-1}{2} \right).$
Vậy a) đúng.
b) Gọi $D\left( x;\,y;\,z \right)$. Để tứ giác $ABCD$ là hình bình hành thì
$\overrightarrow {AB} = \overrightarrow {DC} $ $ \Rightarrow \left\{ \begin{array}{l} - 1 = 1 - x\\ 1 = 0 - y\\ 1 = 1 - z \end{array} \right.$ $ \Rightarrow D\left( {2;{\mkern 1mu} - 1;{\mkern 1mu} 0} \right) \Rightarrow O{\rm{D}} = \sqrt 5 .$
Vậy b) sai.
c) Ta có $\overrightarrow{BC}=(2;-1;1)$.
Gọi $H(x;y;z)$ là chân đường cao kẻ từ $A$xuống cạnh $BC$ của tam giác $ABC$.
Suy ra $\overrightarrow{BH}=(x+1;y-1;z)$.
Ta có $\left\{ \begin{array}{l} \overrightarrow {BH} //\overrightarrow {BC} \\ \overrightarrow {AH} \bot \overrightarrow {BC} \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} x + 1 = 2t;y - 1 = - t;z = t\,\,\left( 1 \right)\\ \overrightarrow {AH} \cdot \overrightarrow {BC} = 0\,\,\,\,\left( 2 \right) \end{array} \right.$
$\left( 1 \right)\Rightarrow H(2t-1;-t+1;t)$$\Rightarrow \overrightarrow{AH}=(2t-1;-t+1;t+1)$.
$\left( 2 \right)\Rightarrow 2.(2t-1)-(-t+1)+t+1=0$$\Leftrightarrow 6t=2\Leftrightarrow t=\frac{1}{3}\Rightarrow $ $H(\frac{-1}{3};\frac{2}{3};\frac{1}{3})$.
Vậy c) sai.
d)
$M\left( {x;y;z} \right) \Rightarrow \left\{ \begin{array}{l} \overrightarrow {AM} = \left( {x;y;z + 1} \right)\\ \overrightarrow {BM} = \left( {x + 1;y - 1;z} \right)\\ \overrightarrow {CM} = \left( {x - 1;y;z - 1} \right) \end{array} \right.$ $ \Rightarrow \left\{ \begin{array}{l} A{M^2} = {x^2} + {y^2} + {\left( {z + 1} \right)^2}\\ B{M^2} = {\left( {x + 1} \right)^2} + {\left( {y - 1} \right)^2} + {z^2}\\ C{M^2} = {\left( {x - 1} \right)^2} + {y^2} + {\left( {z - 1} \right)^2} \end{array} \right.$ $ \Rightarrow P = 3M{A^2} + 2M{B^2} - M{C^2}$
$=3\left[ {{x}^{2}}+{{y}^{2}}+{{\left( z+1 \right)}^{2}} \right]+2\left[ {{\left( x+1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}+{{z}^{2}} \right]-\left[ {{\left( x-1 \right)}^{2}}+{{y}^{2}}+{{\left( z-1 \right)}^{2}} \right]$
$ = 4{x^2} + 4{y^2} + 4{z^2} + 6x - 4y + 8z + 5$ $ = {\left( {2x + \frac{3}{2}} \right)^2} + {\left( {2y - 1} \right)^2} + {\left( {2z + 2} \right)^2} - \frac{9}{4} \ge - \frac{9}{4}$.
$\Rightarrow MinP=-\frac{9}{4}$ $\Leftrightarrow x=-\frac{3}{4}$, $y=\frac{1}{2}$, $z=-1$, khi đó $M\left( -\frac{3}{4};\frac{1}{2};-1 \right)$.
Vậy $P=4x\,\text{-}\,\text{2y}\,\text{+}\,\text{z}\ \text{=}\,\text{-3}\,\text{-}\,\text{1}\,\text{-}\,\text{1}\,\text{=}\,\text{-}\,\text{5}\text{.}$
Vậy d) đúng.
a) $f\left( 0 \right)=-1.$
b) $f\left( 1 \right)=2.$
c) $f\left( 2 \right)+f(-2)=-2.$
d) $\int\limits_{0}^{1}{f\left( x \right)\text{d}x}=-\frac{1}{4}.$
Chọn a) Đúng | b) Sai | c) Đúng | d) Đúng.
a) Từ $f\left( x \right)+2xf\left( {{x}^{2}} \right)=2{{x}^{7}}+3{{x}^{3}}-x-1\,\,\,\left( 1 \right)$
Thay $x=0$ vào $\left( 1 \right)$ ta được: $f\left( 0 \right)=-1$
Suy ra mệnh đề a) đúng.
b) Từ $f\left( x \right)+2xf\left( {{x}^{2}} \right)=2{{x}^{7}}+3{{x}^{3}}-x-1\,\,\,$
Thay $x=1$ vào $\left( 1 \right)$ ta được $f\left( 1 \right)+2f\left( 1 \right)=3\Rightarrow f\left( 1 \right)=1\,\,$
Suy ra mệnh đề b) sai.
c) Thay $x=2$ vào $\left( 1 \right)$ ta được: $f\left( 2 \right)+4f\left( 4 \right)=277$
Thay $x=-2$ vào $\left( 1 \right)$ ta được: $f\left( -2 \right)-4f\left( 4 \right)=-279$
Do đó: $f\left( 2 \right)+f\left( -2 \right)=277-279=-2$
Suy ra mệnh đề c) đúng.
d) Từ $\left( 1 \right)$ta có $\int\limits_{0}^{1}{f\left( x \right)\text{d}}x+\int\limits_{0}^{1}{2xf\left( {{x}^{2}} \right)\text{d}}x=\int\limits_{0}^{1}{\left( 2{{x}^{7}}+3{{x}^{3}}-x-1 \right)\,\text{d}}x$
$\Rightarrow \int\limits_{0}^{1}{f\left( x \right)\text{d}}x+\int\limits_{0}^{1}{f\left( {{x}^{2}} \right).{{\left( {{x}^{2}} \right)}^{\prime }}\text{d}}x=-\frac{1}{2}$
Gọi $F(x)$ nguyên hàm của $f\left( x \right)$.
Khi đó $\int\limits_{0}^{1}{f\left( {{x}^{2}} \right).{{\left( {{x}^{2}} \right)}^{\prime }}\text{d}}x=\,\,F\left( {{x}^{2}} \right)\left| \begin{align} & 1 \\ & 0 \\ \end{align} \right.=F(1)-F(0)=\int\limits_{0}^{1}{f\left( x \right)\text{d}}x$
Do đó $\int\limits_0^1 {f\left( x \right){\rm{d}}} x + \int\limits_0^1 {f\left( {{x^2}} \right).{{\left( {{x^2}} \right)}^\prime }{\rm{d}}} x = - \frac{1}{2}$ $ \Rightarrow 2\int\limits_0^1 {f\left( x \right){\rm{d}}} x = - \frac{1}{2}$ $ \Rightarrow \int\limits_0^1 {f\left( x \right){\rm{d}}} x = - \frac{1}{4}\,\,$
Suy ra mệnh đề d) đúng.
a) Từ $f\left( x \right)+2xf\left( {{x}^{2}} \right)=2{{x}^{7}}+3{{x}^{3}}-x-1\,\,\,\left( 1 \right)$
Thay $x=0$ vào $\left( 1 \right)$ ta được: $f\left( 0 \right)=-1$
Suy ra mệnh đề a) đúng.
b) Từ $f\left( x \right)+2xf\left( {{x}^{2}} \right)=2{{x}^{7}}+3{{x}^{3}}-x-1\,\,\,$
Thay $x=1$ vào $\left( 1 \right)$ ta được $f\left( 1 \right)+2f\left( 1 \right)=3\Rightarrow f\left( 1 \right)=1\,\,$
Suy ra mệnh đề b) sai.
c) Thay $x=2$ vào $\left( 1 \right)$ ta được: $f\left( 2 \right)+4f\left( 4 \right)=277$
Thay $x=-2$ vào $\left( 1 \right)$ ta được: $f\left( -2 \right)-4f\left( 4 \right)=-279$
Do đó: $f\left( 2 \right)+f\left( -2 \right)=277-279=-2$
Suy ra mệnh đề c) đúng.
d) Từ $\left( 1 \right)$ta có $\int\limits_{0}^{1}{f\left( x \right)\text{d}}x+\int\limits_{0}^{1}{2xf\left( {{x}^{2}} \right)\text{d}}x=\int\limits_{0}^{1}{\left( 2{{x}^{7}}+3{{x}^{3}}-x-1 \right)\,\text{d}}x$
$\Rightarrow \int\limits_{0}^{1}{f\left( x \right)\text{d}}x+\int\limits_{0}^{1}{f\left( {{x}^{2}} \right).{{\left( {{x}^{2}} \right)}^{\prime }}\text{d}}x=-\frac{1}{2}$
Gọi $F(x)$ nguyên hàm của $f\left( x \right)$.
Khi đó $\int\limits_{0}^{1}{f\left( {{x}^{2}} \right).{{\left( {{x}^{2}} \right)}^{\prime }}\text{d}}x=\,\,F\left( {{x}^{2}} \right)\left| \begin{align} & 1 \\ & 0 \\ \end{align} \right.=F(1)-F(0)=\int\limits_{0}^{1}{f\left( x \right)\text{d}}x$
Do đó $\int\limits_0^1 {f\left( x \right){\rm{d}}} x + \int\limits_0^1 {f\left( {{x^2}} \right).{{\left( {{x^2}} \right)}^\prime }{\rm{d}}} x = - \frac{1}{2}$ $ \Rightarrow 2\int\limits_0^1 {f\left( x \right){\rm{d}}} x = - \frac{1}{2}$ $ \Rightarrow \int\limits_0^1 {f\left( x \right){\rm{d}}} x = - \frac{1}{4}\,\,$
Suy ra mệnh đề d) đúng.
a) Đường thẳng $\Delta $ có vectơ chỉ phương là $\overrightarrow{u}=\left( 1;-2;-3 \right)$
b) Góc giữa đường thẳng $\Delta $ và mặt phẳng $\left( P \right)$ bằng $90{}^\circ $.
c) Đường thẳng ${{d}_{1}}$ là giao tuyến của $\left( P \right)$ và mặt phẳng $\left( Oxy \right)$ Gọi $\alpha $ là góc giữa ${{d}_{1}}$ và mặt phẳng $\left( Oxz \right)$. Khi đó $\alpha >30{}^\circ $.
d) Đường thẳng ${{d}_{2}}$ vuông góc với $\left( P \right)$ và tạo với $\left( Q \right):x+my-3=0$ một góc $30{}^\circ $. Khi đó tổng các giá trị của tham số $m$ bằng $\frac{8}{5}$.
Chọn a) Đúng | b) Sai | c) Sai | d) Sai
a) Đường thẳng Δ có vectơ chỉ phương là \(\vec{u} = (-1;2;3) = - (1;-2;-3)\)
b) Góc giữa đường thẳng Δ và mặt phẳng (P) bằng \(0^\circ\). (P) có VTPT \(\vec{n} = (1;2;-1)\)
Do đó $ \sin(\angle(\Delta, (P))) = \left|\cos(\vec{u}, \vec{n})\right| = \left|\frac{\vec{u} \cdot \vec{n}}{|\vec{u}||\vec{n}|}\right| = \left|\frac{-1 \cdot 1 + 2 \cdot 2 + 3 \cdot (-1)}{\sqrt{14} \cdot \sqrt{6}}\right| = 0 $
Vậy \(\angle(\Delta, (P)) = 0^\circ\)
c) Đường thẳng \(d_1\) là giao tuyến của \((P)\) và mặt phẳng \((Oxy)\). Gọi \(\alpha\) là góc giữa \(d_1\) và mặt phẳng \((Oxz)\). Khi đó \(\alpha > 30^\circ\).
$ (Oxy) \text{ có VTPT là } \vec{k} = (0;0;1), \quad (Oxz) \text{ có VTPT là } \vec{j} = (0;1;0), \quad (P) \text{ có VTPT là } \vec{n} = (1;2;-1) $ $ d = (P) \cap (Oxy) \Rightarrow d \text{ có VTCP là } \vec{u}_d = \left[ \vec{k}, \vec{n} \right] = (-2;1;0) $ $ \sin \beta = \left| \cos(\vec{u}_d, \vec{j}) \right| = \left| \frac{1}{\sqrt{5}} \right| \Rightarrow \beta \approx 27^\circ < 30^\circ $
d) Đường thẳng \(d_2\) vuông góc với \((P)\) và tạo với \((Q): x + my - 3 = 0\) một góc \(30^\circ\). Khi đó tổng các giá trị của tham số \(m\) bằng \(\dfrac{-8}{5}\).
Đường thẳng \(d_2\) vuông góc với \((P)\) nên có VTCP là \(\vec{u}_{d_2} = (1;2;-1)\).
\((Q)\) VTPT là \(\vec{n}_{(Q)} = (1;m;0)\).
$ \sin(d_2, (Q)) = \left| \cos(\vec{n}_Q, \vec{u}_{d_2}) \right| = \left| \frac{1 + 2m}{\sqrt{6} \cdot \sqrt{m^2 + 1}} \right| = \frac{1}{2} $ $ \Leftrightarrow 2|1 + 2m| = \sqrt{6} \cdot \sqrt{m^2 + 1} $ $ \Leftrightarrow 2(1 + 4m + 4m^2) = 3(m^2 + 1) $ $ \Leftrightarrow 5m^2 + 8m - 1 = 0 \Leftrightarrow m = \frac{-4 \pm \sqrt{21}}{5} $
Vậy tổng các giá trị của tham số \(m\) bằng \(\dfrac{-8}{5}\).
a) Đường thẳng Δ có vectơ chỉ phương là \(\vec{u} = (-1;2;3) = - (1;-2;-3)\)
b) Góc giữa đường thẳng Δ và mặt phẳng (P) bằng \(0^\circ\). (P) có VTPT \(\vec{n} = (1;2;-1)\)
Do đó $ \sin(\angle(\Delta, (P))) = \left|\cos(\vec{u}, \vec{n})\right| = \left|\frac{\vec{u} \cdot \vec{n}}{|\vec{u}||\vec{n}|}\right| = \left|\frac{-1 \cdot 1 + 2 \cdot 2 + 3 \cdot (-1)}{\sqrt{14} \cdot \sqrt{6}}\right| = 0 $
Vậy \(\angle(\Delta, (P)) = 0^\circ\)
c) Đường thẳng \(d_1\) là giao tuyến của \((P)\) và mặt phẳng \((Oxy)\). Gọi \(\alpha\) là góc giữa \(d_1\) và mặt phẳng \((Oxz)\). Khi đó \(\alpha > 30^\circ\).
$ (Oxy) \text{ có VTPT là } \vec{k} = (0;0;1), \quad (Oxz) \text{ có VTPT là } \vec{j} = (0;1;0), \quad (P) \text{ có VTPT là } \vec{n} = (1;2;-1) $ $ d = (P) \cap (Oxy) \Rightarrow d \text{ có VTCP là } \vec{u}_d = \left[ \vec{k}, \vec{n} \right] = (-2;1;0) $ $ \sin \beta = \left| \cos(\vec{u}_d, \vec{j}) \right| = \left| \frac{1}{\sqrt{5}} \right| \Rightarrow \beta \approx 27^\circ < 30^\circ $
d) Đường thẳng \(d_2\) vuông góc với \((P)\) và tạo với \((Q): x + my - 3 = 0\) một góc \(30^\circ\). Khi đó tổng các giá trị của tham số \(m\) bằng \(\dfrac{-8}{5}\).
Đường thẳng \(d_2\) vuông góc với \((P)\) nên có VTCP là \(\vec{u}_{d_2} = (1;2;-1)\).
\((Q)\) VTPT là \(\vec{n}_{(Q)} = (1;m;0)\).
$ \sin(d_2, (Q)) = \left| \cos(\vec{n}_Q, \vec{u}_{d_2}) \right| = \left| \frac{1 + 2m}{\sqrt{6} \cdot \sqrt{m^2 + 1}} \right| = \frac{1}{2} $ $ \Leftrightarrow 2|1 + 2m| = \sqrt{6} \cdot \sqrt{m^2 + 1} $ $ \Leftrightarrow 2(1 + 4m + 4m^2) = 3(m^2 + 1) $ $ \Leftrightarrow 5m^2 + 8m - 1 = 0 \Leftrightarrow m = \frac{-4 \pm \sqrt{21}}{5} $
Vậy tổng các giá trị của tham số \(m\) bằng \(\dfrac{-8}{5}\).
PHẦN III. Câu trắc nghiệm trả lời ngắn (3 điểm)
Câu 1. Lúc $12$ giờ, kim giờ và kim phút của một chiếc đồng hồ trùng nhau. Hỏi từ lúc đó đến khi hai kim trùng nhau lần đầu tiên, kim phút quay được một góc lượng giác bao nhiêu radian (làm tròn đến phần hàng chục)?Đáp án: -6,9
Lúc $12$ giờ, hai kim đồng hồ cùng chỉ vào số $12$. Vì kim phút đi nhanh hơn kim giờ nên kim phút đi hết một vòng mà hai kim vẫn chưa gặp nhau.
Hiệu vận tốc của hai kim là: $1-\frac{1}{12}=\frac{11}{12}$( vòng đồng hồ/giờ).
Kể từ lúc $1$ giờ, thời gian để kim phút đuổi kịp kim giờ là: $\frac{1}{12}\div \frac{11}{12}=\frac{1}{11}$( giờ).
Kể từ lúc $12$ giờ, thời gian để hai kim chập nhau lần đầu tiên là: $1+\frac{1}{11}=\frac{12}{11}$( giờ).
Trong $1$ giờ kim phút quay được một vòng$\Rightarrow $ Kim phút quay được $2\pi \left( radian \right)$
Trong $\frac{12}{11}$ giờ kim phút quay được là: $\frac{12}{11}\times 2\pi =\frac{24\pi }{11}\left( radian \right)$.
Do cùng chiều kim đồng hồ là chiều âm$\Rightarrow $ Kim phút quay được là: $-\frac{24\pi }{11}\approx -6,85\left( radian \right)$.
Hiệu vận tốc của hai kim là: $1-\frac{1}{12}=\frac{11}{12}$( vòng đồng hồ/giờ).
Kể từ lúc $1$ giờ, thời gian để kim phút đuổi kịp kim giờ là: $\frac{1}{12}\div \frac{11}{12}=\frac{1}{11}$( giờ).
Kể từ lúc $12$ giờ, thời gian để hai kim chập nhau lần đầu tiên là: $1+\frac{1}{11}=\frac{12}{11}$( giờ).
Trong $1$ giờ kim phút quay được một vòng$\Rightarrow $ Kim phút quay được $2\pi \left( radian \right)$
Trong $\frac{12}{11}$ giờ kim phút quay được là: $\frac{12}{11}\times 2\pi =\frac{24\pi }{11}\left( radian \right)$.
Do cùng chiều kim đồng hồ là chiều âm$\Rightarrow $ Kim phút quay được là: $-\frac{24\pi }{11}\approx -6,85\left( radian \right)$.
Đáp án: 66
Gọi số tiền anh Bình vay là $A$ đồng, với lãi suất $r/$tháng, hàng tháng trả nợ $a$ đồng. Khi đó số tiền còn nợ:
Sau $1$ tháng là ${{T}_{1}}=A(1+r)-a$.
Sau $2$ tháng là ${{T}_{2}}=\left[ A(1+r)-a \right]\left( 1+r \right)-a$$=A{{(1+r)}^{2}}-a\frac{{{\left( 1+r \right)}^{2}}-1}{r}$.
Sau $3$ tháng là ${{T}_{3}}=A{{(1+r)}^{3}}-a\frac{{{\left( 1+r \right)}^{3}}-1}{r}$.
…………………….
Sau $n$ tháng là ${{T}_{n}}=A{{(1+r)}^{n}}-a\frac{{{\left( 1+r \right)}^{n}}-1}{r}$.
Để trả hết nợ thì ${{T}_{n}}=0$$\Leftrightarrow A{{(1+r)}^{n}}-a\frac{{{\left( 1+r \right)}^{n}}-1}{r}=0$
Thay $A=500$,$a=10$,$r=0,85%$ ta có $500{{(1+0,0085)}^{n}}-10\frac{{{\left( 1+0,0085 \right)}^{n}}-1}{0,0085}=0$
$50.{{(1,0085)}^{n}}=\frac{{{\left( 1,0085 \right)}^{n}}-1}{0,0085}$${{(1,0085)}^{n}}=\frac{40}{23}\Leftrightarrow n\approx 65,4$.
Gọi số tiền anh Bình vay là $A$ đồng, với lãi suất $r/$tháng, hàng tháng trả nợ $a$ đồng. Khi đó số tiền còn nợ:
Sau $1$ tháng là ${{T}_{1}}=A(1+r)-a$.
Sau $2$ tháng là ${{T}_{2}}=\left[ A(1+r)-a \right]\left( 1+r \right)-a$$=A{{(1+r)}^{2}}-a\frac{{{\left( 1+r \right)}^{2}}-1}{r}$.
Sau $3$ tháng là ${{T}_{3}}=A{{(1+r)}^{3}}-a\frac{{{\left( 1+r \right)}^{3}}-1}{r}$.
…………………….
Sau $n$ tháng là ${{T}_{n}}=A{{(1+r)}^{n}}-a\frac{{{\left( 1+r \right)}^{n}}-1}{r}$.
Để trả hết nợ thì ${{T}_{n}}=0$$\Leftrightarrow A{{(1+r)}^{n}}-a\frac{{{\left( 1+r \right)}^{n}}-1}{r}=0$
Thay $A=500$,$a=10$,$r=0,85%$ ta có $500{{(1+0,0085)}^{n}}-10\frac{{{\left( 1+0,0085 \right)}^{n}}-1}{0,0085}=0$
$50.{{(1,0085)}^{n}}=\frac{{{\left( 1,0085 \right)}^{n}}-1}{0,0085}$${{(1,0085)}^{n}}=\frac{40}{23}\Leftrightarrow n\approx 65,4$.
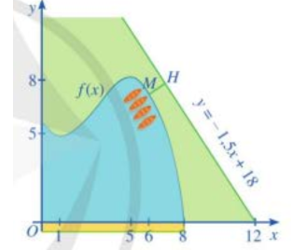
Đơn vị đo độ dài trên mỗi trục tọa độ là 100m. Trong công viên có một con đường chạy dọc theo đồ thị của hàm số $y=-\frac{3}{2}x+18$. Người ta dự định xây dựng bên bờ hồ một bến thuyền đạp nước sao cho khoảng cách từ bến thuyền đến con đường là ngắn nhất . Khi đó tọa độ của điểm để xây bến thuyền là $M\left( a;b \right)$. Tính $T=a-b$.
Đáp án: -1,4

Do $f(x)$ là hàm số liên tục trên $\mathbb{R}$nên điểm M gần đường thẳng $d:y=-\frac{3}{2}x+18$ nhất thì tiếp tuyến của hàm số $y=f\left( x \right)$ tại M song song với d
$ \Rightarrow f'\left( x \right) = - \frac{3}{2}$ $ \Leftrightarrow \frac{1}{{10}}\left( { - 3{x^2} + 18x - 15} \right) = - \frac{3}{2}$ $ \Leftrightarrow - {x^2} + 6x = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = 6 \end{array} \right.$
Khi đó $M\left( 0;\frac{28}{5} \right)$ và $M\left( 6;\frac{37}{5} \right)$
Dựa trên đồ thị ta thấy $M\left( 6;\frac{37}{5} \right)$ là điểm trên đồ thị hàm số $y=f\left( x \right)$ có khoảng cách đến đường thẳng d là nhỏ nhất.
Do đó $a=6,b=\frac{37}{5}\Rightarrow a-b=-1,4$.

Do $f(x)$ là hàm số liên tục trên $\mathbb{R}$nên điểm M gần đường thẳng $d:y=-\frac{3}{2}x+18$ nhất thì tiếp tuyến của hàm số $y=f\left( x \right)$ tại M song song với d
$ \Rightarrow f'\left( x \right) = - \frac{3}{2}$ $ \Leftrightarrow \frac{1}{{10}}\left( { - 3{x^2} + 18x - 15} \right) = - \frac{3}{2}$ $ \Leftrightarrow - {x^2} + 6x = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = 6 \end{array} \right.$
Khi đó $M\left( 0;\frac{28}{5} \right)$ và $M\left( 6;\frac{37}{5} \right)$
Dựa trên đồ thị ta thấy $M\left( 6;\frac{37}{5} \right)$ là điểm trên đồ thị hàm số $y=f\left( x \right)$ có khoảng cách đến đường thẳng d là nhỏ nhất.
Do đó $a=6,b=\frac{37}{5}\Rightarrow a-b=-1,4$.
Đáp án: 108
Gọi đường cong tương ứng với vành trên và vành dưới của máng lần lượt là $\left( {{P}_{1}} \right)$ và $\left( {{P}_{2}} \right)$.
Xét hệ trục tọa độ $Oxy$ như hình vẽ

Khi đó Parabol $\left( {{P}_{1}} \right)$ và $\left( {{P}_{2}} \right)$đều có dạng $y=a{{x}^{2}}+b$.
$\left( {{P}_{1}} \right)$ đi qua các điểm có tọa độ $\left( -1,2;0 \right)$;$\left( 1,2;0 \right)$; $\left( 0;0,5 \right)$.
$\left( {{P}_{2}} \right)$ đi qua các điểm có tọa độ $\left( -1;0 \right)$;$\left( 1;0 \right)$; $\left( 0;0,3 \right)$.
Suy ra $\left( {{P}_{1}} \right):y=-\frac{25}{72}{{x}^{2}}+\frac{1}{2}$ và $\left( {{P}_{2}} \right):y=-\frac{3}{10}{{x}^{2}}+\frac{3}{10}$.
Diện tích mặt cắt của máng Parabol là
$S=2\left[ \int\limits_{0}^{1,2}{\left( -\frac{25}{72}{{x}^{2}}+\frac{1}{2} \right)dx-\int\limits_{0}^{1}{\left( -\frac{3}{10}{{x}^{2}}+\frac{3}{10} \right)dx}} \right]=\frac{2}{5}\left( {{m}^{2}} \right)$.
Vậy thể tích của khối silic làm $90$ mặt máng là $V=90.\frac{2}{5}.3=108\left( {{m}^{3}} \right)$.
Gọi đường cong tương ứng với vành trên và vành dưới của máng lần lượt là $\left( {{P}_{1}} \right)$ và $\left( {{P}_{2}} \right)$.
Xét hệ trục tọa độ $Oxy$ như hình vẽ
Khi đó Parabol $\left( {{P}_{1}} \right)$ và $\left( {{P}_{2}} \right)$đều có dạng $y=a{{x}^{2}}+b$.
$\left( {{P}_{1}} \right)$ đi qua các điểm có tọa độ $\left( -1,2;0 \right)$;$\left( 1,2;0 \right)$; $\left( 0;0,5 \right)$.
$\left( {{P}_{2}} \right)$ đi qua các điểm có tọa độ $\left( -1;0 \right)$;$\left( 1;0 \right)$; $\left( 0;0,3 \right)$.
Suy ra $\left( {{P}_{1}} \right):y=-\frac{25}{72}{{x}^{2}}+\frac{1}{2}$ và $\left( {{P}_{2}} \right):y=-\frac{3}{10}{{x}^{2}}+\frac{3}{10}$.
Diện tích mặt cắt của máng Parabol là
$S=2\left[ \int\limits_{0}^{1,2}{\left( -\frac{25}{72}{{x}^{2}}+\frac{1}{2} \right)dx-\int\limits_{0}^{1}{\left( -\frac{3}{10}{{x}^{2}}+\frac{3}{10} \right)dx}} \right]=\frac{2}{5}\left( {{m}^{2}} \right)$.
Vậy thể tích của khối silic làm $90$ mặt máng là $V=90.\frac{2}{5}.3=108\left( {{m}^{3}} \right)$.
Hỏi trên đường bay của mình, thời gian nhiêu phút thì máy bay, bay qua vùng kiểm soát không lưu? (kết quả làm tròn đến hàng đơn vị)
Đáp án: 50
Ranh giới vùng phủ sóng của đài kiểm soát không lưu là mặt cầu $\left( S \right)$ tâm $O\left( 0;0;0 \right)$ bán kính $R=600\,\text{km}$.
Phương trình mặt cầu $\left( S \right)$ là: ${{x}^{2}}+{{y}^{2}}+{{z}^{2}}={{600}^{2}}$.
Thay phương trình $\left( d \right):\left\{ \begin{align} & x=-1000+100t \\ & y=-200+80t \\ & z=10 \\ \end{align} \right.\left( t\in \mathbb{R} \right)$ vào $\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}={{600}^{2}}$.
Ta được: ${{\left( 100t-1000 \right)}^{2}}+{{\left( 80t-200 \right)}^{2}}+{{10}^{2}}={{600}^{2}}$
$ \Leftrightarrow 16400{t^2} - 232000t + 680100 = 0$ $ \Leftrightarrow \left[ \begin{array}{l} t \approx 10 \Rightarrow B\left( {0;600;10} \right)\\ t \approx 4,15 \Rightarrow C\left( { - 585;132;10} \right) \end{array} \right.$
Khi đó, quãng đường mà máy bay di chuyển qua vùng kiểm soát không lưu là
$S=BC=\sqrt{{{\left( -585 \right)}^{2}}+{{\left( 132-600 \right)}^{2}}}\approx 749$
Thời gian máy bay, bay qua vùng kiểm soát không lưu là:
$t=\frac{749}{900}\approx 0,83\left( \text{h} \right)\approx 50$ (phút)
Ranh giới vùng phủ sóng của đài kiểm soát không lưu là mặt cầu $\left( S \right)$ tâm $O\left( 0;0;0 \right)$ bán kính $R=600\,\text{km}$.
Phương trình mặt cầu $\left( S \right)$ là: ${{x}^{2}}+{{y}^{2}}+{{z}^{2}}={{600}^{2}}$.
Thay phương trình $\left( d \right):\left\{ \begin{align} & x=-1000+100t \\ & y=-200+80t \\ & z=10 \\ \end{align} \right.\left( t\in \mathbb{R} \right)$ vào $\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}={{600}^{2}}$.
Ta được: ${{\left( 100t-1000 \right)}^{2}}+{{\left( 80t-200 \right)}^{2}}+{{10}^{2}}={{600}^{2}}$
$ \Leftrightarrow 16400{t^2} - 232000t + 680100 = 0$ $ \Leftrightarrow \left[ \begin{array}{l} t \approx 10 \Rightarrow B\left( {0;600;10} \right)\\ t \approx 4,15 \Rightarrow C\left( { - 585;132;10} \right) \end{array} \right.$
Khi đó, quãng đường mà máy bay di chuyển qua vùng kiểm soát không lưu là
$S=BC=\sqrt{{{\left( -585 \right)}^{2}}+{{\left( 132-600 \right)}^{2}}}\approx 749$
Thời gian máy bay, bay qua vùng kiểm soát không lưu là:
$t=\frac{749}{900}\approx 0,83\left( \text{h} \right)\approx 50$ (phút)
| viêm phổi | Không viêm phổi | |
| Nghiện thuốc lá | 750 | 1238 |
| Không nghiện thuốc lá | 472 | y |
Đáp án: 5292
Gọi $A$ là biến cố: “Người đó bị viêm phổi”
Gọi $B$ là biến cố: “Người đó không nghiện thuốc lá” $\Rightarrow n\left( B \right)=472+y$
Khi đó $AB$ là biến cố: “Người đó bị viêm phổi và không nghiện thuốc lá”. Vậy $n(AB)=472$.
xác suất để người đó bị viêm phổi trong khi người đó không nghiện thuốc lá là
$P\left( A\backslash B \right)=\frac{P\left( AB \right)}{P\left( B \right)}=\frac{n\left( AB \right)}{n\left( B \right)}=\frac{472}{472+y}\le \frac{1}{7}\Leftrightarrow y\ge 2832$. Vậy nhà nghiên cứu phải tiến hành kiểm tra tối thiểu $750+1238+472+2832=5292$người đàn ông thì xác suất để người đó bị viêm phổi trong khi người đó không nghiện thuốc lá không vượt quá $\frac{1}{7}$.
Gọi $A$ là biến cố: “Người đó bị viêm phổi”
Gọi $B$ là biến cố: “Người đó không nghiện thuốc lá” $\Rightarrow n\left( B \right)=472+y$
Khi đó $AB$ là biến cố: “Người đó bị viêm phổi và không nghiện thuốc lá”. Vậy $n(AB)=472$.
xác suất để người đó bị viêm phổi trong khi người đó không nghiện thuốc lá là
$P\left( A\backslash B \right)=\frac{P\left( AB \right)}{P\left( B \right)}=\frac{n\left( AB \right)}{n\left( B \right)}=\frac{472}{472+y}\le \frac{1}{7}\Leftrightarrow y\ge 2832$. Vậy nhà nghiên cứu phải tiến hành kiểm tra tối thiểu $750+1238+472+2832=5292$người đàn ông thì xác suất để người đó bị viêm phổi trong khi người đó không nghiện thuốc lá không vượt quá $\frac{1}{7}$.
