Đề khảo sát chất lượng Toán 12 thi tốt nghiệp THPT 2025 lần 2 – Trường THPT Khoa học Giáo dục Hà Nội. Có file PDF và đáp án tham khảo.

Câu 1. Khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là $x \ (0 \le x \le 3)$, ta được mặt cắt là một hình vuông có cạnh là $\sqrt{9 - x^2}$ (được mô hình hóa bởi hình vẽ bên dưới). Thể tích của vật thể đó bằng
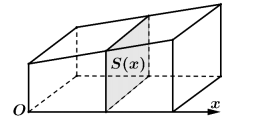
A. $171\pi$.
C. 18.
B. $18\pi$.
D. 171.
Câu 2. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ:
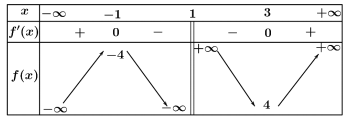
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. $(-\infty;1)$.
C. $(1;3)$.
B. $(-1;3)$.
D. $(1; +\infty)$.
Câu 3. Dũng là học sinh rất giỏi chơi rubik, bạn có thể giải nhiều loại khối rubik khác nhau. Trong một lần luyện tập giải khối rubik $3 \times 3$, bạn Dũng đã tự thống kê lại thời gian giải rubik trong 25 lần giải liên tiếp ở bảng sau:
Khoảng tứ phân vị của mẫu số liệu ghép nhóm (làm tròn đến hàng phần trăm) là
A. 14,38.
C. 10,75.
B. 3,63.
D. 1,75.
Câu 4. Tập nghiệm của bất phương trình $\left(\frac{4}{5}\right)^{2x+1} \le \left(\frac{4}{5}\right)^{2x - 1}$ là
A. $[3; +\infty)$.
C. $[1; +\infty)$.
B. $\mathbb{R}$.
D. $(-\infty;1]$.
Câu 5. Một người gửi tiết kiệm 10 triệu đồng vào một ngân hàng với lãi suất r%/một năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu. Sau 5 năm mỗi rút lãi thì người đó thu được số tiền lãi là
A. 4,026 triệu đồng.
C. 14,026 triệu đồng.
B. 50,7 triệu đồng.
D. 3,5 triệu đồng.
Câu 6. Cho lăng trụ tam giác $ABC.A'B'C'$. Biết diện tích mặt bên $ABA'$ bằng 15 và khoảng cách từ $C$ đến mặt phẳng $(ABA')$ bằng 6 (tham khảo hình vẽ bên cạnh). Thể tích của khối lăng trụ $ABC.A'B'C'$ bằng bao nhiêu?
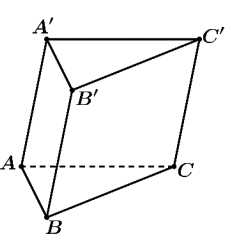
A. 90.
C. 180.
B. 45.
D. 30.
Câu 7. Cho hai biến cố $A, B$ thỏa mãn $\mathbb{P}(\overline{B}) = 0{,}2; \mathbb{P}(A|B) = 0{,}5; \mathbb{P}(A|\overline{B}) = 0{,}3$. Khi đó, $\mathbb{P}(A)$ bằng
A. 0,34.
C. 0,46.
B. 0,31.
D. 0,15.
Câu 8. Cho hàm số $f(x) = e^x + 2x$. Khẳng định nào dưới đây đúng?
A. $\int f(x)dx = e^x + C$.
B. $\int f(x)dx = e^x + 2x^2 + C$.
C. $\int f(x)dx = e^x - x^2 + C$.
D. $\int f(x)dx = e^x + x^2 + C$.
Câu 9. Cho hình lập phương $ABCD.A'B'C'D'$ (tham khảo hình vẽ). Mệnh đề nào sau đây đúng?
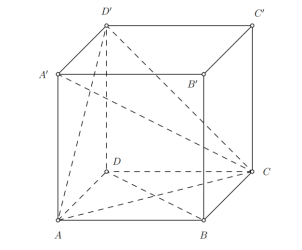
A. $(ADD'A') \perp (ACC'A')$.
B. $(ADD'A') \perp (BCC'D')$.
C. $(ADD'A') \perp (BDD'B')$.
D. $(ADD'A') \perp (ABCD)$.
Câu 10. Cho cấp số cộng $(u_n)$ có $u_1 = -2$ và công sai $d = 3$. Tìm số hạng thứ 10 của cấp số cộng.
A. $u_{10} = 28$.
C. $u_{10} = 25$.
B. $u_{10} = -29$.
D. $u_{10} = -23$.
Câu 11. Trong không gian $Oxyz$, khoảng cách giữa hai mặt phẳng $(P): x + 2y + 2z - 10 = 0$ và $(Q): x + 2y + 2z - 3 = 0$ bằng
A. $\frac{2}{3}$.
C. $\frac{8}{3}$.
B. $\frac{7}{3}$.
D. $\frac{4}{3}$.
Câu 12. Trong không gian $Oxyz$, đường thẳng $d: \begin{cases} x = 1 + 2t \\ y = 3 - t \\ z = 1 - t \end{cases}$ không đi qua điểm nào dưới đây?
A. $P(0;1;2)$.
C. $Q(3;2;0)$.
B. $A(1;3;1)$.
D. $N(5;1;-1)$.
Câu 1. Cho hàm số $y = \frac{ax^2 + bx + c}{mx + n}$ có đồ thị như hình vẽ sau:
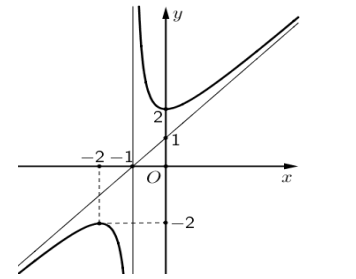
a) Hàm số đã cho nghịch biến trên khoảng $(-2;0)$.
b) Đồ thị của hàm số có tiệm cận xiên y = x + 1.
c) Gọi A, B là hai điểm cực trị của hàm số đã cho, diện tích của tam giác OAB bằng 5 (với O là gốc tọa độ).
d) Một trục đối xứng của đồ thị đã cho là $d : y = (x + 1)\tan\frac{3\pi}{8}$
Câu 2. Một đoàn tàu mang tên TRAM320 đang dừng yên trong sân ga. Đoàn tàu khởi hành từ trạng thái dừng yên với gia tốc $a = 0{,}005t$ (m/s²) biết chiều dài của đoàn tàu là $l = 180$ (m). Sau 50 giây đoàn tàu chuyển sang trạng thái chuyển động đều. Xét tính đúng sai của các khẳng định sau:
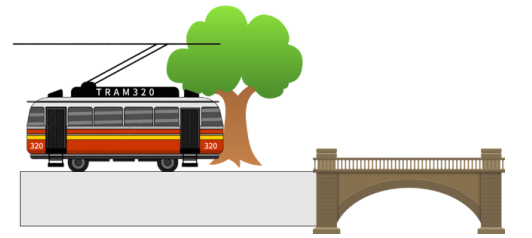
a) Vận tốc của đoàn tàu là $v = 5.10^{-3}t^2$ (m/s).
b) Quãng đường tàu đi được trong 60 giây đầu tiên bằng chiều dài của đoàn tàu.
c) Sau 80 giây, đoàn tàu chuyển động với tốc độ 57,6 (km/h).
d) Sau khi chuyển động đều một thời gian, đoàn tàu gặp một cây cầu có chiều dài 480 (m). Khi đó đoàn tàu đi qua cây cầu đó trong thời gian 30 giây.
Câu 3. Một vòng quay được chia thành 12 phần bằng nhau và được đánh số từ 1 đến 12 như hình vẽ bên dưới:
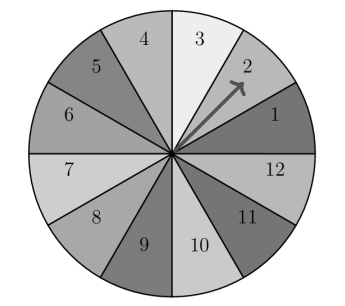
Xét phép thử An và Bình lần lượt quay vòng quay trên.
Gọi A là biến cố “An quay được số chia hết cho 3”, B là biến cố “An quay được số chia hết cho 5”, C là biến cố “Bình quay được số chẵn”. Xét tính đúng sai của các khẳng định sau:
a) Không gian mẫu của phép thử có số kết quả là 24.
b) Số kết quả thuận lợi cho biến cố A, B, C lần lượt là 4, 2, 6.
c) Xác suất để Bình quay được số chẵn, biết An quay được số chia hết cho 3 là $\frac{1}{2}$.
d) Xác suất để An quay được số chia hết cho 5, biết Bình quay được số lẻ là $\frac{1}{12}$.
Câu 4. Trong không gian $Oxyz$, cho đường thẳng $\Delta: \frac{x-2}{-1} = \frac{y-1}{-2} = \frac{z+3}{1}$ và mặt phẳng $(P)$ có phương trình $3x + 6y - 3z + 2025 = 0$. Xét tính đúng sai của các khẳng định sau:
a) Một vectơ chỉ phương của $\Delta$ là $\vec{u} = (-1; -2; 1)$.
b) Một vectơ pháp tuyến của $(P)$ là $\vec{n} = (1; 2; -1)$.
c) Góc giữa $\Delta$ và $(P)$ là $90^\circ$.
d) Lấy tùy ý hai điểm phân biệt $A, B \in \Delta$. Gọi $A', B'$ lần lượt là hình chiếu của $A, B$ lên $(P)$. Khi đó $A'B' = 2025$.
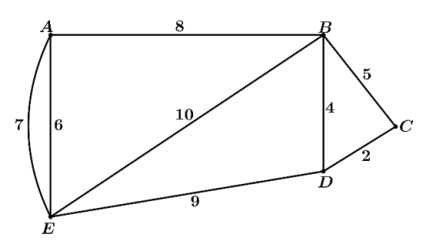
Câu 1. Một người đưa thư xuất phát từ bưu điện ở vị trí A, các điểm cần phát thư nằm dọc theo các con đường cần phải đi qua. Biết người này phải đi trên mỗi con đường ít nhất một lần (để phát được thư cho tất cả các điểm cần phát nằm dọc theo con đường đó) và cuối cùng quay lại điểm xuất phát. Độ dài các con đường như hình vẽ (đơn vị: độ dài). Hỏi tổng quãng đường người đưa thư có thể đi ngắn nhất có thể bằng bao nhiêu?
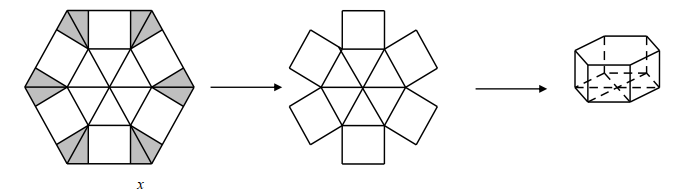
Câu 2. Cho một tấm nhôm hình lục giác đều cạnh 90 cm. Người ta cắt ở mỗi đỉnh của tấm nhôm hai hình tam giác vuông bằng nhau, biết cạnh góc vuông nhỏ bằng x (cm) (cắt phần tô đậm của tấm nhôm) rồi gập tấm nhôm như hình vẽ đã được một hình lăng trụ lục giác đều không có nắp. Tìm x để thể tích của khối lăng trụ lục giác đều trên là lớn nhất (Nếu kết quả là số thập phân thì làm tròn kết quả đến hàng đơn vị)
Câu 3. Một chiếc đồng hồ cát như hình vẽ gồm hai phần đối xứng nhau qua mặt phẳng nằm ngang và đặt trong một hình trụ. Thiết diện thẳng đứng qua trục của nó là hai parabol chung đỉnh và đối xứng nhau qua mặt phẳng nằm ngang. Ban đầu lượng cát dồn hết ở phần trên của đồng hồ thì chiều cao của mực cát bằng $\frac{2}{3}$ chiều cao của bên đó (xem hình vẽ). Cát chảy từ trên xuống dưới với tốc độ $v(t) = 0,2t + 13$ (cm³/phút).
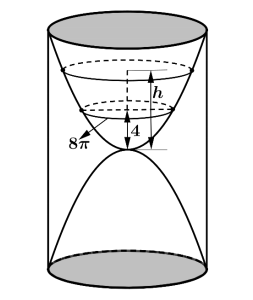
Khi chiều cao của cát còn 4cm thì bề mặt trên cùng của cát tạo thành một đường tròn có chu vi bằng $8\pi$ cm. Biết sau 20 phút thì cát chảy hết xuống phần bên dưới của đồng hồ. Hỏi chiều cao của khối trụ bên ngoài bằng bao nhiêu centimet? (Nếu kết quả là số thập phân thì làm tròn đến hàng đơn vị).
Câu 4. Nhân dịp kỷ niệm 10 năm thành lập trường, các học sinh lựa chọn tham gia thi đấu thể thao hoặc biểu diễn văn nghệ. Lớp 12A1 có 60% số học sinh tham gia thi đấu thể thao và còn lại 40% số học sinh tham gia biểu diễn văn nghệ. Biết rằng các bạn nữ đều tham gia biểu diễn văn nghệ. Trong số các bạn nam có 20% tham gia văn nghệ và 80% tham gia thi đấu thể thao. Chọn ngẫu nhiên 1 học sinh trong lớp 12A1. Biết rằng học sinh này tham gia biểu diễn văn nghệ, xác suất để học sinh này là nữ là bao nhiêu?
(Nếu kết quả là số thập phân thì làm tròn đến hàng phần trăm)
Câu 5. Một bác tài xế thống kê lại độ dài quãng đường (đơn vị: km) mà bác đã lái xe mỗi ngày trong một tháng ở bảng sau:

Hãy xác định độ lệch chuẩn của mẫu số liệu trên? (Nếu kết quả là số thập phân thì làm tròn đến hàng đơn vị)
Câu 6. Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông tại $B$ và có độ dài các cạnh $AB = \sqrt{3},\ BC = 2,\ AA' = \sqrt{2}$. Gọi $M$ là trung điểm của $BC$. Tính khoảng cách giữa hai đường thẳng $AM$ và $B'C$ (Nếu kết quả là số thập phân thì làm tròn đến hàng phần trăm).

PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. (3 ĐIỂM)
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.Câu 1. Khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là $x \ (0 \le x \le 3)$, ta được mặt cắt là một hình vuông có cạnh là $\sqrt{9 - x^2}$ (được mô hình hóa bởi hình vẽ bên dưới). Thể tích của vật thể đó bằng

A. $171\pi$.
C. 18.
B. $18\pi$.
D. 171.
Câu 2. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ:

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. $(-\infty;1)$.
C. $(1;3)$.
B. $(-1;3)$.
D. $(1; +\infty)$.
Câu 3. Dũng là học sinh rất giỏi chơi rubik, bạn có thể giải nhiều loại khối rubik khác nhau. Trong một lần luyện tập giải khối rubik $3 \times 3$, bạn Dũng đã tự thống kê lại thời gian giải rubik trong 25 lần giải liên tiếp ở bảng sau:
| Thời gian giải rubik (giây) | [8;10) | [10;12) | [12;14) | [14;16) | [16;18) |
|---|---|---|---|---|---|
| Số lần | 4 | 6 | 8 | 4 | 3 |
A. 14,38.
C. 10,75.
B. 3,63.
D. 1,75.
Câu 4. Tập nghiệm của bất phương trình $\left(\frac{4}{5}\right)^{2x+1} \le \left(\frac{4}{5}\right)^{2x - 1}$ là
A. $[3; +\infty)$.
C. $[1; +\infty)$.
B. $\mathbb{R}$.
D. $(-\infty;1]$.
Câu 5. Một người gửi tiết kiệm 10 triệu đồng vào một ngân hàng với lãi suất r%/một năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu. Sau 5 năm mỗi rút lãi thì người đó thu được số tiền lãi là
A. 4,026 triệu đồng.
C. 14,026 triệu đồng.
B. 50,7 triệu đồng.
D. 3,5 triệu đồng.
Câu 6. Cho lăng trụ tam giác $ABC.A'B'C'$. Biết diện tích mặt bên $ABA'$ bằng 15 và khoảng cách từ $C$ đến mặt phẳng $(ABA')$ bằng 6 (tham khảo hình vẽ bên cạnh). Thể tích của khối lăng trụ $ABC.A'B'C'$ bằng bao nhiêu?

A. 90.
C. 180.
B. 45.
D. 30.
Câu 7. Cho hai biến cố $A, B$ thỏa mãn $\mathbb{P}(\overline{B}) = 0{,}2; \mathbb{P}(A|B) = 0{,}5; \mathbb{P}(A|\overline{B}) = 0{,}3$. Khi đó, $\mathbb{P}(A)$ bằng
A. 0,34.
C. 0,46.
B. 0,31.
D. 0,15.
Câu 8. Cho hàm số $f(x) = e^x + 2x$. Khẳng định nào dưới đây đúng?
A. $\int f(x)dx = e^x + C$.
B. $\int f(x)dx = e^x + 2x^2 + C$.
C. $\int f(x)dx = e^x - x^2 + C$.
D. $\int f(x)dx = e^x + x^2 + C$.
Câu 9. Cho hình lập phương $ABCD.A'B'C'D'$ (tham khảo hình vẽ). Mệnh đề nào sau đây đúng?

A. $(ADD'A') \perp (ACC'A')$.
B. $(ADD'A') \perp (BCC'D')$.
C. $(ADD'A') \perp (BDD'B')$.
D. $(ADD'A') \perp (ABCD)$.
Câu 10. Cho cấp số cộng $(u_n)$ có $u_1 = -2$ và công sai $d = 3$. Tìm số hạng thứ 10 của cấp số cộng.
A. $u_{10} = 28$.
C. $u_{10} = 25$.
B. $u_{10} = -29$.
D. $u_{10} = -23$.
Câu 11. Trong không gian $Oxyz$, khoảng cách giữa hai mặt phẳng $(P): x + 2y + 2z - 10 = 0$ và $(Q): x + 2y + 2z - 3 = 0$ bằng
A. $\frac{2}{3}$.
C. $\frac{8}{3}$.
B. $\frac{7}{3}$.
D. $\frac{4}{3}$.
Câu 12. Trong không gian $Oxyz$, đường thẳng $d: \begin{cases} x = 1 + 2t \\ y = 3 - t \\ z = 1 - t \end{cases}$ không đi qua điểm nào dưới đây?
A. $P(0;1;2)$.
C. $Q(3;2;0)$.
B. $A(1;3;1)$.
D. $N(5;1;-1)$.
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI. (4 ĐIỂM)
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.Câu 1. Cho hàm số $y = \frac{ax^2 + bx + c}{mx + n}$ có đồ thị như hình vẽ sau:

a) Hàm số đã cho nghịch biến trên khoảng $(-2;0)$.
b) Đồ thị của hàm số có tiệm cận xiên y = x + 1.
c) Gọi A, B là hai điểm cực trị của hàm số đã cho, diện tích của tam giác OAB bằng 5 (với O là gốc tọa độ).
d) Một trục đối xứng của đồ thị đã cho là $d : y = (x + 1)\tan\frac{3\pi}{8}$
Câu 2. Một đoàn tàu mang tên TRAM320 đang dừng yên trong sân ga. Đoàn tàu khởi hành từ trạng thái dừng yên với gia tốc $a = 0{,}005t$ (m/s²) biết chiều dài của đoàn tàu là $l = 180$ (m). Sau 50 giây đoàn tàu chuyển sang trạng thái chuyển động đều. Xét tính đúng sai của các khẳng định sau:

a) Vận tốc của đoàn tàu là $v = 5.10^{-3}t^2$ (m/s).
b) Quãng đường tàu đi được trong 60 giây đầu tiên bằng chiều dài của đoàn tàu.
c) Sau 80 giây, đoàn tàu chuyển động với tốc độ 57,6 (km/h).
d) Sau khi chuyển động đều một thời gian, đoàn tàu gặp một cây cầu có chiều dài 480 (m). Khi đó đoàn tàu đi qua cây cầu đó trong thời gian 30 giây.
Câu 3. Một vòng quay được chia thành 12 phần bằng nhau và được đánh số từ 1 đến 12 như hình vẽ bên dưới:

Xét phép thử An và Bình lần lượt quay vòng quay trên.
Gọi A là biến cố “An quay được số chia hết cho 3”, B là biến cố “An quay được số chia hết cho 5”, C là biến cố “Bình quay được số chẵn”. Xét tính đúng sai của các khẳng định sau:
a) Không gian mẫu của phép thử có số kết quả là 24.
b) Số kết quả thuận lợi cho biến cố A, B, C lần lượt là 4, 2, 6.
c) Xác suất để Bình quay được số chẵn, biết An quay được số chia hết cho 3 là $\frac{1}{2}$.
d) Xác suất để An quay được số chia hết cho 5, biết Bình quay được số lẻ là $\frac{1}{12}$.
Câu 4. Trong không gian $Oxyz$, cho đường thẳng $\Delta: \frac{x-2}{-1} = \frac{y-1}{-2} = \frac{z+3}{1}$ và mặt phẳng $(P)$ có phương trình $3x + 6y - 3z + 2025 = 0$. Xét tính đúng sai của các khẳng định sau:
a) Một vectơ chỉ phương của $\Delta$ là $\vec{u} = (-1; -2; 1)$.
b) Một vectơ pháp tuyến của $(P)$ là $\vec{n} = (1; 2; -1)$.
c) Góc giữa $\Delta$ và $(P)$ là $90^\circ$.
d) Lấy tùy ý hai điểm phân biệt $A, B \in \Delta$. Gọi $A', B'$ lần lượt là hình chiếu của $A, B$ lên $(P)$. Khi đó $A'B' = 2025$.
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN. (3 ĐIỂM)
Thí sinh trả lời từ câu 1 đến câu 6.Câu 1. Một người đưa thư xuất phát từ bưu điện ở vị trí A, các điểm cần phát thư nằm dọc theo các con đường cần phải đi qua. Biết người này phải đi trên mỗi con đường ít nhất một lần (để phát được thư cho tất cả các điểm cần phát nằm dọc theo con đường đó) và cuối cùng quay lại điểm xuất phát. Độ dài các con đường như hình vẽ (đơn vị: độ dài). Hỏi tổng quãng đường người đưa thư có thể đi ngắn nhất có thể bằng bao nhiêu?

Câu 2. Cho một tấm nhôm hình lục giác đều cạnh 90 cm. Người ta cắt ở mỗi đỉnh của tấm nhôm hai hình tam giác vuông bằng nhau, biết cạnh góc vuông nhỏ bằng x (cm) (cắt phần tô đậm của tấm nhôm) rồi gập tấm nhôm như hình vẽ đã được một hình lăng trụ lục giác đều không có nắp. Tìm x để thể tích của khối lăng trụ lục giác đều trên là lớn nhất (Nếu kết quả là số thập phân thì làm tròn kết quả đến hàng đơn vị)

Câu 3. Một chiếc đồng hồ cát như hình vẽ gồm hai phần đối xứng nhau qua mặt phẳng nằm ngang và đặt trong một hình trụ. Thiết diện thẳng đứng qua trục của nó là hai parabol chung đỉnh và đối xứng nhau qua mặt phẳng nằm ngang. Ban đầu lượng cát dồn hết ở phần trên của đồng hồ thì chiều cao của mực cát bằng $\frac{2}{3}$ chiều cao của bên đó (xem hình vẽ). Cát chảy từ trên xuống dưới với tốc độ $v(t) = 0,2t + 13$ (cm³/phút).

Khi chiều cao của cát còn 4cm thì bề mặt trên cùng của cát tạo thành một đường tròn có chu vi bằng $8\pi$ cm. Biết sau 20 phút thì cát chảy hết xuống phần bên dưới của đồng hồ. Hỏi chiều cao của khối trụ bên ngoài bằng bao nhiêu centimet? (Nếu kết quả là số thập phân thì làm tròn đến hàng đơn vị).
Câu 4. Nhân dịp kỷ niệm 10 năm thành lập trường, các học sinh lựa chọn tham gia thi đấu thể thao hoặc biểu diễn văn nghệ. Lớp 12A1 có 60% số học sinh tham gia thi đấu thể thao và còn lại 40% số học sinh tham gia biểu diễn văn nghệ. Biết rằng các bạn nữ đều tham gia biểu diễn văn nghệ. Trong số các bạn nam có 20% tham gia văn nghệ và 80% tham gia thi đấu thể thao. Chọn ngẫu nhiên 1 học sinh trong lớp 12A1. Biết rằng học sinh này tham gia biểu diễn văn nghệ, xác suất để học sinh này là nữ là bao nhiêu?
(Nếu kết quả là số thập phân thì làm tròn đến hàng phần trăm)
Câu 5. Một bác tài xế thống kê lại độ dài quãng đường (đơn vị: km) mà bác đã lái xe mỗi ngày trong một tháng ở bảng sau:

Hãy xác định độ lệch chuẩn của mẫu số liệu trên? (Nếu kết quả là số thập phân thì làm tròn đến hàng đơn vị)
Câu 6. Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông tại $B$ và có độ dài các cạnh $AB = \sqrt{3},\ BC = 2,\ AA' = \sqrt{2}$. Gọi $M$ là trung điểm của $BC$. Tính khoảng cách giữa hai đường thẳng $AM$ và $B'C$ (Nếu kết quả là số thập phân thì làm tròn đến hàng phần trăm).
