Cập nhật đề thi thử tốt nghiệp THPT 2025 môn Toán mới nhất của Sở GD&ĐT Quảng Ninh – bám sát cấu trúc đề thi chính thức, phù hợp định hướng ra đề mới của Bộ Giáo dục. Đề thi có độ phân hóa cao, giúp học sinh lớp 12 luyện tập, đánh giá năng lực, và rèn kỹ năng giải đề hiệu quả. Có đáp án chi tiết kèm theo, hỗ trợ học sinh tự ôn luyện tại nhà. Tài liệu không thể thiếu cho kỳ ôn thi THPT Quốc gia 2025!
Câu 1. Cho cấp số nhân \((u_n)\) có \(u_1 = 12\) và công bội \(q = 2\). Số hạng đầu tiên \(u_1\) bằng:
A. 3.
B. 8.
C. 4.
D. 6.
Câu 2. Họ nguyên hàm của hàm số \(f(x) = \sin x\) là:
A. \(\int f(x)\,dx = -\cos x + C.\)
B. \(\int f(x)\,dx = \tan x + C.\)
C. \(\int f(x)\,dx = \cos x + C.\)
D. \(\int f(x)\,dx = \cot x + C.\)
Câu 3. Cho hàm số \(y = 2x - 1 - \dfrac{3}{x+2}\). Đường tiệm cận xiên của đồ thị hàm số đã cho là:
A. \(y = 2x + 1.\)
B. \(y = 2x + 1.\)
C. \(y = -2x - 1.\)
D. \(y = 2x - 1.\)
Câu 4. Khảo sát thời gian tự học bài ở nhà của học sinh khối 12 ở trường X, ta thu được bảng sau:
Phương sai của mẫu số liệu ghép nhóm (làm tròn kết quả đến hàng đơn vị) là:
A. $874$.
B. $873$.
C. $875$.
D. $872$.
Câu 5. Cho tứ diện \(ABCD\), hai điểm \(M, N\) theo thứ tự là trung điểm của \(AB, CD\). Điểm \(G\) trung điểm đoạn thẳng \(MN\) (tham khảo hình vẽ bên).
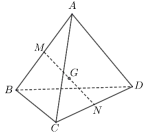
Phát biểu nào sau đây sai?
A. \(\overrightarrow{AD} + \overrightarrow{BC} = \overrightarrow{AC} + \overrightarrow{BD}.\)
B. \(\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} + \overrightarrow{GD} = \vec{0}.\)
C. \(\overrightarrow{AD} + \overrightarrow{BC} = \overrightarrow{AC} + \overrightarrow{DB}.\)
D. \(\overrightarrow{AD} + \overrightarrow{BC} = 2\overrightarrow{MN}.\)
Câu 6. Tập nghiệm của bất phương trình \(\log_{0.5}(x - 7) + 2 > 0\) là:
A. \((7; 11)\)
B. \([7; 11]\)
C. \((11; +\infty)\)
D. \((-\infty; 11)\)
Điều kiện: $x-7>0\Leftrightarrow x>7$.
Khi đó: ${{\log }_{0,5}}\left( x-7 \right)+2>0\Leftrightarrow {{\log }_{0,5}}\left( x-7 \right)>-2$ $\Leftrightarrow x-7<{{\left( 0,5 \right)}^{-2}}\Leftrightarrow x-7<4\Leftrightarrow x<11$.
Kết hợp điều kiện $x>7$ ta được tập nghiệm của bất phương trình là $S=\left( 7;11 \right)$.
Câu 7. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B\), \(AD = 2AB = 2BC\), đường thẳng \(SA\) vuông góc với mặt phẳng đáy (tham khảo hình vẽ bên).
Mặt phẳng nào sau đây vuông góc với mặt phẳng \((SCD)\)?
A. \((SAB)\)
B. \((SBD)\)
C. \((SAD)\)
D. \((SAC)\)
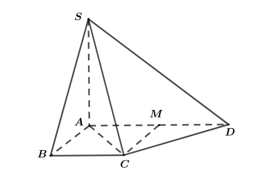
Gọi $M$ là trung điểm của $AD$. Do $ABCD$ là hình thang vuông tại $A$ và $B$, $AD=2AB=2BC$ nên $ABCM$ là hình vuông, từ đó suy ra $AM=MD=MC$, khi đó tam giác $ACD$ vuông tại $C$.
Ta có $SA\bot \left( ABCD \right)\Rightarrow SA\bot CD$, mà $CD\bot AC$ nên $CD\bot \left( SAC \right)$ với $CD\subset \left( SCD \right)$ từ đó ta có $\left( SCD \right)\bot \left( SAC \right)$. Chọn D
Câu 8. Phương trình \(\sin\left(x - \dfrac{\pi}{3}\right) = -1\) có các nghiệm là:
A. \(x = \dfrac{2\pi}{3} + k2\pi \ (k \in \mathbb{Z})\)
B. \(x = -\dfrac{\pi}{6} + k2\pi \ (k \in \mathbb{Z})\)
C. \(x = \dfrac{\pi}{6} + k\pi \ (k \in \mathbb{Z})\)
D. \(x = \dfrac{7\pi}{6} + k2\pi \ (k \in \mathbb{Z})\)
Câu 9. Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(d\) có phương trình $ \frac{x - 1}{3} = \frac{y + 2}{-4} = \frac{z}{-2} $ Vectơ nào sau đây là một vectơ chỉ phương của đường thẳng \(d\)?
A. \(\vec{u}_1 = (3; 4; 2)\)
B. \(\vec{u}_2 = (3; -4; -2)\)
C. \(\vec{u}_3 = (6; 8; 4)\)
D. \(\vec{u}_4 = (-9; 12; -6)\)
Câu 10. Trong không gian với hệ tọa độ \(Oxyz\), cho điểm \(M(2; -3; 1)\) và mặt phẳng \((P): 2x - 2y + z + 3 = 0\). Mặt phẳng đi qua điểm \(M\) và song song với mặt phẳng \((P)\) có phương trình là:
A. \(2x - 2y + z + 11 = 0\)
B. \(2x - 2y + z + 1 = 0\)
C. \(2x - 2y + z - 11 = 0\)
D. \(-2x - 2y + z - 11 = 0\)
Câu 11. Cho hàm số \(y = \dfrac{ax + b}{cx + d}\) (với \(c \ne 0, ad - bc \ne 0\)) có đồ thị như hình vẽ bên.
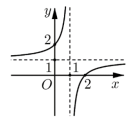
Khẳng định nào sau đây đúng?
A. \(\lim\limits_{x \to +\infty} f(x) = +\infty\) và \(\lim\limits_{x \to -\infty} f(x) = -\infty\)
B. \(\lim\limits_{x \to -\infty} f(x) = +\infty\) và \(\lim\limits_{x \to +\infty} f(x) = -\infty\)
C. Đồ thị hàm số có hai điểm cực trị.
D. Hàm số đồng biến trên khoảng \((-\infty; +\infty)\)
Câu 12. Cho hai hàm số \(y = f(x), y = g(x)\) liên tục trên đoạn \([a; b]\). Xét hình phẳng \(H\) giới hạn bởi các đồ thị \(y = f(x), y = g(x)\) và hai đường thẳng \(x = a, x = b\). Diện tích hình phẳng \(H\) là:
A. \(\int_a^b \left[f(x) - g(x)\right] \, dx\)
B. \(\int_a^b \left[g(x) - f(x)\right] \, dx\)
C. \(\int_a^b \left[f(x) - g(x)\right]^2 \, dx\)
D. \(\int_a^b \left|f(x) - g(x)\right| \, dx\)
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S).
Câu 1. Một tên lửa phóng thẳng đứng từ mặt đất với vận tốc ban đầu \(v_0 = 50\text{ m/s}\). Gia tốc của tên lửa (do lực đẩy và trọng lực) phụ thuộc vào thời gian theo công thức \(a(t) = 10 - 2t\) (m/s²). Sau thời gian 10s, tên lửa hết nhiên liệu và tiếp tục bay với gia tốc \(a = -9{,}8\text{ m/s}^2\).
a) Vận tốc của tên lửa đạt được tại thời điểm \(t = 10s\) là 50 m/s.
b) Độ cao của tên lửa đạt tại thời điểm \(t = 10s\) là 660 m.
c) Tên lửa đạt độ cao lớn nhất tại thời điểm \(t = 15s\) (làm tròn kết quả đến hàng đơn vị).
d) Độ cao lớn nhất tên lửa đạt được (làm tròn kết quả đến hàng đơn vị) là 766 m.
Câu 2. Một tàu thăm dò tự hành (AUV) đang hoạt động dưới biển sâu. Hệ tọa độ \(Oxyz\) được thiết lập với mặt nước biển yên tĩnh là mặt phẳng \((Oxy)\), trục \(Oz\) hướng thẳng đứng xuống dưới (độ sâu \(s > 0\)), đơn vị tính bằng hectomét (hm). AUV bắt đầu hành trình từ vị trí \(A(8; 6; 1)\) và dự định di chuyển theo đường thẳng đến vị trí cuối \(B(-4; 2; 2)\). Trong hành trình của mình AUV cần tránh một khu vực hình cầu \((S)\), tâm tại điểm \(K=(-2; 4; -2)\), bán kính \(R = 1\) hm (khu vực có thiết bị nhạy cảm).
a) Đường thẳng chứa hành trình của AUV có phương trình \(\dfrac{x - 8}{-4} = \dfrac{y - 6}{-8} = \dfrac{z - 1}{1}\)
b) Mặt cầu (S) có phương trình \((x + 2)^2 + (y - 4)^2 + (z + 2)^2 = 1\)
c) Trên hành trình AUV luôn cách tâm \(K\) một khoảng lớn hơn bán kính \(R\)
d) Hành trình của AUV không đi qua khu vực có thiết bị nhạy cảm hình cầu (S)
Câu 3. Một hệ thống AI được sử dụng để kiểm tra đạo văn trong các bài viết học sinh nộp. Theo thống kê: có 1% bài viết là đạo văn, 99% bài viết là chính chủ (không đạo văn). Phần mềm kiểm tra có độ chính xác như sau: Nếu bài viết là đạo văn, phần mềm phát hiện đúng với xác suất 98%; Nếu bài viết là chính chủ, phần mềm cảnh báo nhầm là đạo văn với xác suất 3%. Kiểm tra ngẫu nhiên một bài viết của học sinh nộp.
Gọi \(A\) là biến cố “Bài viết thực sự là đạo văn”.
Gọi \(B\) là biến cố “Phần mềm cảnh báo bài viết là đạo văn”.
- Xác suất \(P(B) = 0{,}039\).
- b) Xác suất \(P(A) = 0{,}01\) và \(P(\bar{A}) = 0{,}99\).
- c) Xác suất có điều kiện \(P(A|B) = 0{,}7\).
- d) Trong số những bài viết bị phần mềm cảnh báo là đạo văn, có nhiều khả năng là bài viết chính chủ hơn là đạo văn.

Câu 4. Cho hàm số \( y = x - 1 + \dfrac{9}{x+2} \)
a) Tập xác định của hàm số là \( \mathbb{R} \setminus \{-2\} \).
b) Hàm số có đạo hàm là \( y' = 1 - \dfrac{9}{(x+2)^2}, \forall x \ne -2 \).
c) Hàm số đồng biến trên các khoảng \( (-\infty; -5) \) và \( (1; +\infty) \).
d) Hàm số có giá trị cực đại lớn hơn giá trị cực tiểu.
Câu 1. Tại một khu trung tâm dữ liệu, kỹ sư IT cần kiểm tra kết nối giữa các máy chủ trong hệ thống gồm các trạm \( A, B, C, D, E \). Các tuyến cáp quang nối giữa các trạm được biểu diễn trong sơ đồ sau, với con số ghi trên mỗi tuyến là chiều dài dây cáp (đơn vị: km).
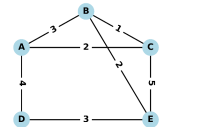
Kỹ sư cần thực hiện một hành trình bắt đầu từ một trạm bất kỳ, đi qua tất cả các tuyến cáp ít nhất một lần và kết thúc tại đúng trạm khởi hành, nhằm đảm bảo toàn bộ hệ thống được kiểm tra. Tổng chiều dài đường đi ngắn nhất mà kỹ sư cần di chuyển là bao nhiêu km?
Câu 2. Một công ty đang triển khai chiến dịch quảng cáo sản phẩm mới. Số tiền đầu tư quảng cáo là \( A \) (triệu đồng). Theo kết quả nghiên cứu thị trường, số lượng sản phẩm bán ra (đơn vị: sản phẩm) phụ thuộc vào chi phí quảng cáo theo hàm: $ q(A) = 1000 + \frac{1013}{5} \ln(1 + A) $ Biết rằng, chi phí sản xuất mỗi sản phẩm là 10 triệu đồng và giá bán mỗi sản phẩm là 20 triệu đồng. Giá trị lợi nhuận tối đa mà công ty có thể đạt được là bao nhiêu tỉ đồng (làm tròn kết quả đến hàng phần mười)?
Câu 3. Một người tham gia trò chơi với 3 hộp quà đặc biệt: Hộp màu vàng có 2 điện thoại iPhone và 3 tai nghe, hộp màu bạc có 4 điện thoại iPhone và 1 tai nghe và hộp màu đồng có 3 điện thoại iPhone và 2 tai nghe. Luật chơi được thực hiện qua hai bước sau:
Bước 1. Người chơi chọn ngẫu nhiên 1 hộp.
Bước 2. Từ hộp đã chọn, người chơi lấy ngẫu nhiên 1 món quà:
- Nếu quà là điện thoại iPhone, người chơi giữ nó và lấy thêm 1 quà nữa từ cùng hộp.
- Nếu quà là tai nghe, trò chơi kết thúc.
Biết rằng người chơi lấy được 2 điện thoại iPhone, tính xác suất để người đó lấy từ hộp màu bạc (làm tròn kết quả đến hàng phần mười).
Câu 4. Trong một trung tâm nghiên cứu robot bay, người ta bố trí một thiết bị định vị tại điểm cố định \( A(1;0;2) \) trong không gian ba chiều với hệ tọa độ \( Oxyz \) (các đơn vị tọa độ được tính bằng mét). Thiết bị này giao tiếp đồng thời với hai cảm biến: Cảm biến thứ nhất di chuyển dọc theo đường thẳng $ \Delta: \frac{x - 3}{1} = \frac{y + 1}{2} = \frac{z - 4}{-1} $ , cảm biến thứ hai được gắn trên mặt phẳng \( (\alpha): 2x - y + z + 1 = 0 \). Giữa hai cảm biến được kết nối bởi một đường truyền \( BC \), trong đó \( B \) nằm trên đường thẳng \( \Delta \), \( C \) nằm trên mặt phẳng \( (\alpha) \) và thiết bị định vị tại \( A \) là trung điểm của đoạn \( BC \). Biết rằng đường thẳng \( BC \) có một vectơ chỉ phương \( \vec{u} = (-2; a; b) \), hãy tính giá trị \( a + 2b \).
Câu 5. Cho một hộp quà hình lập phương có cạnh bằng 10 cm. Trong hộp có một quả cầu pha lê lớn đặc được đặt vừa khít vào hộp sao cho quả cầu tiếp xúc với tất cả các mặt của hộp. Ở 8 góc của hình lập phương, có 8 quả cầu pha lê nhỏ cũng tiếp xúc với các mặt hộp và tiếp xúc với quả cầu lớn. Để epoxy resin (một loại keo tổng hợp trong suốt dùng trong thi công mỹ nghệ) vào đầy hộp để trang trí. Tính thể tích phần keo cần đổ, theo đơn vị lít (làm tròn kết quả đến hàng phần mười).
Câu 6. Một công ty đang thiết kế một bảng quảng cáo hình chữ nhật \(ABCD\) có kích thước \(AB = 12\,m\) và \(AD = 8\,m\). Phần trung tâm của bảng sẽ được in nội dung quảng cáo, được mô tả là phần tô đậm (xem hình minh họa).
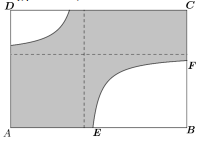
Hai đường cong trong hình là một phần của đồ thị hàm số có dạng \( y = \frac{ax + b}{cx + d} \), đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số này đều cách điểm \(A\) một khoảng bằng 5 m. Đồ thị giao với cạnh \(AB\) tại điểm \(E\) thỏa mãn \( \frac{AE}{AB} = \frac{7}{15} \). Diện tích phần in nội dung quảng cáo là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)?
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.Câu 1. Cho cấp số nhân \((u_n)\) có \(u_1 = 12\) và công bội \(q = 2\). Số hạng đầu tiên \(u_1\) bằng:
A. 3.
B. 8.
C. 4.
D. 6.
Chọn A
Ta có ${{u}_{3}}={{u}_{1}}.{{q}^{2}}$ nên ${{u}_{1}}=\frac{{{u}_{3}}}{{{q}^{2}}}=\frac{12}{{{2}^{2}}}=3$.
Ta có ${{u}_{3}}={{u}_{1}}.{{q}^{2}}$ nên ${{u}_{1}}=\frac{{{u}_{3}}}{{{q}^{2}}}=\frac{12}{{{2}^{2}}}=3$.
A. \(\int f(x)\,dx = -\cos x + C.\)
B. \(\int f(x)\,dx = \tan x + C.\)
C. \(\int f(x)\,dx = \cos x + C.\)
D. \(\int f(x)\,dx = \cot x + C.\)
Chọn A \[\int{f(x)dx=-\cos x+C}\]
A. \(y = 2x + 1.\)
B. \(y = 2x + 1.\)
C. \(y = -2x - 1.\)
D. \(y = 2x - 1.\)
Ta có: $\underset{x\to +\infty }{\mathop{\lim \,}}\,\left[ y-\left( 2x-1 \right) \right]=\underset{x\to +\infty }{\mathop{\lim \,}}\,\left( -\frac{3}{x+2} \right)=0$, tương tự $\underset{x\to -\infty }{\mathop{\lim \,}}\,\left[ y-\left( 2x-1 \right) \right]=\underset{x\to -\infty }{\mathop{\lim \,}}\,\left( -\frac{3}{x+2} \right)=0$
Do đó đường thẳng $y=2x-1$ là đường tiệm cận xiên của đồ thị hàm số đã cho.
Do đó đường thẳng $y=2x-1$ là đường tiệm cận xiên của đồ thị hàm số đã cho.
| Thời gian (phút) | (0; 30) | (30; 60) | (60; 90) | (90; 120) | (120; 150) |
|---|---|---|---|---|---|
| Số học sinh | 75 | 125 | 250 | 82 | 18 |
A. $874$.
B. $873$.
C. $875$.
D. $872$.
Gọi ${{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}},{{x}_{5}}$ lần lượt là giá trị đại diện của các nhóm đã cho.
Ta có: ${{x}_{1}}=15,{{x}_{2}}=45,{{x}_{3}}=75,{{x}_{4}}=105,{{x}_{5}}=135.$
Số trung bình cộng của mẫu số liệu là: $\overline{x}=\frac{15.75+45.125+75.250+105.82+135.18}{550}=\frac{3654}{55}$
Phương sai của mẫu số liệu là:
${{s}^{2}}=\frac{75.{{\left( 15-\overline{x} \right)}^{2}}+125.{{\left( 45-\overline{x} \right)}^{2}}+250.{{\left( 75-\overline{x} \right)}^{2}}+82.{{\left( 105-\overline{x} \right)}^{2}}+18.{{\left( 135-\overline{x} \right)}^{2}}}{550}\approx 874$
Ta có: ${{x}_{1}}=15,{{x}_{2}}=45,{{x}_{3}}=75,{{x}_{4}}=105,{{x}_{5}}=135.$
Số trung bình cộng của mẫu số liệu là: $\overline{x}=\frac{15.75+45.125+75.250+105.82+135.18}{550}=\frac{3654}{55}$
Phương sai của mẫu số liệu là:
${{s}^{2}}=\frac{75.{{\left( 15-\overline{x} \right)}^{2}}+125.{{\left( 45-\overline{x} \right)}^{2}}+250.{{\left( 75-\overline{x} \right)}^{2}}+82.{{\left( 105-\overline{x} \right)}^{2}}+18.{{\left( 135-\overline{x} \right)}^{2}}}{550}\approx 874$

Phát biểu nào sau đây sai?
A. \(\overrightarrow{AD} + \overrightarrow{BC} = \overrightarrow{AC} + \overrightarrow{BD}.\)
B. \(\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} + \overrightarrow{GD} = \vec{0}.\)
C. \(\overrightarrow{AD} + \overrightarrow{BC} = \overrightarrow{AC} + \overrightarrow{DB}.\)
D. \(\overrightarrow{AD} + \overrightarrow{BC} = 2\overrightarrow{MN}.\)
Ta có $\overrightarrow{AD}+\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{DB}$ $ \Leftrightarrow \overrightarrow {AD} - \overrightarrow {AC} + \overrightarrow {BC} = \overrightarrow {DB} $
$\Leftrightarrow \overrightarrow{CD}+\overrightarrow{BC}=\overrightarrow{DB}$ $\Leftrightarrow \overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{DB}$ $\Leftrightarrow \overrightarrow{BD}=\overrightarrow{DB}$ (vô lí).
Nên C sai.
$\Leftrightarrow \overrightarrow{CD}+\overrightarrow{BC}=\overrightarrow{DB}$ $\Leftrightarrow \overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{DB}$ $\Leftrightarrow \overrightarrow{BD}=\overrightarrow{DB}$ (vô lí).
Nên C sai.
A. \((7; 11)\)
B. \([7; 11]\)
C. \((11; +\infty)\)
D. \((-\infty; 11)\)
Điều kiện: $x-7>0\Leftrightarrow x>7$.
Khi đó: ${{\log }_{0,5}}\left( x-7 \right)+2>0\Leftrightarrow {{\log }_{0,5}}\left( x-7 \right)>-2$ $\Leftrightarrow x-7<{{\left( 0,5 \right)}^{-2}}\Leftrightarrow x-7<4\Leftrightarrow x<11$.
Kết hợp điều kiện $x>7$ ta được tập nghiệm của bất phương trình là $S=\left( 7;11 \right)$.
Câu 7. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B\), \(AD = 2AB = 2BC\), đường thẳng \(SA\) vuông góc với mặt phẳng đáy (tham khảo hình vẽ bên).
Mặt phẳng nào sau đây vuông góc với mặt phẳng \((SCD)\)?
A. \((SAB)\)
B. \((SBD)\)
C. \((SAD)\)
D. \((SAC)\)

Gọi $M$ là trung điểm của $AD$. Do $ABCD$ là hình thang vuông tại $A$ và $B$, $AD=2AB=2BC$ nên $ABCM$ là hình vuông, từ đó suy ra $AM=MD=MC$, khi đó tam giác $ACD$ vuông tại $C$.
Ta có $SA\bot \left( ABCD \right)\Rightarrow SA\bot CD$, mà $CD\bot AC$ nên $CD\bot \left( SAC \right)$ với $CD\subset \left( SCD \right)$ từ đó ta có $\left( SCD \right)\bot \left( SAC \right)$. Chọn D
A. \(x = \dfrac{2\pi}{3} + k2\pi \ (k \in \mathbb{Z})\)
B. \(x = -\dfrac{\pi}{6} + k2\pi \ (k \in \mathbb{Z})\)
C. \(x = \dfrac{\pi}{6} + k\pi \ (k \in \mathbb{Z})\)
D. \(x = \dfrac{7\pi}{6} + k2\pi \ (k \in \mathbb{Z})\)
Ta có
$\begin{align}
& \sin \left( x-\frac{\pi }{3} \right)=-1 \\
& \Leftrightarrow x-\frac{\pi }{3}=-\frac{\pi }{2}+2k\pi \\
& \Leftrightarrow x=-\frac{\pi }{6}+2k\pi (k\in \mathbb{Z}). \\
\end{align}$
Chọn B
$\begin{align}
& \sin \left( x-\frac{\pi }{3} \right)=-1 \\
& \Leftrightarrow x-\frac{\pi }{3}=-\frac{\pi }{2}+2k\pi \\
& \Leftrightarrow x=-\frac{\pi }{6}+2k\pi (k\in \mathbb{Z}). \\
\end{align}$
Chọn B
A. \(\vec{u}_1 = (3; 4; 2)\)
B. \(\vec{u}_2 = (3; -4; -2)\)
C. \(\vec{u}_3 = (6; 8; 4)\)
D. \(\vec{u}_4 = (-9; 12; -6)\)
Véctơ chỉ phương $\overrightarrow{u_1}=(-9 ; 12 ;-6)$
A. \(2x - 2y + z + 11 = 0\)
B. \(2x - 2y + z + 1 = 0\)
C. \(2x - 2y + z - 11 = 0\)
D. \(-2x - 2y + z - 11 = 0\)
Gọi $\left( Q \right)$ đi qua điểm $M$ và song song với mặt phẳng $(P)$
$\Rightarrow \left( Q \right):2x-2y+z+m=0\,\left( m\ne 3 \right)$
Thay $M(2 ;-3 ; 1)$ vào $\left( Q \right)$ ta được: $m=-11$ (nhận)
$\Rightarrow \left( Q \right):2x-2y+z-11=0.$
$\Rightarrow \left( Q \right):2x-2y+z+m=0\,\left( m\ne 3 \right)$
Thay $M(2 ;-3 ; 1)$ vào $\left( Q \right)$ ta được: $m=-11$ (nhận)
$\Rightarrow \left( Q \right):2x-2y+z-11=0.$

Khẳng định nào sau đây đúng?
A. \(\lim\limits_{x \to +\infty} f(x) = +\infty\) và \(\lim\limits_{x \to -\infty} f(x) = -\infty\)
B. \(\lim\limits_{x \to -\infty} f(x) = +\infty\) và \(\lim\limits_{x \to +\infty} f(x) = -\infty\)
C. Đồ thị hàm số có hai điểm cực trị.
D. Hàm số đồng biến trên khoảng \((-\infty; +\infty)\)
Dựa vào đồ thị hàm số đã cho ta nhận thấy:
Thứ nhất: $\underset{x\to -\infty }{\mathop{\lim }}\,f\left( x \right)=1$ và $\underset{x\to +\infty }{\mathop{\lim }}\,f\left( x \right)=1$.
Thứ hai: $\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,f\left( x \right)=-\infty $ và $\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,f\left( x \right)=+\infty $.
Thứ ba: Đồ thị hàm số không có điểm cực trị.
Thứ tư: Hàm số đồng biến trên các khoảng $\left( -\infty ;1 \right)$ và $\left( 1;\infty \right)$.
Vậy khẳng định đúng là $\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,f\left( x \right)=-\infty $ và $\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,f\left( x \right)=+\infty $.
Thứ nhất: $\underset{x\to -\infty }{\mathop{\lim }}\,f\left( x \right)=1$ và $\underset{x\to +\infty }{\mathop{\lim }}\,f\left( x \right)=1$.
Thứ hai: $\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,f\left( x \right)=-\infty $ và $\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,f\left( x \right)=+\infty $.
Thứ ba: Đồ thị hàm số không có điểm cực trị.
Thứ tư: Hàm số đồng biến trên các khoảng $\left( -\infty ;1 \right)$ và $\left( 1;\infty \right)$.
Vậy khẳng định đúng là $\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,f\left( x \right)=-\infty $ và $\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,f\left( x \right)=+\infty $.
A. \(\int_a^b \left[f(x) - g(x)\right] \, dx\)
B. \(\int_a^b \left[g(x) - f(x)\right] \, dx\)
C. \(\int_a^b \left[f(x) - g(x)\right]^2 \, dx\)
D. \(\int_a^b \left|f(x) - g(x)\right| \, dx\)
Xét hình phẳng $\left( H \right)$ giới hạn bởi các đồ thị $y=f\left( x \right),y=g\left( x \right)$ và hai đường thẳng $x=a,x=b$ (hình phẳng $\left( H \right)$ là phần tô đậm).
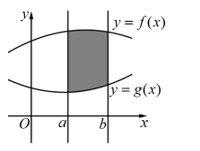
Khi đó, diện tích hình phẳng $\left( H \right)$ được tính theo công thức: $S=\int\limits_{a}^{b}{\left| f\left( x \right)-g\left( x \right) \right|}\text{d}x$.

Khi đó, diện tích hình phẳng $\left( H \right)$ được tính theo công thức: $S=\int\limits_{a}^{b}{\left| f\left( x \right)-g\left( x \right) \right|}\text{d}x$.
PHẦN II. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4.Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S).
Câu 1. Một tên lửa phóng thẳng đứng từ mặt đất với vận tốc ban đầu \(v_0 = 50\text{ m/s}\). Gia tốc của tên lửa (do lực đẩy và trọng lực) phụ thuộc vào thời gian theo công thức \(a(t) = 10 - 2t\) (m/s²). Sau thời gian 10s, tên lửa hết nhiên liệu và tiếp tục bay với gia tốc \(a = -9{,}8\text{ m/s}^2\).
a) Vận tốc của tên lửa đạt được tại thời điểm \(t = 10s\) là 50 m/s.
b) Độ cao của tên lửa đạt tại thời điểm \(t = 10s\) là 660 m.
c) Tên lửa đạt độ cao lớn nhất tại thời điểm \(t = 15s\) (làm tròn kết quả đến hàng đơn vị).
d) Độ cao lớn nhất tên lửa đạt được (làm tròn kết quả đến hàng đơn vị) là 766 m.
| Câu 1 | Giải chi tiết (giải thích) |
| a) Đ | Chọn mốc thời gian tại thời điểm ${{t}_{0}}=0$ là lúc tên lửa được phóng lên với vận tốc ban đầu ${{v}_{0}}=50\,m/s$, $v\left( 0 \right)=50$ và $s\left( 0 \right)=0$. Nguyên hàm của gia tốc là vận tốc nên ta có vận tốc của tên lửa tại thời điểm $t$ là $v\left( t \right)=\int{a\left( t \right)}dt=\int{(10-2t)dt=10t-{{t}^{2}}+C}$. Do $v\left( 0 \right)=50$ nên $C=50$. Suy ra $v\left( t \right)=10t-{{t}^{2}}+50$. Vận tốc tại thời điểm $t=10\,s$ là $v\left( 10 \right)=10.10-{{10}^{2}}+50=50\,\left( m/s \right)$. |
| b) s | Nguyên hàm của vận tốc là quãng đường nên ta có độ cao của tên lửa tại thời điểm $t$ là $s\left( t \right) = \int {v\left( t \right)} dt$ $ = \int {(10t - {t^2} + 50)dt} $ $ = 5{t^2} - \frac{{{t^3}}}{3} + 50t + {C_1}$. Do $s\left( 0 \right)=0$ nên ${{C}_{1}}=0$. Suy ra $s\left( 10 \right)={{5.10}^{2}}-\frac{{{10}^{3}}}{3}+50.10=\frac{2000}{3}$. Độ cao tại thời điểm $t=10\,s$ là $\frac{2000}{3}\left( m \right)$. |
| c) s | $s\left( t \right)=-\frac{{{t}^{3}}}{3}+5{{t}^{2}}+50t$. $\begin{array}{l} s'\left( t \right) = - {t^2} + 10t + 50\\ s'\left( t \right) = 0 \Leftrightarrow \left[ \begin{array}{l} t = 5 + 5\sqrt 3 \,(\,n\,)\\ t = 5 - 5\sqrt 3 \,(l) \end{array} \right. \end{array}$ Bảng biến thiên của hàm số $s(t)$ trên $\left( 0;+\infty \right)$ 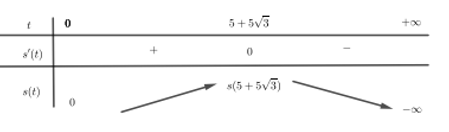
Từ BBT ta có giá trị lớn nhất của $s\left( t \right)=-\frac{{{t}^{3}}}{3}+5{{t}^{2}}+50t$ đạt tại $t=5+5\sqrt{3}\approx 14$. Tên lửa đạt độ cao lớn nhất tại thời điểm $t=14\,s$ (làm tròn kết quả đến hàng đơn vị). |
| d) Đ | $\left( {5 + 5\sqrt 3 } \right)$ $ = - \frac{{{{\left( {5 + 5\sqrt 3 } \right)}^3}}}{3} + 5{\left( {5 + 5\sqrt 3 } \right)^2} + 50\left( {5 + 5\sqrt 3 } \right)$ $ \approx 766$. Độ cao lớn nhất tên lửa đạt được (làm tròn kết quả đến hàng đơn vị) là $766\,m$. |
a) Đường thẳng chứa hành trình của AUV có phương trình \(\dfrac{x - 8}{-4} = \dfrac{y - 6}{-8} = \dfrac{z - 1}{1}\)
b) Mặt cầu (S) có phương trình \((x + 2)^2 + (y - 4)^2 + (z + 2)^2 = 1\)
c) Trên hành trình AUV luôn cách tâm \(K\) một khoảng lớn hơn bán kính \(R\)
d) Hành trình của AUV không đi qua khu vực có thiết bị nhạy cảm hình cầu (S)
| Câu 2 | Giải chi tiết (giải thích) |
| a) Đ | Ta có AUV di chuyển từ $A(8;6;1)$ đến $B(4;-2;2)$. Vector chỉ phương: $\overrightarrow{AB}\text{ }=\text{ }\left( -4,\text{ }-8,\text{ }1 \right)$ Phương trình tham số đường thẳng AB: $\left\{ \begin{align} & x\text{ }=\text{ }8\text{ }-\text{ }4t\text{ } \\ & y\text{ }=\text{ }6\text{ }-\text{ }8t \\ & z\text{ }=\text{ }1\text{ }+\text{ }t \\ \end{align} \right.$ hay $\dfrac{x - 8}{-4} = \dfrac{y - 6}{-8} = \dfrac{z - 1}{1}$ |
| b) Đ | Mặt cầu $(S)$ tâm tại điểm $K(2;-4;2)$, bán kính $R = 1$ nên có phương trình $(x - 2)^2 + (y + 4)^2 + (z - 2)^2 = 1$. |
| c) s | Khoảng cách từ điểm $K(2;-4;2)$ đến đường thẳng AB: $\overrightarrow{AK}\text{ }=\text{ }\left( -6,\text{ }-10,\text{ }1 \right)$ $\overrightarrow{AB}\text{ }=\text{ }\left( -4,\text{ }-8,\text{ }1 \right)$ $\left[ \overrightarrow{AK}\text{ }\text{, }\overrightarrow{AB} \right]\text{ }=\text{ }\left( -2,\text{ }2,\text{ }8 \right)$ $\left| \left[ \overrightarrow{AK}\text{ }\text{, }\overrightarrow{AB} \right] \right|\text{ }=\text{ }\sqrt{72}$, $\left| \overrightarrow{AB} \right|\text{ }=\text{ }9$ $d\text{ }=\text{ }\frac{\sqrt{72}}{9}\text{ }=\text{ }\frac{2\sqrt{2}}{3}\approx \text{ }0,943\text{ }<\text{ }1$ Trên hành trình AUV luôn cách tâm ${K}$ một khoảng nhỏ hơn bán kính ${R}$. |
| d) s | Vì $d < R$ nên hành trình của AUV đi vào vùng có thiết bị nhạy cảm. |
Gọi \(A\) là biến cố “Bài viết thực sự là đạo văn”.
Gọi \(B\) là biến cố “Phần mềm cảnh báo bài viết là đạo văn”.
- Xác suất \(P(B) = 0{,}039\).
- b) Xác suất \(P(A) = 0{,}01\) và \(P(\bar{A}) = 0{,}99\).
- c) Xác suất có điều kiện \(P(A|B) = 0{,}7\).
- d) Trong số những bài viết bị phần mềm cảnh báo là đạo văn, có nhiều khả năng là bài viết chính chủ hơn là đạo văn.

| Câu 3 | Giải chi tiết (giải thích) |
| a) Đ | Áp dụng công thức xác suất toàn phần: $P\left( B \right)=P\left( \overline{A} \right).P\left( B|\overline{A} \right)+P\left( A \right).P\left( B|A \right)$ $=0,99.0,03+0,01.0,98=0,0395$. |
| b) Đ | Theo sơ đồ ta thấy $P\left( A \right)=0,01$ và $P\left( \overline{A} \right)=0,99$. |
| c) s | $P\left( A|B \right)=\frac{P\left( A \right).P\left( B|A \right)}{P\left( B \right)}$ $=\frac{0,01.0,98}{0,0395}=\frac{98}{395}\approx 0,25$. |
| d) Đ | Ta cần so sánh $P\left( A|B \right)$ và $P\left( \overline{A}|B \right)$. Theo câu c) ta có $P\left( A|B \right)=\frac{98}{395}$ suy ra $P\left( {\overline A |B} \right) = 1 - P\left( {A|B} \right)$ $ = 1 - \frac{{98}}{{395}} = \frac{{297}}{{395}} \approx 0,75$. Vậy $P\left( \overline{A}|B \right)>P\left( A|B \right)$ nên d) đúng. |
a) Tập xác định của hàm số là \( \mathbb{R} \setminus \{-2\} \).
b) Hàm số có đạo hàm là \( y' = 1 - \dfrac{9}{(x+2)^2}, \forall x \ne -2 \).
c) Hàm số đồng biến trên các khoảng \( (-\infty; -5) \) và \( (1; +\infty) \).
d) Hàm số có giá trị cực đại lớn hơn giá trị cực tiểu.
| Câu 4 | Giải chi tiết( giải thích) |
| a) Đ | Điều kiện: $x\ne -2$ Tập xác định của hàm số là $D=\mathbb{R}\backslash \left\{ -2 \right\}$. |
| b) Đ | $y'=1-\frac{9}{{{\left( x+2 \right)}^{2}}},\text{ }\forall x\ne -2$ |
| c) Đ | $y'=0\Rightarrow \left[ \begin{align} & x=-5 \\ & x=1 \\ \end{align} \right.$ Bảng biến thiên 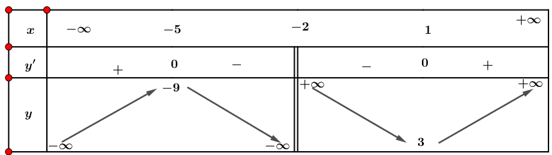
Suy ra hàm số đồng biến trên các khoảng $\left( -\infty ;-5 \right)$ và $\left( 1;+\infty \right)$. |
| d) s | Hàm số có giá trị cực đại bằng $-9$, giá trị cực tiểu bằng $3$. |
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.Câu 1. Tại một khu trung tâm dữ liệu, kỹ sư IT cần kiểm tra kết nối giữa các máy chủ trong hệ thống gồm các trạm \( A, B, C, D, E \). Các tuyến cáp quang nối giữa các trạm được biểu diễn trong sơ đồ sau, với con số ghi trên mỗi tuyến là chiều dài dây cáp (đơn vị: km).

Kỹ sư cần thực hiện một hành trình bắt đầu từ một trạm bất kỳ, đi qua tất cả các tuyến cáp ít nhất một lần và kết thúc tại đúng trạm khởi hành, nhằm đảm bảo toàn bộ hệ thống được kiểm tra. Tổng chiều dài đường đi ngắn nhất mà kỹ sư cần di chuyển là bao nhiêu km?
Từ đồ thị ta thấy có 3 đỉnh $A,B,C$ có bậc lẻ nên không tồn tại một chu trình Euler đi qua tất cả các cạnh đúng một lần. Vậy có cạnh sẽ đi lại lần hai. Tổng trọng số của tất cả các cạnh là: 3 + 4 + 3 + 5 + 2 + 2 + 1=20
Do trọng số các cạnh, nên để đường đi ngắn nhất, các cạnh chọn đi lần 2 sẽ chọn từ các cạnh $AC,BE,BC$. Ta sẽ chọn điểm bắt đầu là 1 trong các đỉnh bậc lẻ $A,B,C,E$.
+) Giả sử ta chọn đỉnh ban đầu là đỉnh $A$, ta sẽ có cách đi như sau để đường đi tối ưu:
A → D → E → C → A → B → E → B → C → A
Chu trình này sẽ đi qua các cạnh $AC$ và $BE$ mỗi cạnh 2 lần, vậy tổng chiều dài lúc này là 20+2+2=24.
+) Nếu chọn đỉnh ban đầu là C, ta có chu trình đi như sau:
C → E → D → A → B → E → B → C → A → C
Chu trình này sẽ đi qua các cạnh $AC$ và $BE$ mỗi cạnh 2 lần, vậy tổng chiều dài lúc này là 20+2+2=24.
Tương tự nếu chọn từ các đỉnh $B,E$ ta cũng chọn được đường đi ngắn nhất là $24$ và cũng phải đi qua các cạnh $AC$ và $BE$ mỗi cạnh 2 lần. Do đó tổng quãng đường nhỏ nhất là $24$.
Do trọng số các cạnh, nên để đường đi ngắn nhất, các cạnh chọn đi lần 2 sẽ chọn từ các cạnh $AC,BE,BC$. Ta sẽ chọn điểm bắt đầu là 1 trong các đỉnh bậc lẻ $A,B,C,E$.
+) Giả sử ta chọn đỉnh ban đầu là đỉnh $A$, ta sẽ có cách đi như sau để đường đi tối ưu:
A → D → E → C → A → B → E → B → C → A
Chu trình này sẽ đi qua các cạnh $AC$ và $BE$ mỗi cạnh 2 lần, vậy tổng chiều dài lúc này là 20+2+2=24.
+) Nếu chọn đỉnh ban đầu là C, ta có chu trình đi như sau:
C → E → D → A → B → E → B → C → A → C
Chu trình này sẽ đi qua các cạnh $AC$ và $BE$ mỗi cạnh 2 lần, vậy tổng chiều dài lúc này là 20+2+2=24.
Tương tự nếu chọn từ các đỉnh $B,E$ ta cũng chọn được đường đi ngắn nhất là $24$ và cũng phải đi qua các cạnh $AC$ và $BE$ mỗi cạnh 2 lần. Do đó tổng quãng đường nhỏ nhất là $24$.
1. Xác định hàm doanh thu:
Doanh thu $R\left( A \right)$ là tổng số tiền thu được từ việc bán sản phẩm.
Giá bán mỗi sản phẩm là $20$ triệu đồng.
Số lượng sản phẩm bán ra là $q\left( A \right)$.
Vậy, hàm doanh thu là: $R\left( A \right)=20\cdot q\left( A \right)=20\left[ 1000+\frac{1013}{5}\ln \left( 1+A \right) \right]$
$\Leftrightarrow R\left( A \right)=20000+4\cdot 1013\ln \left( 1+A \right)$
$\Leftrightarrow R\left( A \right)=20000+4052\ln \left( 1+A \right)$
2. Xác định hàm chi phí:
Tổng chi phí $\left( C \right)$ bao gồm chi phí quảng cáo $\left( A \right)$ và chi phí sản xuất.
Chi phí sản xuất mỗi sản phẩm là $10$ triệu đồng.
Số lượng sản phẩm sản xuất (bằng số lượng bán ra) là $q\left( A \right)$.
Vậy, hàm chi phí sản xuất là: $10\cdot q\left( A \right)$.
Tổng chi phí là: $C(A)=A+10\cdot q\left( A \right)$ $\Leftrightarrow C\left( A \right)=A+10\left[ 1000+\frac{1013}{5}\ln \left( 1+A \right) \right]$
$\Leftrightarrow C\left( A \right)=A+10000+2026\ln \left( 1+A \right)$
3. Xác định hàm lợi nhuận
Lợi nhuận $\left( P \right)$ là hiệu số giữa doanh thu và tổng chi phí.
$P\left( A \right)=R\left( A \right)-C\left( A \right)$ $\Leftrightarrow P\left( A \right)=\left[ 20000+4052\ln \left( 1+A \right) \right]-\left[ A+10000+2026\ln \left( 1+A \right) \right]$
$\Leftrightarrow P\left( A \right)=10000+2026\ln \left( 1+A \right)-A$
4. Ta cần tìm giá trị tối đa của hàm lợi nhuận.
Xét hàm số $P\left( A \right)$ trên $\left( 0;+\infty \right)$ có
${P}'\left( A \right)=\frac{2026}{1+A}-1$, Đặt ${P}'\left( A \right)=0$ $\Leftrightarrow \frac{2026}{1+A}-1=0$ $\Leftrightarrow A=2025$.
Bảng biến thiên
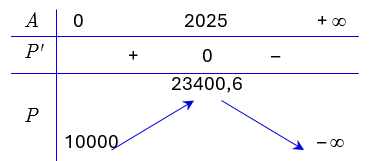
Vậy lợi nhuận tối đa là khoảng $23400.6$ triệu đồng $\approx 23,4$ tỉ đồng.
Doanh thu $R\left( A \right)$ là tổng số tiền thu được từ việc bán sản phẩm.
Giá bán mỗi sản phẩm là $20$ triệu đồng.
Số lượng sản phẩm bán ra là $q\left( A \right)$.
Vậy, hàm doanh thu là: $R\left( A \right)=20\cdot q\left( A \right)=20\left[ 1000+\frac{1013}{5}\ln \left( 1+A \right) \right]$
$\Leftrightarrow R\left( A \right)=20000+4\cdot 1013\ln \left( 1+A \right)$
$\Leftrightarrow R\left( A \right)=20000+4052\ln \left( 1+A \right)$
2. Xác định hàm chi phí:
Tổng chi phí $\left( C \right)$ bao gồm chi phí quảng cáo $\left( A \right)$ và chi phí sản xuất.
Chi phí sản xuất mỗi sản phẩm là $10$ triệu đồng.
Số lượng sản phẩm sản xuất (bằng số lượng bán ra) là $q\left( A \right)$.
Vậy, hàm chi phí sản xuất là: $10\cdot q\left( A \right)$.
Tổng chi phí là: $C(A)=A+10\cdot q\left( A \right)$ $\Leftrightarrow C\left( A \right)=A+10\left[ 1000+\frac{1013}{5}\ln \left( 1+A \right) \right]$
$\Leftrightarrow C\left( A \right)=A+10000+2026\ln \left( 1+A \right)$
3. Xác định hàm lợi nhuận
Lợi nhuận $\left( P \right)$ là hiệu số giữa doanh thu và tổng chi phí.
$P\left( A \right)=R\left( A \right)-C\left( A \right)$ $\Leftrightarrow P\left( A \right)=\left[ 20000+4052\ln \left( 1+A \right) \right]-\left[ A+10000+2026\ln \left( 1+A \right) \right]$
$\Leftrightarrow P\left( A \right)=10000+2026\ln \left( 1+A \right)-A$
4. Ta cần tìm giá trị tối đa của hàm lợi nhuận.
Xét hàm số $P\left( A \right)$ trên $\left( 0;+\infty \right)$ có
${P}'\left( A \right)=\frac{2026}{1+A}-1$, Đặt ${P}'\left( A \right)=0$ $\Leftrightarrow \frac{2026}{1+A}-1=0$ $\Leftrightarrow A=2025$.
Bảng biến thiên

Vậy lợi nhuận tối đa là khoảng $23400.6$ triệu đồng $\approx 23,4$ tỉ đồng.
Bước 1. Người chơi chọn ngẫu nhiên 1 hộp.
Bước 2. Từ hộp đã chọn, người chơi lấy ngẫu nhiên 1 món quà:
- Nếu quà là điện thoại iPhone, người chơi giữ nó và lấy thêm 1 quà nữa từ cùng hộp.
- Nếu quà là tai nghe, trò chơi kết thúc.
Biết rằng người chơi lấy được 2 điện thoại iPhone, tính xác suất để người đó lấy từ hộp màu bạc (làm tròn kết quả đến hàng phần mười).
Tính xác suất lấy được 2 điện thoại iPhone từ mỗi hộp.
+ Hộp vàng: Xác suất lấy được 1 iPhone là $\frac{2}{5}$. Sau khi lấy được 1 iPhone, còn lại 1 iPhone và 3 tai nghe trong hộp. Xác suất lấy được 1 iPhone nữa là $\frac{1}{4}$.
Vậy xác suất lấy được 2 iPhone từ hộp vàng là $\frac{2}{5}\times \frac{1}{4}=\frac{1}{10}$.
+ Hộp bạc: Xác suất lấy được 1 iPhone là $\frac{4}{5}$. Sau khi lấy được 1 iPhone, còn lại 3 iPhone và 1 tai nghe trong hộp. Xác suất lấy được 1 iPhone nữa là $\frac{3}{4}$. Vậy xác suất lấy được 2 iPhone từ hộp bạc là $\frac{4}{5}\times \frac{3}{4}=\frac{3}{5}$.
+ Hộp đồng: Xác suất lấy được 1 iPhone là $\frac{3}{5}$. Sau khi lấy được 1 iPhone, còn lại 2 iPhone và 2 tai nghe trong hộp. Xác suất lấy được 1 iPhone nữa là $\frac{2}{4}=\frac{1}{2}$. Vậy xác suất lấy được 2 iPhone từ hộp đồng là $\frac{3}{5}\times \frac{1}{2}=\frac{3}{10}$.
Tính xác suất chọn hộp bạc, biết lấy được 2 iPhone.
Gọi A là biến cố lấy được 2 iPhone. Gọi B là biến cố chọn hộp bạc. Ta cần tính:
$P\left( B|A \right)=\frac{P\left( A|B \right)P\left( B \right)}{P\left( A \right)}$.
+ $P\left( B \right)=\frac{1}{3}$ (xác suất chọn hộp bạc).
+ $P\left( A|B \right)=\frac{3}{5}$ (xác suất lấy được 2 iPhone từ hộp bạc, đã tính ở trên).
+ P(A) = P(A|B).P(B) + P(A|hopvang).P(hopvang) + P(A|hopdong).P(hopdong) = 3/5.
Vậy $P\left( B|A \right)=\frac{\frac{3}{5}\times \frac{1}{3}}{\frac{1}{3}}=0,6$.
+ Hộp vàng: Xác suất lấy được 1 iPhone là $\frac{2}{5}$. Sau khi lấy được 1 iPhone, còn lại 1 iPhone và 3 tai nghe trong hộp. Xác suất lấy được 1 iPhone nữa là $\frac{1}{4}$.
Vậy xác suất lấy được 2 iPhone từ hộp vàng là $\frac{2}{5}\times \frac{1}{4}=\frac{1}{10}$.
+ Hộp bạc: Xác suất lấy được 1 iPhone là $\frac{4}{5}$. Sau khi lấy được 1 iPhone, còn lại 3 iPhone và 1 tai nghe trong hộp. Xác suất lấy được 1 iPhone nữa là $\frac{3}{4}$. Vậy xác suất lấy được 2 iPhone từ hộp bạc là $\frac{4}{5}\times \frac{3}{4}=\frac{3}{5}$.
+ Hộp đồng: Xác suất lấy được 1 iPhone là $\frac{3}{5}$. Sau khi lấy được 1 iPhone, còn lại 2 iPhone và 2 tai nghe trong hộp. Xác suất lấy được 1 iPhone nữa là $\frac{2}{4}=\frac{1}{2}$. Vậy xác suất lấy được 2 iPhone từ hộp đồng là $\frac{3}{5}\times \frac{1}{2}=\frac{3}{10}$.
Tính xác suất chọn hộp bạc, biết lấy được 2 iPhone.
Gọi A là biến cố lấy được 2 iPhone. Gọi B là biến cố chọn hộp bạc. Ta cần tính:
$P\left( B|A \right)=\frac{P\left( A|B \right)P\left( B \right)}{P\left( A \right)}$.
+ $P\left( B \right)=\frac{1}{3}$ (xác suất chọn hộp bạc).
+ $P\left( A|B \right)=\frac{3}{5}$ (xác suất lấy được 2 iPhone từ hộp bạc, đã tính ở trên).
+ P(A) = P(A|B).P(B) + P(A|hopvang).P(hopvang) + P(A|hopdong).P(hopdong) = 3/5.
Vậy $P\left( B|A \right)=\frac{\frac{3}{5}\times \frac{1}{3}}{\frac{1}{3}}=0,6$.
Đáp số: -1,5
Ta có: $B\in \Delta \Rightarrow B\left( 3+t;-1+2t;4-t \right)$ mà $A\left( 1;0;2 \right)$ là trung điểm BC, suy ra $C\left( -1-t;1-2t;t \right)$.
Lại có $C\in \left( P \right)$, thay vào phương trình mặt phẳng $\left( P \right)$, được:
$\begin{array}{l} 2\left( { - 1 - t} \right) - \left( {1 - 2t} \right) + t + 1 = 0\\ \Leftrightarrow t = 2\\ \to \overrightarrow {BC} = \left( { - 8; - 6;0} \right) = 4\left( { - 2;\frac{{ - 3}}{2};0} \right) \end{array}$
Vậy $a+2b=-1,5$.
Ta có: $B\in \Delta \Rightarrow B\left( 3+t;-1+2t;4-t \right)$ mà $A\left( 1;0;2 \right)$ là trung điểm BC, suy ra $C\left( -1-t;1-2t;t \right)$.
Lại có $C\in \left( P \right)$, thay vào phương trình mặt phẳng $\left( P \right)$, được:
$\begin{array}{l} 2\left( { - 1 - t} \right) - \left( {1 - 2t} \right) + t + 1 = 0\\ \Leftrightarrow t = 2\\ \to \overrightarrow {BC} = \left( { - 8; - 6;0} \right) = 4\left( { - 2;\frac{{ - 3}}{2};0} \right) \end{array}$
Vậy $a+2b=-1,5$.
Đáp số:0,4
Thể tích của khối lập phương là:
${{V}_{\text{lap phuong}}}={{10}^{3}}=1000\text{c}{{\text{m}}^{3}}.$
Vì quả cầu lớn tiếp xúc với tất cả các mặt của lập phương nên đường kính của nó bằng cạnh lập phương, tức là:
${{d}_{\text{lon}}}=10\text{cm}\Rightarrow {{r}_{\text{lon}}}=\frac{10}{2}=5\text{cm}.$
Thể tích của quả cầu lớn là:
${{V}_{\text{lon}}}=\frac{4}{3}\pi {{r}^{3}}=\frac{4}{3}\pi {{(5)}^{3}}=\frac{500}{3}\pi \approx 523,6\text{c}{{\text{m}}^{3}}.$
Giả sử bán kính quả cầu nhỏ là ${r}$. Mỗi quả cầu nhỏ tiếp xúc với ba mặt hộp và tiếp xúc với quả cầu lớn nên tâm của nó nằm trên đoạn nối từ tâm quả cầu lớn đến một đỉnh của hình lập phương.
Khoảng cách từ tâm quả cầu lớn đến một đỉnh hộp là ${R\sqrt{3}}$, còn khoảng cách giữa tâm quả cầu lớn và tâm quả cầu nhỏ là ${R + r}$. Để tiếp xúc tại điểm chung:
$\begin{array}{l} R + r = \sqrt 3 (R - r)\\ \Rightarrow R + r = \sqrt 3 R - \sqrt 3 r\\ \Rightarrow r(1 + \sqrt 3 ) = R(\sqrt 3 - 1)\\ \Rightarrow r = R \cdot \frac{{\sqrt 3 - 1}}{{1 + \sqrt 3 }}. \end{array}$
Rút gọn:
$\frac{{\sqrt 3 - 1}}{{1 + \sqrt 3 }}$ $ = \frac{{{{(\sqrt 3 - 1)}^2}}}{{(1 + \sqrt 3 )(\sqrt 3 - 1)}}$ $ = \frac{{4 - 2\sqrt 3 }}{2}$ $ = 2 - \sqrt 3 ,$ nên $r = R (2 - \sqrt{3}).$
Thay ${R = 5}$: $r=5(2-\sqrt{3})\,\,\text{cm}.$
Thể tích quả cầu nhỏ:
${{V}_{\text{nho}}}=\frac{4}{3}\pi {{r}^{3}}\approx \frac{4}{3}\pi {{(5.(2-\sqrt{3}))}^{3}}\approx 10,07\text{c}{{\text{m}}^{3}}.$
Tổng thể tích ${8}$ quả cầu nhỏ:
$8\cdot {{V}_{\text{nho}}}\approx 8\cdot 10,07=80,56\,\text{c}{{\text{m}}^{3}}.$
Thể tích quả cầu lớn:
${{V}_{\text{lon}}}=\frac{4}{3}\pi {{(5)}^{3}}=\frac{500}{3}\pi \approx 523,6\text{c}{{\text{m}}^{3}}.$
Tổng thể tích các quả cầu:
${{V}_{\text{cau}}}=523,6+80,4=604,16\,\text{c}{{\text{m}}^{3}}.$
Phần thể tích keo cần đổ:
$\begin{array}{l} {V_{{\rm{keo}}}} = 1000 - 604,16\\ \approx 396\,\,{\rm{c}}{{\rm{m}}^3}\\ \approx 0,396\,\,\left( {{\rm{lit}}} \right)\\ \approx {\rm{0}}{\rm{,4 }}\,\,\,\,\left( {{\rm{lit}}} \right) \end{array}$
Thể tích của khối lập phương là:
${{V}_{\text{lap phuong}}}={{10}^{3}}=1000\text{c}{{\text{m}}^{3}}.$
Vì quả cầu lớn tiếp xúc với tất cả các mặt của lập phương nên đường kính của nó bằng cạnh lập phương, tức là:
${{d}_{\text{lon}}}=10\text{cm}\Rightarrow {{r}_{\text{lon}}}=\frac{10}{2}=5\text{cm}.$
Thể tích của quả cầu lớn là:
${{V}_{\text{lon}}}=\frac{4}{3}\pi {{r}^{3}}=\frac{4}{3}\pi {{(5)}^{3}}=\frac{500}{3}\pi \approx 523,6\text{c}{{\text{m}}^{3}}.$
Giả sử bán kính quả cầu nhỏ là ${r}$. Mỗi quả cầu nhỏ tiếp xúc với ba mặt hộp và tiếp xúc với quả cầu lớn nên tâm của nó nằm trên đoạn nối từ tâm quả cầu lớn đến một đỉnh của hình lập phương.
Khoảng cách từ tâm quả cầu lớn đến một đỉnh hộp là ${R\sqrt{3}}$, còn khoảng cách giữa tâm quả cầu lớn và tâm quả cầu nhỏ là ${R + r}$. Để tiếp xúc tại điểm chung:
$\begin{array}{l} R + r = \sqrt 3 (R - r)\\ \Rightarrow R + r = \sqrt 3 R - \sqrt 3 r\\ \Rightarrow r(1 + \sqrt 3 ) = R(\sqrt 3 - 1)\\ \Rightarrow r = R \cdot \frac{{\sqrt 3 - 1}}{{1 + \sqrt 3 }}. \end{array}$
Rút gọn:
$\frac{{\sqrt 3 - 1}}{{1 + \sqrt 3 }}$ $ = \frac{{{{(\sqrt 3 - 1)}^2}}}{{(1 + \sqrt 3 )(\sqrt 3 - 1)}}$ $ = \frac{{4 - 2\sqrt 3 }}{2}$ $ = 2 - \sqrt 3 ,$ nên $r = R (2 - \sqrt{3}).$
Thay ${R = 5}$: $r=5(2-\sqrt{3})\,\,\text{cm}.$
Thể tích quả cầu nhỏ:
${{V}_{\text{nho}}}=\frac{4}{3}\pi {{r}^{3}}\approx \frac{4}{3}\pi {{(5.(2-\sqrt{3}))}^{3}}\approx 10,07\text{c}{{\text{m}}^{3}}.$
Tổng thể tích ${8}$ quả cầu nhỏ:
$8\cdot {{V}_{\text{nho}}}\approx 8\cdot 10,07=80,56\,\text{c}{{\text{m}}^{3}}.$
Thể tích quả cầu lớn:
${{V}_{\text{lon}}}=\frac{4}{3}\pi {{(5)}^{3}}=\frac{500}{3}\pi \approx 523,6\text{c}{{\text{m}}^{3}}.$
Tổng thể tích các quả cầu:
${{V}_{\text{cau}}}=523,6+80,4=604,16\,\text{c}{{\text{m}}^{3}}.$
Phần thể tích keo cần đổ:
$\begin{array}{l} {V_{{\rm{keo}}}} = 1000 - 604,16\\ \approx 396\,\,{\rm{c}}{{\rm{m}}^3}\\ \approx 0,396\,\,\left( {{\rm{lit}}} \right)\\ \approx {\rm{0}}{\rm{,4 }}\,\,\,\,\left( {{\rm{lit}}} \right) \end{array}$

Hai đường cong trong hình là một phần của đồ thị hàm số có dạng \( y = \frac{ax + b}{cx + d} \), đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số này đều cách điểm \(A\) một khoảng bằng 5 m. Đồ thị giao với cạnh \(AB\) tại điểm \(E\) thỏa mãn \( \frac{AE}{AB} = \frac{7}{15} \). Diện tích phần in nội dung quảng cáo là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)?
Đáp án: 64,2
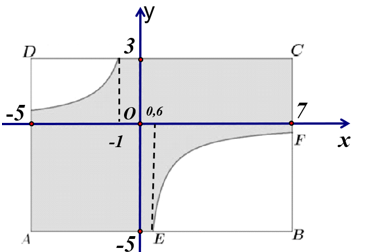
Chọn hệ trục tọa độ $\text{Ox}y$trùng với hai tiệm cận như hình vẽ
Suy ra: $A\left( -5;-5 \right);B\left( 7;-5 \right);C\left( 7;3 \right)$
Tiệm cận đứng $x=\frac{-d}{c}=0\Rightarrow d=0$
Tiệm cận ngang $y=\frac{a}{c}=0\Rightarrow a=0$ $\Rightarrow y=\frac{b}{c\text{x}}\,\,\,\left( C \right)$
Ta có:
$\begin{array}{l} \frac{{A{\rm{E}}}}{{AB}} = \frac{{{x_E} - {x_A}}}{{12}} = \frac{{{x_E} + 5}}{{12}} = \frac{7}{{15}}\\ \Rightarrow {x_E} = \frac{3}{5} = 0,6 \Rightarrow E\left( {0,6; - 5} \right) \end{array}$
thay vào phương trình $\,\left( C \right)\Rightarrow -5=\frac{b}{c.0,6}\Rightarrow b=-3c$.Khi đó: $y=\frac{-3}{x}$.
Gọi $K$là giao điểm của đồ thị $\left( C \right)$với đường thẳng $y=3$$\Rightarrow K\left( -1;3 \right)$
Từ hình vẽ ta có
$\begin{array}{l} {S_1} = \int\limits_{ - 5}^{ - 1} {\left( {3 + \frac{3}{x}} \right)dx} \\ = \left. {\left( {3x + 3\ln \left| x \right|} \right)} \right|_{ - 5}^{ - 1}\\ = 12 - 3\ln 5\\ {S_2} = \int\limits_{0,6}^7 {\left( {\frac{{ - 3}}{x} + 5} \right)dx} \\ = \left. {\left( { - 3\ln \left| x \right| + 5x} \right)} \right|_{0,6}^7\\ = 32 + 3\ln \frac{3}{{35}} \end{array}$
Diện tích phần in nội dung quảng cáo (phần tô đậm) là:
$\begin{array}{l} S = {S_{hcnABCD}} - {S_1} - {S_2}\\ = 96 - 12 + 3\ln 5 - 32 + 3\ln \frac{3}{{35}}\\ = 52 + 3\ln \frac{{175}}{3} \approx 64,2\left( {{m^2}} \right) \end{array}$

Chọn hệ trục tọa độ $\text{Ox}y$trùng với hai tiệm cận như hình vẽ
Suy ra: $A\left( -5;-5 \right);B\left( 7;-5 \right);C\left( 7;3 \right)$
Tiệm cận đứng $x=\frac{-d}{c}=0\Rightarrow d=0$
Tiệm cận ngang $y=\frac{a}{c}=0\Rightarrow a=0$ $\Rightarrow y=\frac{b}{c\text{x}}\,\,\,\left( C \right)$
Ta có:
$\begin{array}{l} \frac{{A{\rm{E}}}}{{AB}} = \frac{{{x_E} - {x_A}}}{{12}} = \frac{{{x_E} + 5}}{{12}} = \frac{7}{{15}}\\ \Rightarrow {x_E} = \frac{3}{5} = 0,6 \Rightarrow E\left( {0,6; - 5} \right) \end{array}$
thay vào phương trình $\,\left( C \right)\Rightarrow -5=\frac{b}{c.0,6}\Rightarrow b=-3c$.Khi đó: $y=\frac{-3}{x}$.
Gọi $K$là giao điểm của đồ thị $\left( C \right)$với đường thẳng $y=3$$\Rightarrow K\left( -1;3 \right)$
Từ hình vẽ ta có
$\begin{array}{l} {S_1} = \int\limits_{ - 5}^{ - 1} {\left( {3 + \frac{3}{x}} \right)dx} \\ = \left. {\left( {3x + 3\ln \left| x \right|} \right)} \right|_{ - 5}^{ - 1}\\ = 12 - 3\ln 5\\ {S_2} = \int\limits_{0,6}^7 {\left( {\frac{{ - 3}}{x} + 5} \right)dx} \\ = \left. {\left( { - 3\ln \left| x \right| + 5x} \right)} \right|_{0,6}^7\\ = 32 + 3\ln \frac{3}{{35}} \end{array}$
Diện tích phần in nội dung quảng cáo (phần tô đậm) là:
$\begin{array}{l} S = {S_{hcnABCD}} - {S_1} - {S_2}\\ = 96 - 12 + 3\ln 5 - 32 + 3\ln \frac{3}{{35}}\\ = 52 + 3\ln \frac{{175}}{3} \approx 64,2\left( {{m^2}} \right) \end{array}$
