TangGiap giới thiệu tới bạn đề thi thử tốt nghiệp THPT 2025 môn Toán – Trường THPT Chuyên Lam Sơn, Thanh Hóa. Bám sát cấu trúc đề minh họa của Bộ, có đáp án và lời giải chi tiết để học sinh ôn luyện hiệu quả.
Câu 1. Cho cấp số cộng $(u_n)$ với $u_1 = 9$ và công sai $d = 2$. Giá trị của $u_2$ bằng
A. 11.
B. $\dfrac{9}{2}$
C. 18.
D. 7.
Câu 2. Trong không gian với hệ tọa độ $Oxyz$, cho đường thẳng $d: \dfrac{x - 3}{2} = \dfrac{y - 4}{-5} = \dfrac{z + 1}{3}$. Vector nào dưới đây là một vector chỉ phương của $d$?
A. $\vec{u}_1 (2; 4; -1)$.
B. $\vec{u}_2 (2; -5; 3)$.
C. $\vec{u}_3 (2; 5; 3)$.
D. $\vec{u}_4 (3; 4; 1)$.
Câu 3. Trong không gian với hệ tọa độ $Oxyz$, phương trình nào sau đây là phương trình mặt cầu (S) tâm $A(2;1;0)$, đi qua điểm $B(0;1;2)$?
A. $(x + 2)^2 + (y + 1)^2 + z^2 = 8$.
B. $(x - 2)^2 + (y - 1)^2 + z^2 = 8$.
C. $(x - 2)^2 + (y - 1)^2 + z^2 = 64$.
D. $(x + 2)^2 + (y + 1)^2 + z^2 = 64$.
Câu 4. Biết $\int\limits_0^1 f(x)\,dx = 3$ và $\int\limits_0^1 g(x)\,dx = -2$. Khi đó $\int\limits_0^1 \left[ f(x) + g(x) \right] dx$ bằng
A. 1.
B. 5.
C. -1.
D. -6.
Câu 5. Hàm số nào dưới đây đồng biến trên tập xác định của nó?
A. $y = \left( \dfrac{1}{\pi} \right)^x$.
B. $y = \left( \dfrac{2}{3} \right)^x$.
C. $y = \left( \sqrt{3} \right)^x$.
D. $y = (0{,}5)^x$.
Câu 6. Trên khoảng $(-\infty; +\infty)$, hàm số $F(x) = \dfrac{1}{2} \sin 2x$ là một nguyên hàm của hàm số nào dưới đây?
A. $f_3(x) = -\dfrac{1}{2} \cos 2x$.
B. $f_4(x) = \dfrac{1}{4} \cos 2x$.
C. $f_2(x) = \cos 2x$.
D. $f_1(x) = -\cos 2x$.
Câu 7. Cho hàm số $y = f(x)$ có đồ thị như hình vẽ:
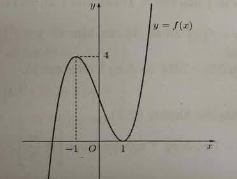
Điểm cực đại của đồ thị hàm số là
A. $x = -1$.
B. $y = 4$.
C. $(1; 0)$.
D. $(-1; 4)$.
Câu 8. Một siêu thị thống kê số tiền (đơn vị: chục nghìn đồng) mà 44 khách hàng mua hàng ở siêu thị đó trong một ngày. Số liệu được cho ở Bảng.
Biết số trung bình của mẫu số liệu đã cho là $\bar{x} = 53{,}18$. Phương sai của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần mười) là
A. $s^2 = 46{,}12$.
B. $s^2 = 46{,}1$.
C. $s^2 = 46{,}21$.
D. $s^2 = 46{,}2$.
Câu 9. Tập nghiệm của bất phương trình $\log_2 (3x - 1) < 3$ là
A. $\left( \dfrac{1}{3} ; \dfrac{10}{3} \right)$
B. $(-\infty; 3)$
C. $\left( \dfrac{1}{3} ; \dfrac{10}{3} \right]$
D. $\left( -\infty ; \dfrac{10}{3} \right)$
Câu 10. Cho hàm số $y = f(x)$ có bảng biến thiên như sau
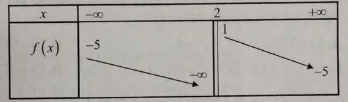
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A. 4
B. 2
C. 3
D. 1
Câu 11. Trong không gian với hệ tọa độ $Oxyz$, cho hai vectơ $\vec{a}$ và $\vec{b}$ cùng có độ dài bằng 1. Biết góc giữa hai vectơ này bằng $120^\circ$. Hãy tính $T = \vec{a} \cdot \vec{b}$.
A. $T = -1$
B. $T = -\dfrac{1}{2}$
C. $T = \dfrac{\sqrt{3}}{2}$
D. $T = -\dfrac{\sqrt{3}}{2}$
Câu 12. Cho hình chóp $S.ABC$ có $SA$ vuông góc với mặt phẳng $(ABC)$ và đáy $ABC$ vuông tại $B$. Gọi $M$ là trung điểm của $SB$. Đường thẳng đi qua hai điểm nào sau đây vuông góc với mặt phẳng $(SAB)$.
A. $A;C$
B. $S;C$
C. $B;C$
D. $M;C$
Câu 1. Cho hàm đa thức $y = f(x)$ có đồ thị của hàm số $y = f'(x)$ là đường cong trong hình vẽ bên.
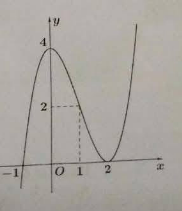
a) Hàm số $g(x) = f(x) - 2025x + 2024$ có đúng 2 điểm cực trị.
b) $\min f(x) = f(-1)$.
c) Hàm số $f(x)$ nghịch biến trên khoảng $(0;2)$.
d) Phương trình $f'( \cos x ) = 3$ có đúng 5 nghiệm thuộc $\left[0; \dfrac{5\pi}{2} \right]$.
Câu 2: Một robot tự hành ở một cảng vận chuyển công nghệ cao bắt đầu di chuyển từ vị trí nghỉ tại điểm $A$. Robot di chuyển như sau: Trong giai đoạn đầu, robot tăng tốc đều từ vận tốc $0 \, (m/s)$ đến $10 \, (m/s)$ trong thời gian chưa biết $t_1$ giây theo hàm số vận tốc $v_1(t) = at$ (a gọi là gia tốc trong giai đoạn này, $a \, (m/s^2)$). Sau đó, robot tiếp tục di chuyển với vận tốc không đổi trong 40 giây. Cuối cùng, robot giảm tốc đều từ $10 \, (m/s)$ và dừng lại đúng tại bảng chỉ dẫn điểm $B$ với thời gian $t_2$ giây theo hàm vận tốc $v_2(t) = 10 - bt$ (b gọi là gia tốc trong thời gian hãm, $b \, (m/s^2)$). Toàn bộ quá trình vận chuyển diễn ra trong khoảng thời gian là 70 giây.
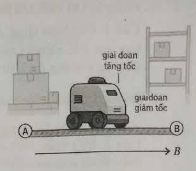
Xét tính đúng sai của các mệnh đề sau:
a) Nếu gia tốc $a = 0{,}5 \, (m/s^2)$, thời gian tăng tốc $t_1$ bé hơn 21 giây.
b) Nếu gia tốc $b = 0{,}8 \, (m/s^2)$, thời gian giảm tốc $t_2$ lớn hơn 13 giây.
c) $\dfrac{1}{a} + \dfrac{1}{b} = \dfrac{5}{4}$.
d) Tổng quãng đường mà robot đã di chuyển từ $A$ đến $B$ là $550 \, m$.
Câu 3: Một trường THPT Chuyên cử một đội tuyển gồm 90 học sinh tham dự kỳ thi Học sinh giỏi cấp Quốc gia. Đội tuyển có cả học sinh nam và học sinh nữ. Sau kỳ thi, kết quả thống kê cho thấy có 85 học sinh đạt huy chương. Thông tin chi tiết như sau:
a) Xác suất chọn được một học sinh nữ là $\dfrac{4}{9}$.
b) Xác suất chọn được một học sinh nam và đạt huy chương là $\dfrac{7}{15}$.
c) Biết học sinh được chọn là nam, xác suất học sinh đó đạt huy chương là $\dfrac{24}{25}$.
d) Biết rằng học sinh được chọn đã đạt huy chương, xác suất học sinh đó là nữ là $\dfrac{37}{85}$.
Câu 4. Trong không gian $Oxyz$, cho hình lập phương $ABCD.A'B'C'D'$ có $A(0;0;0), B(3;0;0), D(0;3;0), A'(0;0;3)$. Gọi $P$ là trung điểm $B'C'$, $K$ là điểm thuộc mặt phẳng $(Oxz)$.
a) Tọa độ điểm $C$ là $(3;3;0)$.
b) Trọng tâm của tam giác $PCD$ có tọa độ là $\left( \dfrac{2}{3}; \dfrac{5}{4};1 \right)$
c) Giá trị nhỏ nhất của biểu thức $\sqrt{KP^2 + KC^2 + KD^2}$ là $\dfrac{5}{2}$.
d) Góc giữa hai đường thẳng $AP$ và $BC'$ bằng $60^\circ$.
Hạ $HK \perp AC$ ($K$ là trung điểm của $AO$) và hạ $HI \perp SK$ thì $HI$ là khoảng cách từ $H$ đến mặt phẳng $(SAC)$.
Tính $HI$.
Ta có : $BD = 2\sqrt{5}\sqrt{3} = 2\sqrt{15}$ nên $BO = \sqrt{15}$. Vậy $HK = \frac{1}{2}BO = \frac{\sqrt{15}}{2}$.
$SH$ là chiều cao trong tam giác đều $SAB$ nên $SH = \frac{AB\sqrt{3}}{2} = \sqrt{15}$.
Nên $\frac{1}{HI^2} - \frac{1}{HK^2} + \frac{1}{HS^2} = \frac{4}{15} - \frac{1}{15} = \frac{3}{15}$. Vậy $HI^2 = 3$.
Câu 2. Cho hàm số $y = \dfrac{x^2 - 2x - 2}{x + 1}$ có đồ thị $(C)$. Gọi $A, B$ là hai điểm cực trị của đồ thị $(C)$. Tính bình phương của độ dài đoạn thẳng $AB$.
Câu 3. Mỗi tuần, một cửa hàng bán điện thoại di động trung bình bán được 1000 điện thoại A với giá 14 triệu đồng một cái. Biết rằng, nếu cứ giảm giá bán 500 nghìn đồng/1 cái, số lượng điện thoại A bán ra sẽ tăng thêm khoảng 100 cái mỗi tuần. Biết rằng nếu bán $x$ cái điện thoại A thì giá mỗi cái là $p(x)$ (triệu đồng) và hàm chi phí hàng tuần $C(x) = 12000 - 3x$ (triệu đồng). Để lợi nhuận là lớn nhất, cửa hàng nên bán mỗi cái điện thoại A với giá bao nhiêu (triệu đồng)?
Câu 4. Trong lớp chuyên Toán trường Chuyên Lam Sơn có 36 bạn học cả năm (mỗi bạn chỉ được xếp nhiều nhất một bạn), được xếp thành 4 hàng và 9 cột (các hàng được đánh số từ trên xuống dưới theo thứ tự từ 1 đến 4, các cột được đánh số từ trái qua phải theo thứ tự từ 1 đến 9). Biết số thứ tự của lớp là 35. Sau học kì I, thầy chủ nhiệm xếp lại ngồi cho các bạn học sinh theo sinh trong lớp. Giả sử trước thời điểm chuyển chỗ bạn ngồi ở hàng thứ $m$, cột thứ $n$ và sau khi chuyển chỗ bạn đó ngồi ở hàng thứ $a$, cột thứ $b$, thì ta gán cho bạn đó số nguyên là $(a + a_1) - (m + n)$. Nếu bạn đầu bạn trống ở vị trí $(1;1)$, sau khi chuyển chỗ bạn trống ở vị trí $(2;5)$ thì tổng của 35 số nguyên được gán cho 35 bạn là bao nhiêu?
Câu 5: Trong một trung tâm logistics, người ta cần thiết kế một thùng hàng hình hộp chữ nhật để đóng gói và vận chuyển thiết bị điện tử. Tổng diện tích các mặt ngoài của thùng bằng 36 m² (bao gồm cả mặt đáy, mặt nắp và 4 mặt bên). Để đảm bảo khả năng đóng gói vừa và thiết bị, đường chéo không gian của thùng phải dài 6 mét. Thể tích lớn nhất có thể của thùng hàng này là bao nhiêu (tính theo đơn vị mét khối, làm tròn đến hàng phần chục)?

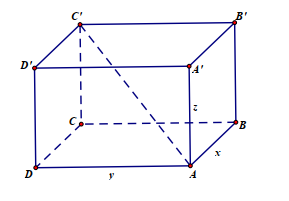
Cách 1.
Gọi $x, \ y, \ z$ lần lượt là độ dài của các cạnh $AB, \ AD, \ AA'$.
Diện tích tất cả các mặt là $S_p = 2(xy + yz + zx) = 36 \Leftrightarrow xy + yz + zx = 18, \tag{1}$
Độ dài đường chéo $AC' = \sqrt{x^2 + y^2 + z^2} = 6 \Leftrightarrow x^2 + y^2 + z^2 = 36.$
Suy ra $(x + y + z)^2 = x^2 + y^2 + z^2 + 2(xy + yz + zx) = 72 \Leftrightarrow x + y + z = 6\sqrt{2}, \tag{2}$
Từ (2) ta có $y + z = 6\sqrt{2} - x$. Do đó, kết hợp với (1) ta được $ yz = 18 - x(y + z) = 18 - x\left(6\sqrt{2} - x\right) = x^2 - 6\sqrt{2}x + 18. $
Ta luôn có $(y + z)^2 \ge 4yz,\ \forall y, z$ nên $ (6\sqrt{2} - x)^2 \ge 4\left(x^2 - 6\sqrt{2}x + 18\right) \Leftrightarrow 3x^2 - 12\sqrt{2}x \le 0 \Leftrightarrow 0 \le x \le 4\sqrt{2}. $
Thể tích của khối hộp chữ nhật là $V = xyz = x\left(x^2 - 6\sqrt{2}x + 18\right) = x^3 - 6\sqrt{2}x^2 + 18x$.
Bài toán trở thành tìm giá trị lớn nhất của hàm số $f(x) = x^3 - 6\sqrt{2}x^2 + 18x$ trên đoạn $\left[0; 4\sqrt{2} \right]$.
Ta có $f'(x) = 3x^2 - 12\sqrt{2}x + 18$ và $f'(x) = 0 \Leftrightarrow \begin{cases} x = \sqrt{2} \in \left[0; 4\sqrt{2} \right] \\ x = 3\sqrt{2} \in \left[0; 4\sqrt{2} \right]. \end{cases}$
Ta tính được $f(0) = 0; \ f(4\sqrt{2}) = 8\sqrt{2}; \ f(\sqrt{2}) = 8\sqrt{2}; \ f(3\sqrt{2}) = 0$.
Với $x = \sqrt{2}$ thì $ \begin{cases} y + z = 5\sqrt{2} \\ yz = 8 \end{cases}. \text{Như thế } (x; y; z) \in \left\{ (\sqrt{2}; 4\sqrt{2}; \sqrt{2}), (\sqrt{2}; \sqrt{2}; 4\sqrt{2}) \right\}. $
Với $x = 4\sqrt{2}$ thì $ \begin{cases} y + z = 2\sqrt{2} \\ yz = 2 \end{cases}. \text{Như thế } (x; y; z) = (4\sqrt{2}; \sqrt{2}; \sqrt{2}). $
Vậy thể tích của khối hộp chữ nhật lớn nhất là $8\sqrt{2} \approx 11{,}3m^3$ khi $(x; y; z) = (\sqrt{2}; 4\sqrt{2}; \sqrt{2})$ và các hoán vị của nó.
Cách 2.
Gọi $x, \ y, \ z$ lần lượt là độ dài của các cạnh $AB, \ AD, \ AA'$.
Diện tích tất cả các mặt là $S_p = 2(xy + yz + zx) = 36 \Leftrightarrow xy + yz + zx = 18, \tag{1}$
Độ dài đường chéo $AC' = \sqrt{x^2 + y^2 + z^2} = 6 \Leftrightarrow x^2 + y^2 + z^2 = 36.$
Suy ra $(x + y + z)^2 = x^2 + y^2 + z^2 + 2(xy + yz + zx) = 72 \Leftrightarrow x + y + z = 6\sqrt{2}, \tag{2}$
Thể tích của khối hộp chữ nhật là $V = xyz, \tag{3}$
Từ (1), (2) và (3) suy ra $x, \ y, \ z$ là 3 nghiệm của phương trình
$X^3 - 6\sqrt{2}X^2 + 18X - V = 0 \Leftrightarrow V = X^3 - 6\sqrt{2}X^2 + 18X, \tag{4}$
Bảng biến thiên của hàm số $f(X) = X^3 - 6\sqrt{2}X^2 + 18X$ trên $(0; 6\sqrt{2})$ như sau

Dựa vào bảng biến thiên, giá trị lớn nhất của $V$ để phương trình $(4)$ có $3$ nghiệm (không cần phân biệt) trên khoảng $(0,6\sqrt{2})$ là $8\sqrt{2}$.
Vậy thể tích của khối hộp chữ nhật lớn nhất là $8\sqrt{2} = 11.3m^3$ khi $(x:y:z)=(\sqrt{2}:4\sqrt{2}:\sqrt{2})$ và các hoán vị của nó.
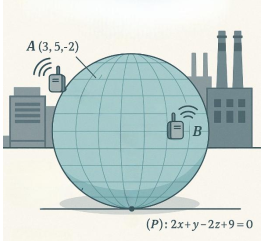
Câu 6: Một công ty xây dựng một hệ thống Giám sát môi trường tại khu công nghiệp. Hai cảm biến không dây được đặt tại hai vị trí $A, B$ trong không gian 3 chiều để thu thập dữ liệu không khí. Để đảm bảo tín hiệu truyền giữa hai cảm biến ổn định, công ty thiết kế một bóng bảo vệ tín hiệu hình cầu có đường nhưng luôn đi qua cả hai cảm biến tại $A$ và $B$. Bóng này cần tiếp xúc với mặt đất để đảm bảo tính ổn định. Giả sử trong không gian với hệ tọa độ $Oxyz$, tọa độ các điểm lần lượt là $A(3;5;-2), B(-1;3;2)$, mặt đất được mô tả bằng mặt phẳng: $(P): 2x + y - 2z + 9 = 0$. Trong quá trình mô phỏng, điểm tiếp xúc giữa bóng bảo vệ và mặt đất (gọi là $C$) thay đổi. Kỹ sư cần xác định khoảng cách từ gốc tọa độ $O(0,0,0)$ đến điểm tiếp xúc $C$ để đánh giá mức độ ảnh hưởng từ vị trí thiết bị. Gọi $m_1$ là giá trị lớn nhất, và $m_2$ là giá trị nhỏ nhất của độ dài $OC$. Tính giá trị $m_1^2 + m_2^2$.
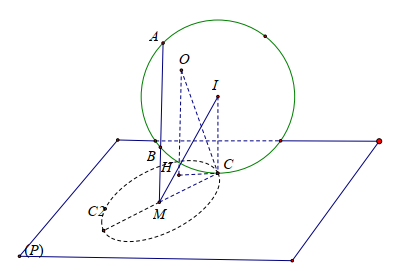
$\left\{ {\begin{array}{*{20}{l}} {\overrightarrow {AB} = ( - 4; - 2;4) = - 2(2;1; - 2)}\\ {\overrightarrow {{n_p}} = (2;1; - 2)} \end{array}} \right.$ $ \Rightarrow \overrightarrow {AB} ,\overrightarrow {{n_p}} $ cùng phương lên $\overrightarrow {AB} \bot (P),\;AB = 6$
$d\left( {A;(P)} \right) = \frac{{|2.3 + 5 - 2.( - 2) + 9|}}{{\sqrt {{2^2} + {1^2} + {{( - 2)}^2}} }} = 8{\rm{ }}$
và ${\rm{ }}d\left( {B;(P)} \right) = \frac{{|2.( - 1) + 3 - 2.2 + 9|}}{{\sqrt {{2^2} + {1^2} + {{( - 2)}^2}} }} = 2$
$AB \cap (P) = M$ suy ra M cố định
Do $(P)$ tiếp xúc với mặt cầu $(S)$ tại $C$ nên $MC \perp IC$ tại $C$
$ \Rightarrow MA \cdot MB = M{C^2},$ ta có ${\rm{ }}\left\{ {\begin{array}{*{20}{l}} {MA = d\left( {A;(P)} \right) = 8}\\ {MB = d\left( {B;(P)} \right) = 2} \end{array}} \right.$ $ \Leftrightarrow M{C^2} = 16$
$ \Leftrightarrow MC = 4$
Vậy C thuộc đường tròn tâm M bán kính r = MC = 4
Ta có: $\overrightarrow {AB} :\left\{ {\begin{array}{*{20}{l}} {x = 3 + 2t}\\ {y = 5 + t}\\ {z = - 2 - 2t} \end{array}} \right.,\quad $ $M = AB \cap (P) \Rightarrow M\left( {\frac{{ - 7}}{3},\frac{7}{3},\frac{{10}}{3}} \right)$
Gọi $H$ là hình chiếu của $O$ lên mặt phẳng $(P) \Rightarrow d\left(O, (P)\right) = 3$, $OH :$ $ \begin{cases} x = 2t \\ y = t \\ z = -2t \end{cases} $
$H = OH \cap (P) \Leftrightarrow H( - 2; - 1;2),\;$ $HM = \sqrt {13} < 4{\rm{ }}$ nên H nằm trong đường tròn tâm M bán kính $r = MC = 4.{\rm{ }}$
${\rm{Suy ra }}OC = \sqrt {O{H^2} + H{C^2}} = \sqrt {9 + H{C^2}} $
=> OC đạt min hoặc max <=> HC đạt min hoặc max
$\left\{ {\begin{array}{*{20}{l}} {H{C_{{\rm{min}}}} = |HM - r| = 4 - \sqrt {13} }\\ {H{C_{{\rm{max}}}} = HM + r = 4 + \sqrt {13} } \end{array}} \right.$ $ \Rightarrow \left\{ {\begin{array}{*{20}{l}} {O{C_{{\rm{min}}}} = \sqrt {9 + {{(4 - \sqrt {13} )}^2}} = {m_2}}\\ {O{C_{{\rm{max}}}} = \sqrt {9 + {{(4 + \sqrt {13} )}^2}} = {m_1}} \end{array}} \right.$
Vậy $m_1^2 + m_2^2 = 76$
Phần 1. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu chỉ chọn một phương án.Câu 1. Cho cấp số cộng $(u_n)$ với $u_1 = 9$ và công sai $d = 2$. Giá trị của $u_2$ bằng
A. 11.
B. $\dfrac{9}{2}$
C. 18.
D. 7.
Chọn A.
Ta có: u₂ = u₁ + d = 9 + 2 = 11.
Ta có: u₂ = u₁ + d = 9 + 2 = 11.
A. $\vec{u}_1 (2; 4; -1)$.
B. $\vec{u}_2 (2; -5; 3)$.
C. $\vec{u}_3 (2; 5; 3)$.
D. $\vec{u}_4 (3; 4; 1)$.
Chọn B
Đúng lý thuyết chọn đáp án B
Đúng lý thuyết chọn đáp án B
A. $(x + 2)^2 + (y + 1)^2 + z^2 = 8$.
B. $(x - 2)^2 + (y - 1)^2 + z^2 = 8$.
C. $(x - 2)^2 + (y - 1)^2 + z^2 = 64$.
D. $(x + 2)^2 + (y + 1)^2 + z^2 = 64$.
Chọn A
Vì mặt cầu $(S)$ có tâm $A(2;1;0)$, đi qua điểm $B(0;1;2)$ nên mặt cầu $(S)$ có tâm $A(2;1;0)$ và có bán kính $R = AB$.
Ta có: $\overrightarrow{AB}(-2;0;2)$. Suy ra $R = |\overrightarrow{AB}| = 2\sqrt{2}$.
Vậy : $(S) : (x-2)^2 + (y-1)^2 + z^2 = 8$.
Vì mặt cầu $(S)$ có tâm $A(2;1;0)$, đi qua điểm $B(0;1;2)$ nên mặt cầu $(S)$ có tâm $A(2;1;0)$ và có bán kính $R = AB$.
Ta có: $\overrightarrow{AB}(-2;0;2)$. Suy ra $R = |\overrightarrow{AB}| = 2\sqrt{2}$.
Vậy : $(S) : (x-2)^2 + (y-1)^2 + z^2 = 8$.
A. 1.
B. 5.
C. -1.
D. -6.
$\int_{0}^{1} \left[ f(x) + g(x) \right] dx = \int_{0}^{1} f(x) \, dx + \int_{0}^{1} g(x) \, dx = 3 + (-2) = 1.$
Chọn B
Chọn B
A. $y = \left( \dfrac{1}{\pi} \right)^x$.
B. $y = \left( \dfrac{2}{3} \right)^x$.
C. $y = \left( \sqrt{3} \right)^x$.
D. $y = (0{,}5)^x$.
Chọn C
Hàm số $y = a^x$ đồng biến nếu $a > 1$ và nghịch biến nếu $0 < a < 1$.
Hàm số $y = a^x$ đồng biến nếu $a > 1$ và nghịch biến nếu $0 < a < 1$.
A. $f_3(x) = -\dfrac{1}{2} \cos 2x$.
B. $f_4(x) = \dfrac{1}{4} \cos 2x$.
C. $f_2(x) = \cos 2x$.
D. $f_1(x) = -\cos 2x$.
Chọn C
Ta có $\left( \dfrac{1}{2} \sin 2x \right)' = \cos 2x$.
Ta có $\left( \dfrac{1}{2} \sin 2x \right)' = \cos 2x$.

Điểm cực đại của đồ thị hàm số là
A. $x = -1$.
B. $y = 4$.
C. $(1; 0)$.
D. $(-1; 4)$.
Chọn D
| Nhóm | Giá trị đại diện | Tần số |
|---|---|---|
| [40;45) | 42,5 | 4 |
| [45;50) | 47,5 | 14 |
| [50;55) | 52,5 | 8 |
| [55;60) | 57,5 | 10 |
| [60;65) | 62,5 | 6 |
| [65;70) | 67,5 | 2 |
| n = 44 |
A. $s^2 = 46{,}12$.
B. $s^2 = 46{,}1$.
C. $s^2 = 46{,}21$.
D. $s^2 = 46{,}2$.
Chọn B
Ta có: 4(42,5 - 53,18)$^2$ + 14(47,5 - 53,18)$^2$ + 8(52,5 - 53,18)$^2$ + 10(57,5 - 53,18)$^2$ + 6(62,5 - 53,18)$^2$ + 2(67,5 - 53,18)$^2$ = 2029,5456.
Vậy phương sai của mẫu số liệu ghép nhóm trên là: $ s^2 = \dfrac{2029{,}5456}{44} \approx 46{,}1 $
Ta có: 4(42,5 - 53,18)$^2$ + 14(47,5 - 53,18)$^2$ + 8(52,5 - 53,18)$^2$ + 10(57,5 - 53,18)$^2$ + 6(62,5 - 53,18)$^2$ + 2(67,5 - 53,18)$^2$ = 2029,5456.
Vậy phương sai của mẫu số liệu ghép nhóm trên là: $ s^2 = \dfrac{2029{,}5456}{44} \approx 46{,}1 $
A. $\left( \dfrac{1}{3} ; \dfrac{10}{3} \right)$
B. $(-\infty; 3)$
C. $\left( \dfrac{1}{3} ; \dfrac{10}{3} \right]$
D. $\left( -\infty ; \dfrac{10}{3} \right)$
Chọn A
Bất phương trình $\log_2(3x - 1) < 3 \Leftrightarrow 0 < 3x - 1 < 2^3$ hay $\dfrac{1}{3} < x < 3$.
Bất phương trình $\log_2(3x - 1) < 3 \Leftrightarrow 0 < 3x - 1 < 2^3$ hay $\dfrac{1}{3} < x < 3$.

Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A. 4
B. 2
C. 3
D. 1
Chọn B
A. $T = -1$
B. $T = -\dfrac{1}{2}$
C. $T = \dfrac{\sqrt{3}}{2}$
D. $T = -\dfrac{\sqrt{3}}{2}$
Chọn A
Ta có $T = \vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos(\vec{a}, \vec{b}) = 1 \cdot 1 \cdot \cos 120^0 = -\dfrac{1}{2}$.
Ta có $T = \vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos(\vec{a}, \vec{b}) = 1 \cdot 1 \cdot \cos 120^0 = -\dfrac{1}{2}$.
A. $A;C$
B. $S;C$
C. $B;C$
D. $M;C$
Chọn C
Do $SA \perp (ABC)$ nên $SA \perp BC$ mà $AB \perp BC$ nên $BC \perp (SAB)$. Chọn đáp án C.
Do $SA \perp (ABC)$ nên $SA \perp BC$ mà $AB \perp BC$ nên $BC \perp (SAB)$. Chọn đáp án C.
Phần 2. Thí sinh trả lời từ câu 1 đến câu 4.
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.Câu 1. Cho hàm đa thức $y = f(x)$ có đồ thị của hàm số $y = f'(x)$ là đường cong trong hình vẽ bên.

a) Hàm số $g(x) = f(x) - 2025x + 2024$ có đúng 2 điểm cực trị.
b) $\min f(x) = f(-1)$.
c) Hàm số $f(x)$ nghịch biến trên khoảng $(0;2)$.
d) Phương trình $f'( \cos x ) = 3$ có đúng 5 nghiệm thuộc $\left[0; \dfrac{5\pi}{2} \right]$.
Đáp án: SAI | ĐÚNG | SAI | ĐÚNG
a) Ta có $g'(x) = f'(x) - 2025$ nên $g'(x) = 0$ cho ta $f'(x) = 2025$. Dựa vào đồ thị của hàm số $f'(x)$ thì ta có phương trình $f'(x) = 2025$ có một nghiệm đơn $x = x_0$ nên $g'(x)$ đổi dấu qua nghiệm này. Vậy hàm số $g(x) = f(x) - 2025x + 2024$ có đúng một điểm cực trị. Chọn SAI.
b) Ta có bảng biến thiên của hàm số $y = f(x)$ như sau:

Dựa vào bảng biến thiên ta thấy $\min\limits_{\mathbb{R}} f(x) = f(-1)$. Chọn đáp án ĐÚNG.
c) Dựa vào bảng biến thiên ta cũng thấy hàm số $f(x)$ đồng biến trên $(0;2)$ nên ta chọn đáp án SAI.
d) Dựa vào đồ thị của hàm số $y = f'(x)$ thì ta có phương trình $f'(\cos x) = 3$ có các nghiệm thỏa mãn
$\cos x = a \in (-1;0)$, $\cos x = b \in (0;1)$ và $\cos x = c \in (1;2)$.
$ + \cos x = a \in (-1;0) \text{ cho 2 nghiệm } x \text{ phân biệt thuộc } \left[0; \frac{5\pi}{2} \right]. $
$ + \cos x = b \in (0;1) \text{ cho 3 nghiệm } x \text{ phân biệt thuộc } \left[0; \frac{5\pi}{2} \right]. $
$ + \cos x = c \in (2;+\infty) \text{ vô nghiệm}. $
Vậy phương trình $f'(\cos x) = 3$ có đúng 5 nghiệm thuộc $\left[0; \frac{5\pi}{2} \right]$. Chọn đáp án ĐÚNG.
a) Ta có $g'(x) = f'(x) - 2025$ nên $g'(x) = 0$ cho ta $f'(x) = 2025$. Dựa vào đồ thị của hàm số $f'(x)$ thì ta có phương trình $f'(x) = 2025$ có một nghiệm đơn $x = x_0$ nên $g'(x)$ đổi dấu qua nghiệm này. Vậy hàm số $g(x) = f(x) - 2025x + 2024$ có đúng một điểm cực trị. Chọn SAI.
b) Ta có bảng biến thiên của hàm số $y = f(x)$ như sau:

Dựa vào bảng biến thiên ta thấy $\min\limits_{\mathbb{R}} f(x) = f(-1)$. Chọn đáp án ĐÚNG.
c) Dựa vào bảng biến thiên ta cũng thấy hàm số $f(x)$ đồng biến trên $(0;2)$ nên ta chọn đáp án SAI.
d) Dựa vào đồ thị của hàm số $y = f'(x)$ thì ta có phương trình $f'(\cos x) = 3$ có các nghiệm thỏa mãn
$\cos x = a \in (-1;0)$, $\cos x = b \in (0;1)$ và $\cos x = c \in (1;2)$.
$ + \cos x = a \in (-1;0) \text{ cho 2 nghiệm } x \text{ phân biệt thuộc } \left[0; \frac{5\pi}{2} \right]. $
$ + \cos x = b \in (0;1) \text{ cho 3 nghiệm } x \text{ phân biệt thuộc } \left[0; \frac{5\pi}{2} \right]. $
$ + \cos x = c \in (2;+\infty) \text{ vô nghiệm}. $
Vậy phương trình $f'(\cos x) = 3$ có đúng 5 nghiệm thuộc $\left[0; \frac{5\pi}{2} \right]$. Chọn đáp án ĐÚNG.

Xét tính đúng sai của các mệnh đề sau:
a) Nếu gia tốc $a = 0{,}5 \, (m/s^2)$, thời gian tăng tốc $t_1$ bé hơn 21 giây.
b) Nếu gia tốc $b = 0{,}8 \, (m/s^2)$, thời gian giảm tốc $t_2$ lớn hơn 13 giây.
c) $\dfrac{1}{a} + \dfrac{1}{b} = \dfrac{5}{4}$.
d) Tổng quãng đường mà robot đã di chuyển từ $A$ đến $B$ là $550 \, m$.
Đáp án: ĐÚNG | SAI | SAI | ĐÚNG
Lần tăng tốc đầu tiên xe chuyển động với vận tốc $v(t) = at, \ (a > 0)$.
Đến khi xe đạt vận tốc 10m/s thì xe chuyển động hết $t_1 = \dfrac{10}{a} \ (s)$.
Lần giảm tốc, xe chuyển động với vận tốc $v_2 = 10 - bt, \ (b > 0)$.
Khi xe dừng lại thì xe chuyển động thêm được $10 - bt_2 = 0 \Rightarrow t_2 = \dfrac{10}{b} \ (s)$.
Tổng thời gian hành trình
Tổng thời gian: $t_1 + 40 + t_2 = 70 \Rightarrow \dfrac{10}{a} + \dfrac{10}{b} = 30 \Rightarrow \dfrac{1}{a} + \dfrac{1}{b} = 3$
a) Nếu gia tốc $a = 0{,}5 \left( \dfrac{m}{s^2} \right)$, thời gian tăng tốc $t_1 = \dfrac{10}{0{,}5} = 20$ giây $< 21$ giây. Đáp án: ĐÚNG.
b) Nếu gia tốc $b = 0{,}8 \left( \dfrac{m}{s^2} \right)$, thời gian giảm tốc $t_2 = \dfrac{10}{0{,}8} = 12{,}5$ giây $< 13$ giây. Đáp án: SAI.
c) Với $a > 0, \ b > 0$, ta có bất đẳng thức: $(a + b)\left( \dfrac{1}{a} + \dfrac{1}{b} \right) \ge 4$ mà $\dfrac{1}{a} + \dfrac{1}{b} = 3$ nên $a + b \ge \dfrac{4}{3}$
Do đó $a + b \le \dfrac{5}{4} \left( \dfrac{m}{s^2} \right)$ là một đáp án SAI.
d) Quãng đường tăng tốc: $S_1 = \int_0^{t_1} v(t)dt = \int_0^{t_1} at\,dt = \dfrac{1}{2}a(t_1)^2 = \dfrac{1}{2} \cdot \dfrac{100}{a} = \dfrac{50}{a} \ (m)$.
Quãng đường giảm tốc: $S_2 = \int_0^{t_2} (10 - bt)dt = 10t_2 - \dfrac{1}{2}bt_2^2$
Ta có $t_2 = \dfrac{10}{b} \Rightarrow S_2 = 10 \cdot \dfrac{10}{b} - \dfrac{1}{2}b \left( \dfrac{10}{b} \right)^2 = \dfrac{100}{b} - \dfrac{50}{b} = \dfrac{50}{b} \ (m)$
Quãng đường chuyển động đều: $10 \cdot 40 = 400 \ (m)$
Tổng quãng đường:
$\begin{array}{l} S = {S_1} + 400 + {S_2}\\ = \frac{{50}}{a} + 400 + \frac{{50}}{b}\\ = 50\left( {\frac{1}{a} + \frac{1}{b}} \right) + 400\\ = 150 + 400 = 550\;(m) \end{array}$
Đáp án: ĐÚNG.
Lần tăng tốc đầu tiên xe chuyển động với vận tốc $v(t) = at, \ (a > 0)$.
Đến khi xe đạt vận tốc 10m/s thì xe chuyển động hết $t_1 = \dfrac{10}{a} \ (s)$.
Lần giảm tốc, xe chuyển động với vận tốc $v_2 = 10 - bt, \ (b > 0)$.
Khi xe dừng lại thì xe chuyển động thêm được $10 - bt_2 = 0 \Rightarrow t_2 = \dfrac{10}{b} \ (s)$.
Tổng thời gian hành trình
Tổng thời gian: $t_1 + 40 + t_2 = 70 \Rightarrow \dfrac{10}{a} + \dfrac{10}{b} = 30 \Rightarrow \dfrac{1}{a} + \dfrac{1}{b} = 3$
a) Nếu gia tốc $a = 0{,}5 \left( \dfrac{m}{s^2} \right)$, thời gian tăng tốc $t_1 = \dfrac{10}{0{,}5} = 20$ giây $< 21$ giây. Đáp án: ĐÚNG.
b) Nếu gia tốc $b = 0{,}8 \left( \dfrac{m}{s^2} \right)$, thời gian giảm tốc $t_2 = \dfrac{10}{0{,}8} = 12{,}5$ giây $< 13$ giây. Đáp án: SAI.
c) Với $a > 0, \ b > 0$, ta có bất đẳng thức: $(a + b)\left( \dfrac{1}{a} + \dfrac{1}{b} \right) \ge 4$ mà $\dfrac{1}{a} + \dfrac{1}{b} = 3$ nên $a + b \ge \dfrac{4}{3}$
Do đó $a + b \le \dfrac{5}{4} \left( \dfrac{m}{s^2} \right)$ là một đáp án SAI.
d) Quãng đường tăng tốc: $S_1 = \int_0^{t_1} v(t)dt = \int_0^{t_1} at\,dt = \dfrac{1}{2}a(t_1)^2 = \dfrac{1}{2} \cdot \dfrac{100}{a} = \dfrac{50}{a} \ (m)$.
Quãng đường giảm tốc: $S_2 = \int_0^{t_2} (10 - bt)dt = 10t_2 - \dfrac{1}{2}bt_2^2$
Ta có $t_2 = \dfrac{10}{b} \Rightarrow S_2 = 10 \cdot \dfrac{10}{b} - \dfrac{1}{2}b \left( \dfrac{10}{b} \right)^2 = \dfrac{100}{b} - \dfrac{50}{b} = \dfrac{50}{b} \ (m)$
Quãng đường chuyển động đều: $10 \cdot 40 = 400 \ (m)$
Tổng quãng đường:
$\begin{array}{l} S = {S_1} + 400 + {S_2}\\ = \frac{{50}}{a} + 400 + \frac{{50}}{b}\\ = 50\left( {\frac{1}{a} + \frac{1}{b}} \right) + 400\\ = 150 + 400 = 550\;(m) \end{array}$
Đáp án: ĐÚNG.
- Trong tổng số 90 học sinh, có 50 học sinh nam và 40 học sinh nữ.
- Trong số 85 học sinh đạt huy chương, có 48 học sinh nam.
a) Xác suất chọn được một học sinh nữ là $\dfrac{4}{9}$.
b) Xác suất chọn được một học sinh nam và đạt huy chương là $\dfrac{7}{15}$.
c) Biết học sinh được chọn là nam, xác suất học sinh đó đạt huy chương là $\dfrac{24}{25}$.
d) Biết rằng học sinh được chọn đã đạt huy chương, xác suất học sinh đó là nữ là $\dfrac{37}{85}$.
Đáp án: ĐÚNG | SAI | ĐÚNG | ĐÚNG
N: Học sinh được chọn là nam
F: Học sinh được chọn là nữ
H: Học sinh được chọn đạt huy chương
K: Học sinh được chọn không đạt huy chương.
Tổng số học sinh (không gian mẫu): $n(\Omega) = 90$
Thông tin từ đề bài:
$n(N) = 50$; $n(F) = 40$; $n(H) = 85$
$n(N \cap H) = 48$ (Số học sinh nam đạt huy chương)
Từ đó suy ra:
$n(F \cap H) = n(H) - n(N \cap H) = 85 - 48 = 37$ (Số học sinh nữ đạt huy chương)
a) Xác suất chọn được học sinh nữ:
$P(F) = \dfrac{n(F)}{n(\Omega)} = \dfrac{40}{90} = \dfrac{4}{9}$. Đáp án: ĐÚNG.
b) Xác suất chọn được học sinh nam đạt huy chương:
$P(N \cap H) = \dfrac{n(N \cap H)}{n(\Omega)} = \dfrac{48}{90} = \dfrac{8}{15}$. Đáp án: SAI.
c) Xác suất học sinh đạt huy chương, biết rằng học sinh đó là nam:
$P(H \mid N) = \dfrac{P(N \cap H)}{P(N)} = \dfrac{8/15}{50/90} = \dfrac{24}{25}$. Đáp án: ĐÚNG.
d) Xác suất học sinh là nữ, biết rằng học sinh đó đã đạt huy chương:
$P(F \mid H) = \dfrac{P(F \cap H)}{P(H)} = \dfrac{37/90}{85/90} = \dfrac{37}{85}$. Đáp án: ĐÚNG.
N: Học sinh được chọn là nam
F: Học sinh được chọn là nữ
H: Học sinh được chọn đạt huy chương
K: Học sinh được chọn không đạt huy chương.
Tổng số học sinh (không gian mẫu): $n(\Omega) = 90$
Thông tin từ đề bài:
$n(N) = 50$; $n(F) = 40$; $n(H) = 85$
$n(N \cap H) = 48$ (Số học sinh nam đạt huy chương)
Từ đó suy ra:
$n(F \cap H) = n(H) - n(N \cap H) = 85 - 48 = 37$ (Số học sinh nữ đạt huy chương)
a) Xác suất chọn được học sinh nữ:
$P(F) = \dfrac{n(F)}{n(\Omega)} = \dfrac{40}{90} = \dfrac{4}{9}$. Đáp án: ĐÚNG.
b) Xác suất chọn được học sinh nam đạt huy chương:
$P(N \cap H) = \dfrac{n(N \cap H)}{n(\Omega)} = \dfrac{48}{90} = \dfrac{8}{15}$. Đáp án: SAI.
c) Xác suất học sinh đạt huy chương, biết rằng học sinh đó là nam:
$P(H \mid N) = \dfrac{P(N \cap H)}{P(N)} = \dfrac{8/15}{50/90} = \dfrac{24}{25}$. Đáp án: ĐÚNG.
d) Xác suất học sinh là nữ, biết rằng học sinh đó đã đạt huy chương:
$P(F \mid H) = \dfrac{P(F \cap H)}{P(H)} = \dfrac{37/90}{85/90} = \dfrac{37}{85}$. Đáp án: ĐÚNG.
a) Tọa độ điểm $C$ là $(3;3;0)$.
b) Trọng tâm của tam giác $PCD$ có tọa độ là $\left( \dfrac{2}{3}; \dfrac{5}{4};1 \right)$
c) Giá trị nhỏ nhất của biểu thức $\sqrt{KP^2 + KC^2 + KD^2}$ là $\dfrac{5}{2}$.
d) Góc giữa hai đường thẳng $AP$ và $BC'$ bằng $60^\circ$.
Đáp án: ĐÚNG | SAI | SAI | SAI
Ta có: $A(0;0;0), \ B(3;0;0),D(0;3;0),A'(0;0;3)$
Suy ra: $C(3;3;0),B'(3;0;3),D'(0;3;3),C'(3;3;3),P\left(3;\dfrac{-3}{2};3\right)$
a) Tọa độ điểm $C$ là $(3;3;0)$. Đáp án: ĐÚNG.
a) Trọng tâm G của tam giác $PCD$ có tọa độ là $\left(2;\dfrac{5}{2};1\right)$. Đáp án: SAI
b) $\left| {\overrightarrow {KP} + \overrightarrow {KC} + \overrightarrow {KD} } \right| = 3\overrightarrow {KG} $
Biểu thức $\overrightarrow{KP} + \overrightarrow{KC} + \overrightarrow{KD}$ đạt GTNN khi $KG$ nhỏ nhất. Suy ra $K$ là hình chiếu của $G$ lên $(Oxz)$
$\Rightarrow K(2;0;1). $ Suy ra $\left. \overrightarrow{KP} + \overrightarrow{KC} + \overrightarrow{KD} \right|_{\text{min}} = 3\overrightarrow{KG} = \dfrac{15}{2}$ Đáp án: SAI
c) $\overrightarrow{AP} = \left(3; \dfrac{3}{2};3 \right), \overrightarrow{BC'} = (0;3;3).$
$\begin{array}{l} \cos \left( {\overrightarrow {AP} ,\overrightarrow {BC'} } \right) = \left| {\cos \left( {\overrightarrow {AP} ,\overrightarrow {BC'} } \right)} \right|\\ = \frac{{\left| {\overrightarrow {AP} .\overrightarrow {BC'} } \right|}}{{|\overrightarrow {AP} |.|\overrightarrow {BC'} |}}\\ = \frac{{\left| {\frac{9}{2} + 9} \right|}}{{\sqrt {{3^2} + {{\left( {\frac{3}{2}} \right)}^2} + {3^2}} .\sqrt {{0^2} + {3^2} + {3^2}} }} = \frac{{\sqrt 2 }}{2} \end{array}$
Suy ra góc giữa hai đường thẳng $\overrightarrow{AP}$ và $\overrightarrow{BC'}$ bằng $45^0$. Đáp án: SAI
Ta có: $A(0;0;0), \ B(3;0;0),D(0;3;0),A'(0;0;3)$
Suy ra: $C(3;3;0),B'(3;0;3),D'(0;3;3),C'(3;3;3),P\left(3;\dfrac{-3}{2};3\right)$
a) Tọa độ điểm $C$ là $(3;3;0)$. Đáp án: ĐÚNG.
a) Trọng tâm G của tam giác $PCD$ có tọa độ là $\left(2;\dfrac{5}{2};1\right)$. Đáp án: SAI
b) $\left| {\overrightarrow {KP} + \overrightarrow {KC} + \overrightarrow {KD} } \right| = 3\overrightarrow {KG} $
Biểu thức $\overrightarrow{KP} + \overrightarrow{KC} + \overrightarrow{KD}$ đạt GTNN khi $KG$ nhỏ nhất. Suy ra $K$ là hình chiếu của $G$ lên $(Oxz)$
$\Rightarrow K(2;0;1). $ Suy ra $\left. \overrightarrow{KP} + \overrightarrow{KC} + \overrightarrow{KD} \right|_{\text{min}} = 3\overrightarrow{KG} = \dfrac{15}{2}$ Đáp án: SAI
c) $\overrightarrow{AP} = \left(3; \dfrac{3}{2};3 \right), \overrightarrow{BC'} = (0;3;3).$
$\begin{array}{l} \cos \left( {\overrightarrow {AP} ,\overrightarrow {BC'} } \right) = \left| {\cos \left( {\overrightarrow {AP} ,\overrightarrow {BC'} } \right)} \right|\\ = \frac{{\left| {\overrightarrow {AP} .\overrightarrow {BC'} } \right|}}{{|\overrightarrow {AP} |.|\overrightarrow {BC'} |}}\\ = \frac{{\left| {\frac{9}{2} + 9} \right|}}{{\sqrt {{3^2} + {{\left( {\frac{3}{2}} \right)}^2} + {3^2}} .\sqrt {{0^2} + {3^2} + {3^2}} }} = \frac{{\sqrt 2 }}{2} \end{array}$
Suy ra góc giữa hai đường thẳng $\overrightarrow{AP}$ và $\overrightarrow{BC'}$ bằng $45^0$. Đáp án: SAI
Phần 3. Thí sinh trả lời từ câu 1 đến câu 6.
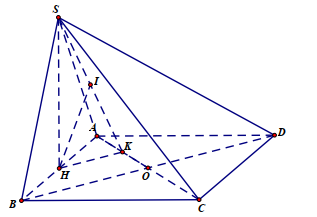
Câu 1. Cho hình chóp $S.ABCD$ có đáy là hình thoi cạnh $2\sqrt{5}$, tâm $O$ và $\angle ABC = 60^\circ$, mặt bên $SAB$ là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi $H$ là trung điểm cạnh $AB$. Tính bình phương khoảng cách từ $H$ đến mặt phẳng $(SAC)$.
Hạ $HK \perp AC$ ($K$ là trung điểm của $AO$) và hạ $HI \perp SK$ thì $HI$ là khoảng cách từ $H$ đến mặt phẳng $(SAC)$.
Tính $HI$.
Ta có : $BD = 2\sqrt{5}\sqrt{3} = 2\sqrt{15}$ nên $BO = \sqrt{15}$. Vậy $HK = \frac{1}{2}BO = \frac{\sqrt{15}}{2}$.
$SH$ là chiều cao trong tam giác đều $SAB$ nên $SH = \frac{AB\sqrt{3}}{2} = \sqrt{15}$.
Nên $\frac{1}{HI^2} - \frac{1}{HK^2} + \frac{1}{HS^2} = \frac{4}{15} - \frac{1}{15} = \frac{3}{15}$. Vậy $HI^2 = 3$.
Đáp án: 20
Tập xác định: $D = \mathbb{R} \backslash \{-1\}$
$y' = \frac{(2x-2)(x+1)-(x^2-2x-2)}{(x+1)^2} = \frac{x^2+2x}{(x+1)^2}$
$y' = 0 \Rightarrow {x^2} + 2x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {x = 0}\\ {x = - 2} \end{array}} \right.$
Hai điểm cực trị của đồ thị (C) là $A(-2;-6), B(0;-2)$
$\overrightarrow{AB} = (2,4) \Rightarrow AB^2 = 20$.
Tập xác định: $D = \mathbb{R} \backslash \{-1\}$
$y' = \frac{(2x-2)(x+1)-(x^2-2x-2)}{(x+1)^2} = \frac{x^2+2x}{(x+1)^2}$
$y' = 0 \Rightarrow {x^2} + 2x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {x = 0}\\ {x = - 2} \end{array}} \right.$
Hai điểm cực trị của đồ thị (C) là $A(-2;-6), B(0;-2)$
$\overrightarrow{AB} = (2,4) \Rightarrow AB^2 = 20$.
Đáp án: 8 (triệu đồng)
Theo gia thiết $p(x) = ax + b$.
Do đó, phương trình đường thẳng $p(x) = ax + b$ đi qua hai điểm $(1000;14)$ và $(1100;13,5)$.
Ta có hệ phương trình $\begin{cases} 14=1000a + b \\ 13,5=1100a + b \end{cases} \Leftrightarrow \begin{cases} a = -\frac{1}{200} \text{ (thỏa mãn)} \\ b = 19 \end{cases}$
Vậy $p(x) = -\frac{1}{200}x + 19$.
Doanh thu bán hàng của $x$ sản phẩm là $R(x) = x \cdot p(x) = x \cdot \left(-\frac{1}{200}x+19\right) = \frac{-x^2}{200}+19x$ (triệu đồng)
Do đó, hàm số thể hiện lợi nhuận thu được khi bán $x$ sản phẩm là
$P(x) = R(x) - C(x) = \frac{-x^2}{200}+19x - 12000 + 3x = \frac{-x^2}{200}+22x-12000$ (triệu đồng).
Để lợi nhuận là lớn nhất thì $P'(x)$ là lớn nhất.
Ta có: $P'(x) = \frac{-x}{100} + 22, P'(x) = 0 \Leftrightarrow x = 2200$.
Lập BBT, ta kết luận bán $2200$ cái điện thoại $A$ thì lợi nhuận là cao nhất. Vậy cửa hàng nên đặt giá bán là $p(2200) = 8$ (triệu đồng).
Theo gia thiết $p(x) = ax + b$.
Do đó, phương trình đường thẳng $p(x) = ax + b$ đi qua hai điểm $(1000;14)$ và $(1100;13,5)$.
Ta có hệ phương trình $\begin{cases} 14=1000a + b \\ 13,5=1100a + b \end{cases} \Leftrightarrow \begin{cases} a = -\frac{1}{200} \text{ (thỏa mãn)} \\ b = 19 \end{cases}$
Vậy $p(x) = -\frac{1}{200}x + 19$.
Doanh thu bán hàng của $x$ sản phẩm là $R(x) = x \cdot p(x) = x \cdot \left(-\frac{1}{200}x+19\right) = \frac{-x^2}{200}+19x$ (triệu đồng)
Do đó, hàm số thể hiện lợi nhuận thu được khi bán $x$ sản phẩm là
$P(x) = R(x) - C(x) = \frac{-x^2}{200}+19x - 12000 + 3x = \frac{-x^2}{200}+22x-12000$ (triệu đồng).
Để lợi nhuận là lớn nhất thì $P'(x)$ là lớn nhất.
Ta có: $P'(x) = \frac{-x}{100} + 22, P'(x) = 0 \Leftrightarrow x = 2200$.
Lập BBT, ta kết luận bán $2200$ cái điện thoại $A$ thì lợi nhuận là cao nhất. Vậy cửa hàng nên đặt giá bán là $p(2200) = 8$ (triệu đồng).
Đáp án: -5
Ta xem có một bạn áo $A$ ở kì I ngồi ở vị trí $(1,1)$ và sang kì II ngồi ở vị trí $(2,5)$.
Vậy số được gán cho bạn áo $A$ này là số: $(2+5)-(1+1)=5$.
Lúc này ta xem lớp học có đủ 36 bạn được xếp vào 36 vị trí. Chú ý tổng các số được đánh ở các bàn gồm hàng và cột có dạng $(i,j)$ với $i\in\{1;2;3;4\}$ và $j\in\{1;2;3;...;9\}$ nên $a_n\in\{1;2;3;4\}$ và $a_n\in\{1;2;3;...;9\}$.
Do đó tổng các số được gán cho 36 bạn là:
[(1 + 1) + (1 + 2) + ... + (1 + 9) + (2 + 1) + (2 + 2) + ... + (2 + 9) + ... + (4 + 1) + (4 + 2) + ... + (4 + 9)] - [(1 + 1) + (1 + 2) + ... + (1 + 9) + (2 + 1) + (2 + 2) + ... + (2 + 9) + ... + (4 + 1) + (4 + 2) + ... + (4 + 9)] = 0
Nên tổng số gán cho 35 bạn thực tế của lớp là: $0-5=-5$.
Ta xem có một bạn áo $A$ ở kì I ngồi ở vị trí $(1,1)$ và sang kì II ngồi ở vị trí $(2,5)$.
Vậy số được gán cho bạn áo $A$ này là số: $(2+5)-(1+1)=5$.
Lúc này ta xem lớp học có đủ 36 bạn được xếp vào 36 vị trí. Chú ý tổng các số được đánh ở các bàn gồm hàng và cột có dạng $(i,j)$ với $i\in\{1;2;3;4\}$ và $j\in\{1;2;3;...;9\}$ nên $a_n\in\{1;2;3;4\}$ và $a_n\in\{1;2;3;...;9\}$.
Do đó tổng các số được gán cho 36 bạn là:
[(1 + 1) + (1 + 2) + ... + (1 + 9) + (2 + 1) + (2 + 2) + ... + (2 + 9) + ... + (4 + 1) + (4 + 2) + ... + (4 + 9)] - [(1 + 1) + (1 + 2) + ... + (1 + 9) + (2 + 1) + (2 + 2) + ... + (2 + 9) + ... + (4 + 1) + (4 + 2) + ... + (4 + 9)] = 0
Nên tổng số gán cho 35 bạn thực tế của lớp là: $0-5=-5$.


Cách 1.
Gọi $x, \ y, \ z$ lần lượt là độ dài của các cạnh $AB, \ AD, \ AA'$.
Diện tích tất cả các mặt là $S_p = 2(xy + yz + zx) = 36 \Leftrightarrow xy + yz + zx = 18, \tag{1}$
Độ dài đường chéo $AC' = \sqrt{x^2 + y^2 + z^2} = 6 \Leftrightarrow x^2 + y^2 + z^2 = 36.$
Suy ra $(x + y + z)^2 = x^2 + y^2 + z^2 + 2(xy + yz + zx) = 72 \Leftrightarrow x + y + z = 6\sqrt{2}, \tag{2}$
Từ (2) ta có $y + z = 6\sqrt{2} - x$. Do đó, kết hợp với (1) ta được $ yz = 18 - x(y + z) = 18 - x\left(6\sqrt{2} - x\right) = x^2 - 6\sqrt{2}x + 18. $
Ta luôn có $(y + z)^2 \ge 4yz,\ \forall y, z$ nên $ (6\sqrt{2} - x)^2 \ge 4\left(x^2 - 6\sqrt{2}x + 18\right) \Leftrightarrow 3x^2 - 12\sqrt{2}x \le 0 \Leftrightarrow 0 \le x \le 4\sqrt{2}. $
Thể tích của khối hộp chữ nhật là $V = xyz = x\left(x^2 - 6\sqrt{2}x + 18\right) = x^3 - 6\sqrt{2}x^2 + 18x$.
Bài toán trở thành tìm giá trị lớn nhất của hàm số $f(x) = x^3 - 6\sqrt{2}x^2 + 18x$ trên đoạn $\left[0; 4\sqrt{2} \right]$.
Ta có $f'(x) = 3x^2 - 12\sqrt{2}x + 18$ và $f'(x) = 0 \Leftrightarrow \begin{cases} x = \sqrt{2} \in \left[0; 4\sqrt{2} \right] \\ x = 3\sqrt{2} \in \left[0; 4\sqrt{2} \right]. \end{cases}$
Ta tính được $f(0) = 0; \ f(4\sqrt{2}) = 8\sqrt{2}; \ f(\sqrt{2}) = 8\sqrt{2}; \ f(3\sqrt{2}) = 0$.
Với $x = \sqrt{2}$ thì $ \begin{cases} y + z = 5\sqrt{2} \\ yz = 8 \end{cases}. \text{Như thế } (x; y; z) \in \left\{ (\sqrt{2}; 4\sqrt{2}; \sqrt{2}), (\sqrt{2}; \sqrt{2}; 4\sqrt{2}) \right\}. $
Với $x = 4\sqrt{2}$ thì $ \begin{cases} y + z = 2\sqrt{2} \\ yz = 2 \end{cases}. \text{Như thế } (x; y; z) = (4\sqrt{2}; \sqrt{2}; \sqrt{2}). $
Vậy thể tích của khối hộp chữ nhật lớn nhất là $8\sqrt{2} \approx 11{,}3m^3$ khi $(x; y; z) = (\sqrt{2}; 4\sqrt{2}; \sqrt{2})$ và các hoán vị của nó.
Cách 2.
Gọi $x, \ y, \ z$ lần lượt là độ dài của các cạnh $AB, \ AD, \ AA'$.
Diện tích tất cả các mặt là $S_p = 2(xy + yz + zx) = 36 \Leftrightarrow xy + yz + zx = 18, \tag{1}$
Độ dài đường chéo $AC' = \sqrt{x^2 + y^2 + z^2} = 6 \Leftrightarrow x^2 + y^2 + z^2 = 36.$
Suy ra $(x + y + z)^2 = x^2 + y^2 + z^2 + 2(xy + yz + zx) = 72 \Leftrightarrow x + y + z = 6\sqrt{2}, \tag{2}$
Thể tích của khối hộp chữ nhật là $V = xyz, \tag{3}$
Từ (1), (2) và (3) suy ra $x, \ y, \ z$ là 3 nghiệm của phương trình
$X^3 - 6\sqrt{2}X^2 + 18X - V = 0 \Leftrightarrow V = X^3 - 6\sqrt{2}X^2 + 18X, \tag{4}$
Bảng biến thiên của hàm số $f(X) = X^3 - 6\sqrt{2}X^2 + 18X$ trên $(0; 6\sqrt{2})$ như sau

Dựa vào bảng biến thiên, giá trị lớn nhất của $V$ để phương trình $(4)$ có $3$ nghiệm (không cần phân biệt) trên khoảng $(0,6\sqrt{2})$ là $8\sqrt{2}$.
Vậy thể tích của khối hộp chữ nhật lớn nhất là $8\sqrt{2} = 11.3m^3$ khi $(x:y:z)=(\sqrt{2}:4\sqrt{2}:\sqrt{2})$ và các hoán vị của nó.


$\left\{ {\begin{array}{*{20}{l}} {\overrightarrow {AB} = ( - 4; - 2;4) = - 2(2;1; - 2)}\\ {\overrightarrow {{n_p}} = (2;1; - 2)} \end{array}} \right.$ $ \Rightarrow \overrightarrow {AB} ,\overrightarrow {{n_p}} $ cùng phương lên $\overrightarrow {AB} \bot (P),\;AB = 6$
$d\left( {A;(P)} \right) = \frac{{|2.3 + 5 - 2.( - 2) + 9|}}{{\sqrt {{2^2} + {1^2} + {{( - 2)}^2}} }} = 8{\rm{ }}$
và ${\rm{ }}d\left( {B;(P)} \right) = \frac{{|2.( - 1) + 3 - 2.2 + 9|}}{{\sqrt {{2^2} + {1^2} + {{( - 2)}^2}} }} = 2$
$AB \cap (P) = M$ suy ra M cố định
Do $(P)$ tiếp xúc với mặt cầu $(S)$ tại $C$ nên $MC \perp IC$ tại $C$
$ \Rightarrow MA \cdot MB = M{C^2},$ ta có ${\rm{ }}\left\{ {\begin{array}{*{20}{l}} {MA = d\left( {A;(P)} \right) = 8}\\ {MB = d\left( {B;(P)} \right) = 2} \end{array}} \right.$ $ \Leftrightarrow M{C^2} = 16$
$ \Leftrightarrow MC = 4$
Vậy C thuộc đường tròn tâm M bán kính r = MC = 4
Ta có: $\overrightarrow {AB} :\left\{ {\begin{array}{*{20}{l}} {x = 3 + 2t}\\ {y = 5 + t}\\ {z = - 2 - 2t} \end{array}} \right.,\quad $ $M = AB \cap (P) \Rightarrow M\left( {\frac{{ - 7}}{3},\frac{7}{3},\frac{{10}}{3}} \right)$
Gọi $H$ là hình chiếu của $O$ lên mặt phẳng $(P) \Rightarrow d\left(O, (P)\right) = 3$, $OH :$ $ \begin{cases} x = 2t \\ y = t \\ z = -2t \end{cases} $
$H = OH \cap (P) \Leftrightarrow H( - 2; - 1;2),\;$ $HM = \sqrt {13} < 4{\rm{ }}$ nên H nằm trong đường tròn tâm M bán kính $r = MC = 4.{\rm{ }}$
${\rm{Suy ra }}OC = \sqrt {O{H^2} + H{C^2}} = \sqrt {9 + H{C^2}} $
=> OC đạt min hoặc max <=> HC đạt min hoặc max
$\left\{ {\begin{array}{*{20}{l}} {H{C_{{\rm{min}}}} = |HM - r| = 4 - \sqrt {13} }\\ {H{C_{{\rm{max}}}} = HM + r = 4 + \sqrt {13} } \end{array}} \right.$ $ \Rightarrow \left\{ {\begin{array}{*{20}{l}} {O{C_{{\rm{min}}}} = \sqrt {9 + {{(4 - \sqrt {13} )}^2}} = {m_2}}\\ {O{C_{{\rm{max}}}} = \sqrt {9 + {{(4 + \sqrt {13} )}^2}} = {m_1}} \end{array}} \right.$
Vậy $m_1^2 + m_2^2 = 76$
