Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
Câu 1. Trong không gian $Oxyz$, cho mặt phẳng $\left( P \right):2x-y+3z-4=0$. Một vectơ pháp tuyến của mặt phẳng $\left( P \right)$ có tọa độ là
A.$\left( 3;-1;2 \right)$. B.$\left( 2;-1;3 \right)$ .
C. $\left( -1;2;3 \right)$.
D. $\left( 2;1;3 \right)$.
Một vectơ pháp tuyến của mặt phẳng $\left( P \right)$ có tọa độ là $\left( 2;-1;3 \right)$.
A.$x=\frac{1}{2}$.
B. $y=2$ .
C. $x=-2$.
D. $y=-2$.
Tiệm cận đứng của đồ thị hàm số là đường thẳng có phương trình $x=-2$.
A.$\frac{x+1}{1}=\frac{y+3}{-5}=\frac{z-2}{1}$. B.$\frac{x-1}{1}=\frac{y-3}{3}=\frac{z+2}{-2}$.
C. $\frac{x-2}{1}=\frac{y+2}{-5}=\frac{z+1}{1}$.
D. $\frac{x+2}{1}=\frac{y-2}{-5}=\frac{z-1}{1}$.
Vectơ chỉ phương của đường thẳng $AB$ là $\overrightarrow{u}=\overrightarrow{AB}=\left( 1;-5;1 \right)$.
Phương trình đường thẳng $AB$ là $\frac{x-2}{1}=\frac{y+2}{-5}=\frac{z+1}{1}$.
Phương trình đường thẳng $AB$ là $\frac{x-2}{1}=\frac{y+2}{-5}=\frac{z+1}{1}$.
A. $\left[ 3;+\infty \right)$.
B. $\left( -\infty ;-3 \right]$.
C. $\left[ -3;+\infty \right)$.
D. $\left( -3;+\infty \right)$.
Ta có
$\begin{array}{l} {\left( {\frac{1}{2}} \right)^{2x + 3}} \le 8\,\\ \Leftrightarrow \,{2^{ - 2x - 3}} \le {2^3}\,\,\\ \Leftrightarrow - 2x - 3 \le 3\\ \Leftrightarrow x \ge - 3 \end{array}$.
Vậy tập nghiệm của bất phương trình là $S=\left[ -3;+\infty \right)$.
$\begin{array}{l} {\left( {\frac{1}{2}} \right)^{2x + 3}} \le 8\,\\ \Leftrightarrow \,{2^{ - 2x - 3}} \le {2^3}\,\,\\ \Leftrightarrow - 2x - 3 \le 3\\ \Leftrightarrow x \ge - 3 \end{array}$.
Vậy tập nghiệm của bất phương trình là $S=\left[ -3;+\infty \right)$.

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là :
A. $25$.
B. $20$.
C. $30$.
D. $15$.
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là : $90-65=25$.
A. $F\left( x \right)=-{{e}^{x}}-2\cos x+23$.
B. $F\left( x \right)={{e}^{x}}-2\cos x+21$.
C. $F\left( x \right)={{e}^{x}}+2\cos x+17$.
D. $F\left( x \right)={{e}^{x}}+2\sin x+19$.
$\begin{array}{l} F\left( x \right) = \int {f\left( x \right)dx} \\ = \int {\left( {{e^x} + 2\sin x} \right)} dx\\ = {e^x} - 2\cos x + C \end{array}$
Mà $F\left( 0 \right)=20\Leftrightarrow {{e}^{0}}-2\cos 0+C=20\Leftrightarrow C=21$ .
Vậy $F\left( x \right)={{e}^{x}}-2\cos x+21$.
Mà $F\left( 0 \right)=20\Leftrightarrow {{e}^{0}}-2\cos 0+C=20\Leftrightarrow C=21$ .
Vậy $F\left( x \right)={{e}^{x}}-2\cos x+21$.
A. $40500$.
B. $121500$.
C. $1965$.
D. $33,75$.
Ta có thể tích của khối chóp là $V=\frac{1}{3}.2025.60=40500$.

Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng bao nhiêu?
A. $3$.
B. $2$.
C. $-5$.
D. $-3$.
Từ bảng biến thiên ta có ${{y}_{C\text{D}}}=2$; ${{y}_{CT}}=-5$.
Tổng giá trị cực đại và giá trị cực tiểu là : $2+\left( -5 \right)=-3$.
Tổng giá trị cực đại và giá trị cực tiểu là : $2+\left( -5 \right)=-3$.
A. $x=2$.
B. $x=5$.
C. $x=14$.
D. $x=41$.
Ta có:
$\begin{array}{l} {\log _3}\left( {2x - 1} \right) = 3\\ \Leftrightarrow 2x - 1 = {3^3}\\ \Leftrightarrow 2x = 28\\ \Leftrightarrow x = 14 \end{array}$
Vậy nghiệm của phương trình là $x=14$.
$\begin{array}{l} {\log _3}\left( {2x - 1} \right) = 3\\ \Leftrightarrow 2x - 1 = {3^3}\\ \Leftrightarrow 2x = 28\\ \Leftrightarrow x = 14 \end{array}$
Vậy nghiệm của phương trình là $x=14$.
A. $1$.
B. $\frac{2}{3}$.
C. $\frac{1}{2}$.
D. $\frac{4}{3}$.
Ta có diện tích hình phẳng giới hạn bởi đồ thị hàm số $y={{x}^{2}}-2x,\,y=-2{{x}^{2}}+2x$ và hai đường thẳng $x=0,\,x=1$ là $\int\limits_{0}^{1}{\left| \left( {{x}^{2}}-2x \right)-\left( -2{{x}^{2}}+2x \right) \right|}\,\text{d}x=1$.
A. $10$.
B. $14$.
C. $11$.
D. $8$.
Ta có ${{u}_{9}}={{u}_{1}}+8d\Leftrightarrow 23=-1+8d\Leftrightarrow d=3$ suy ra ${{u}_{5}}={{u}_{1}}+4d=-1+4.3=11$ .
A. $\sqrt{2}$.
B. $\sqrt{3}$.
C. $1$.
D. $2$.
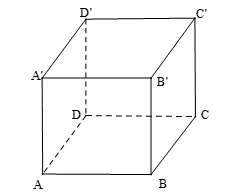
Ta có $\left| \overrightarrow{AB}+\overrightarrow{C{C}'} \right|=\left| \overrightarrow{AB}+\overrightarrow{A{A}'} \right|=\left| \overrightarrow{A{B}'} \right|=A{B}'=\sqrt{2}$.
Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S).PHẦN II. Câu trắc nghiệm đúng sai.
Câu 1. Trong không gian $Oxyz$, cho điểm $M\left( 3;1;9 \right)$, đường thẳng $d:\left\{ {\begin{array}{*{20}{l}} {x = t}\\ {y = - 1 - t}\\ {z = 2 + 2t} \end{array}} \right.$ và mặt phẳng$\left( \alpha \right):x+y-z+3=0$.
a) Điểm $A$ có tọa độ dạng $A\left( t;-1-t;2+2t \right)$ với $t\in \mathbb{R}$ thì $A$ thuộc đường thẳng $d$.
b) Một vectơ pháp tuyến của mặt phẳng $(\alpha )$ là $\vec{n}=\left( 1;1;-1 \right)$.
c) Điểm $M$ thuộc đường thẳng $d$.
d) Đường thẳng $\Delta $ đi qua $M$, cắt đường thẳng $d$ và song song với mặt phẳng $\left( \alpha \right)$ có phương trình là $\frac{x-1}{2}=\frac{y+2}{3}=\frac{z-4}{5}$.
a) Đúng.
Vì $d:\left\{ {\begin{array}{*{20}{l}} {x = t}\\ {y = - 1 - t}\\ {z = 2 + 2t} \end{array}} \right.$ nên khi $A\left( t;-1-t;2+2t \right)$ thì $A$ thuộc đường thẳng $d$.
b) Đúng.
Một vectơ pháp tuyến của mặt phẳng $(\alpha )$ là $\vec{n}=\left( 1;1;-1 \right)$.
c) Sai.
Xét $\left\{ \begin{array}{*{35}{l}} 3=t \\ 1=-1-t \\ 9=2+2t \\ \end{array} \right.$ $\Leftrightarrow $ $\left\{ \begin{array}{*{35}{l}} t=3 \\ t=-2 \\ t=\frac{7}{2} \\ \end{array} \right.$ (Vô lý).
Vậy điểm $M$ không thuộc đường thẳng $d$.
d) Đúng.
Gọi đường thẳng $\Delta $ cắt đường thẳng $d$ tại $N$.
Suy ra $N\left( t;-1-t;2+2t \right)$
Ta có : $\overrightarrow{{{u}_{\Delta }}}=\overrightarrow{MN}=\left( t-3;-t-2;2t-7 \right)$ và ${{\vec{n}}_{\left( \alpha \right)}}=\left( 1;1;-1 \right)$.
Vì đường thẳng $\Delta $ song song với mặt phẳng $\left( \alpha \right)$ nên $\overrightarrow{{{u}_{\Delta }}}\bot {{\vec{n}}_{\left( \alpha \right)}}$.
Suy ra
$1.\left( t-3 \right)+1.\left( -t-2 \right)-1.\left( 2t-7 \right)=0$ $\Leftrightarrow $ $-2t+2=0$ $\Leftrightarrow $ $t=1$.
Suy ra $\overrightarrow{{{u}_{\Delta }}}=\left( -2;-3;-5 \right)$ và $N\left( 1;-2;4 \right)$.
Khi đó : $\Delta :\frac{x-1}{2}=\frac{y+2}{3}=\frac{z-4}{5}$.
Vì $d:\left\{ {\begin{array}{*{20}{l}} {x = t}\\ {y = - 1 - t}\\ {z = 2 + 2t} \end{array}} \right.$ nên khi $A\left( t;-1-t;2+2t \right)$ thì $A$ thuộc đường thẳng $d$.
b) Đúng.
Một vectơ pháp tuyến của mặt phẳng $(\alpha )$ là $\vec{n}=\left( 1;1;-1 \right)$.
c) Sai.
Xét $\left\{ \begin{array}{*{35}{l}} 3=t \\ 1=-1-t \\ 9=2+2t \\ \end{array} \right.$ $\Leftrightarrow $ $\left\{ \begin{array}{*{35}{l}} t=3 \\ t=-2 \\ t=\frac{7}{2} \\ \end{array} \right.$ (Vô lý).
Vậy điểm $M$ không thuộc đường thẳng $d$.
d) Đúng.
Gọi đường thẳng $\Delta $ cắt đường thẳng $d$ tại $N$.
Suy ra $N\left( t;-1-t;2+2t \right)$
Ta có : $\overrightarrow{{{u}_{\Delta }}}=\overrightarrow{MN}=\left( t-3;-t-2;2t-7 \right)$ và ${{\vec{n}}_{\left( \alpha \right)}}=\left( 1;1;-1 \right)$.
Vì đường thẳng $\Delta $ song song với mặt phẳng $\left( \alpha \right)$ nên $\overrightarrow{{{u}_{\Delta }}}\bot {{\vec{n}}_{\left( \alpha \right)}}$.
Suy ra
$1.\left( t-3 \right)+1.\left( -t-2 \right)-1.\left( 2t-7 \right)=0$ $\Leftrightarrow $ $-2t+2=0$ $\Leftrightarrow $ $t=1$.
Suy ra $\overrightarrow{{{u}_{\Delta }}}=\left( -2;-3;-5 \right)$ và $N\left( 1;-2;4 \right)$.
Khi đó : $\Delta :\frac{x-1}{2}=\frac{y+2}{3}=\frac{z-4}{5}$.
a) Lợi nhuận mà nhà máy A thu được khi bán $x$ (tấn) sản phẩm $(0\le x\le 100)$ cho nhà máy B là $H\left( x \right)=-0,001{{x}^{3}}+15x-100$.
b) Chi phí để nhà máy A sản xuất $10$ tấn sản phẩm trong một tháng là 400 triệu đồng.
c) Số tiền nhà máy A thu được khi bán $10$ tấn sản phẩm cho nhà máy B là $600$ triệu đồng.
d) Nhà máy A bán cho nhà máy B khoảng $70,7$ tấn sản phẩm mỗi tháng thì thu được lợi nhuận lớn nhất.
a) Đúng.
Lợi nhuận mà nhà máy A thu được khi bán $x$ (tấn) sản phẩm $(0\le x\le 100)$ cho nhà máy B là:
$\begin{array}{l} H\left( x \right) = x.P\left( x \right) - C\left( x \right)\\ = x.\left( {45 - 0,001{x^2}} \right) - \left( {100 + 30x} \right)\\ = - 0,001{x^3} + 15x - 100 \end{array}$.
b) Đúng.
Chi phí để nhà máy A sản xuất $10$ tấn sản phẩm trong một tháng là:
$C\left( 10 \right)=100+30.10=400$ (triệu đồng).
c) Sai.
Số tiền nhà máy A thu được khi bán $10$ tấn sản phẩm cho nhà máy B là:
$10P\left( 10 \right)=10.\left( 45-{{0,001.10}^{2}} \right)=449$ (triệu đồng)
d) Đúng.
Xét hàm số $H\left( x \right)=-0,001{{x}^{3}}+15x-100$ trên $\left[ 0;100 \right]$.
+ ${H}'(x)=-0,003{{x}^{2}}+15$
+ ${H}'(x)=0$ $\Leftrightarrow $ $-0,003{{x}^{2}}+15=0$ $\Leftrightarrow $${{x}^{2}}=5000$ $\Rightarrow $ $x=50\sqrt{2}\approx 70,7\in \left[ 0;100 \right]$
+ $\left\{ \begin{align} & H\left( 0 \right)=-100 \\ & H\left( 50\sqrt{2} \right)\approx 607,11 \\ & H\left( 100 \right)=400 \\ \end{align} \right.$
Vậy nhà máy A bán cho nhà máy B khoảng $70,7$ tấn sản phẩm mỗi tháng thì thu được lợi nhuận lớn nhất bằng $607,11$ (triệu đồng).
Lợi nhuận mà nhà máy A thu được khi bán $x$ (tấn) sản phẩm $(0\le x\le 100)$ cho nhà máy B là:
$\begin{array}{l} H\left( x \right) = x.P\left( x \right) - C\left( x \right)\\ = x.\left( {45 - 0,001{x^2}} \right) - \left( {100 + 30x} \right)\\ = - 0,001{x^3} + 15x - 100 \end{array}$.
b) Đúng.
Chi phí để nhà máy A sản xuất $10$ tấn sản phẩm trong một tháng là:
$C\left( 10 \right)=100+30.10=400$ (triệu đồng).
c) Sai.
Số tiền nhà máy A thu được khi bán $10$ tấn sản phẩm cho nhà máy B là:
$10P\left( 10 \right)=10.\left( 45-{{0,001.10}^{2}} \right)=449$ (triệu đồng)
d) Đúng.
Xét hàm số $H\left( x \right)=-0,001{{x}^{3}}+15x-100$ trên $\left[ 0;100 \right]$.
+ ${H}'(x)=-0,003{{x}^{2}}+15$
+ ${H}'(x)=0$ $\Leftrightarrow $ $-0,003{{x}^{2}}+15=0$ $\Leftrightarrow $${{x}^{2}}=5000$ $\Rightarrow $ $x=50\sqrt{2}\approx 70,7\in \left[ 0;100 \right]$
+ $\left\{ \begin{align} & H\left( 0 \right)=-100 \\ & H\left( 50\sqrt{2} \right)\approx 607,11 \\ & H\left( 100 \right)=400 \\ \end{align} \right.$
Vậy nhà máy A bán cho nhà máy B khoảng $70,7$ tấn sản phẩm mỗi tháng thì thu được lợi nhuận lớn nhất bằng $607,11$ (triệu đồng).
a) Đạo hàm của hàm số đã cho nhận giá trị âm trên các khoảng $\left( -2;0 \right)\cup \left( 0;2 \right)$ và nhận giá trị dương trên các khoảng $\left( -\infty ;-2 \right)\cup \left( 2;+\infty \right)$.
b) Đạo hàm của hàm số đã cho là ${y}'=1-\frac{4}{{{x}^{2}}}$.
c) Bảng biến thiên của hàm số đã cho là
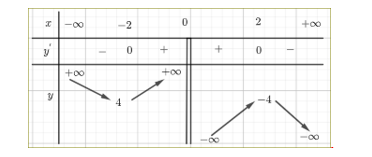
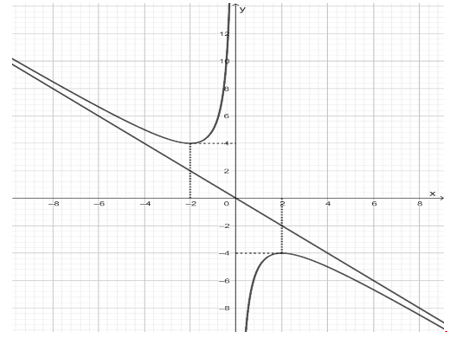
d) Đồ thị của hàm số đã cho là
Tập xác định của hàm số $D=\mathbb{R}\backslash \left\{ 0 \right\}$.
Ta có $y=x+\frac{4}{x}\Rightarrow {y}'=1-\frac{4}{{{x}^{2}}}=\frac{{{x}^{2}}-4}{{{x}^{2}}}$.
+ ${y}'=0\Rightarrow {{x}^{2}}-4=0\Leftrightarrow x=\pm 2$.
Ta có bảng biến thiên
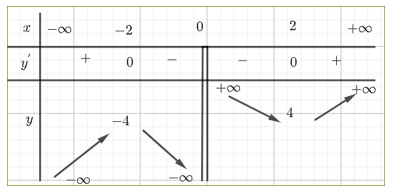
a) Đúng.
b) Đúng.
c) Sai.
d) Sai.
Đồ thị hàm số đã cho là
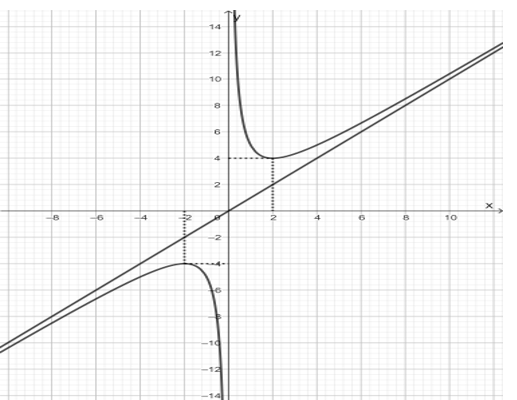
Ta có $y=x+\frac{4}{x}\Rightarrow {y}'=1-\frac{4}{{{x}^{2}}}=\frac{{{x}^{2}}-4}{{{x}^{2}}}$.
+ ${y}'=0\Rightarrow {{x}^{2}}-4=0\Leftrightarrow x=\pm 2$.
Ta có bảng biến thiên

a) Đúng.
b) Đúng.
c) Sai.
d) Sai.
Đồ thị hàm số đã cho là

a) Biết công ty không thắng thầu dự án 1, xác suất để công ty thắng thầu dự án 2 là $0,8$.
b) $A$ và $B$ là hai biến cố độc lập.
c) Biết công ty thắng thầu dư án 1, xác suất để công ty thắng thầu dự án 2 là $0,4$.
d) Xác suất để công ty thắng thầu đúng một dự án là $0,3$.
a) Sai. Ta có $P\left( {\left. B \right|\overline A } \right) = \frac{{P\left( {B\overline A } \right)}}{{p\left( {\overline A } \right)}}$ $ = \frac{{P\left( B \right) - P(BA)}}{{P\left( {\overline A } \right)}}$ $ = \frac{{0,6 - 0,4}}{{0,5}} = 0,4$
b) Sai. $P\left( AB \right)=0,4\ne 0,5.0,6=P\left( A \right).P\left( B \right)$ nên $A$ và $B$ là hai biến cố không độc lập.
c) Sai. Ta có $P\left( \left. B \right|A \right)=\frac{P\left( BA \right)}{p\left( A \right)}=\frac{0,4}{0,5}=0,8$.
d) Đúng. Xác suất để công ty thắng thầu đúng một dự án là
$\begin{array}{l} P\left( {A\overline B } \right) + P\left( {B\overline A } \right)\\ = P\left( A \right) - P\left( {AB} \right) + P\left( B \right) - P\left( {AB} \right)\\ = 0,5 - 0,4 + 0,6 - 0,4 = 0,3 \end{array}$.
b) Sai. $P\left( AB \right)=0,4\ne 0,5.0,6=P\left( A \right).P\left( B \right)$ nên $A$ và $B$ là hai biến cố không độc lập.
c) Sai. Ta có $P\left( \left. B \right|A \right)=\frac{P\left( BA \right)}{p\left( A \right)}=\frac{0,4}{0,5}=0,8$.
d) Đúng. Xác suất để công ty thắng thầu đúng một dự án là
$\begin{array}{l} P\left( {A\overline B } \right) + P\left( {B\overline A } \right)\\ = P\left( A \right) - P\left( {AB} \right) + P\left( B \right) - P\left( {AB} \right)\\ = 0,5 - 0,4 + 0,6 - 0,4 = 0,3 \end{array}$.
Thí sinh trả lời từ câu 1 đến câu 4.PHẦN III. Câu trắc nghiệm trả lời ngắn.
Câu 1. Cho tứ diện $ABCD$ có tất cả các cạnh bằng nhau và bằng $a$. Tính côsin của góc giữa đường thẳng $AB$ và mặt phẳng $\left( BCD \right)$( làm tròn kết quả đến chữ số thập phân thứ 2).
:
Đáp số: 0,58
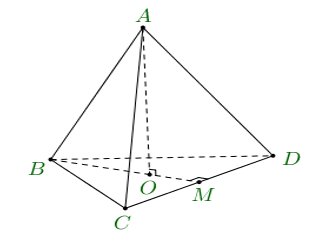
Ta có $AB=a,\,a>0$. Gọi $O$ là tâm của tam giác đều $BCD$, gọi $M$ là trung điểm của $CD$.
Vì $ABCD$ là tứ diện đều nên $AO\bot \left( BCD \right)$.
$\Rightarrow $ Hình chiếu của $AB$ lên mp$\left( BCD \right)$ là $OB$$\Rightarrow $ Góc giữa $AB$ và mp$\left( BCD \right)$ là góc $\widehat{ABO}$.
Ta có $AB=a,BM=\frac{a\sqrt{3}}{2},BO=\frac{2}{3}BM=\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}$.
Xét $\Delta ABO$ vuông tại $O$: $\cos \widehat{ABO}=\frac{OB}{AB}=\frac{\frac{a\sqrt{3}}{3}}{a}=\frac{\sqrt{3}}{3}\approx 0,58$ .
Đáp số: 0,58

Ta có $AB=a,\,a>0$. Gọi $O$ là tâm của tam giác đều $BCD$, gọi $M$ là trung điểm của $CD$.
Vì $ABCD$ là tứ diện đều nên $AO\bot \left( BCD \right)$.
$\Rightarrow $ Hình chiếu của $AB$ lên mp$\left( BCD \right)$ là $OB$$\Rightarrow $ Góc giữa $AB$ và mp$\left( BCD \right)$ là góc $\widehat{ABO}$.
Ta có $AB=a,BM=\frac{a\sqrt{3}}{2},BO=\frac{2}{3}BM=\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}$.
Xét $\Delta ABO$ vuông tại $O$: $\cos \widehat{ABO}=\frac{OB}{AB}=\frac{\frac{a\sqrt{3}}{3}}{a}=\frac{\sqrt{3}}{3}\approx 0,58$ .
:
Đáp số: 0,45
Gọi $\mathbb{R}\backslash \left\{ \pm 1 \right\}$ là biến cố $2$viên bi lấy ra ở hộp thứ hai có cùng màu
Gọi $3$là biến cố $3$viên bi lấy ra ở hộp thứ nhất có cùng màu.
Ta có
$P\left( B \right)=\frac{C_{5}^{3}}{C_{6}^{3}}=\frac{1}{2},\,\,P\left( {\bar{B}} \right)=\frac{1}{2}$ (vì hộp thứ nhất chỉ có 5 bi xanh và 1 bi đỏ).
Xác suất để $2$viên bi được chọn từ hộp thứ hai có cùng màu, biết $3$viên bi lấy ra ở hộp thứ nhất có cùng màu là
$P\left( A|B \right)=\frac{C_{3}^{2}+C_{4}^{2}}{C_{7}^{2}}=\frac{3}{7}$ (vì sau khi lấy 3 viên bi màu xanh từ hộp thứ nhất sang thì hộp thứ hai có 3 bi xanh và 4 bi đỏ).
Xác suất để $2$viên bi được chọn từ hộp thứ hai có cùng màu, biết $3$viên bi lấy ra ở hộp thứ nhất khác màu là
$P\left( A|\overline{B} \right)=\frac{C_{2}^{2}+C_{5}^{2}}{C_{7}^{2}}=\frac{11}{21}$ (vì sau khi lấy 2 viên bi màu xanh và 1 viên bi đỏ từ hộp thứ nhất sang thì hộp thứ hai có 2 bi xanh và 5 bi đỏ).
Áp dụng công thức xác suất toàn phần ta có
$\begin{array}{l} P\left( A \right) = P\left( B \right)P\left( {A|B} \right) + P\left( {\overline B } \right)P\left( {A|\overline B } \right)\\ = \frac{1}{2}.\frac{3}{7} + \frac{1}{2}.\frac{{11}}{{21}} = \frac{{10}}{{21}} \end{array}$.
Theo công thức Bayes, ta có: $P\left( B|A \right)=\frac{P\left( B \right)\,.\,P\left( A|B \right)}{P\left( A \right)}=\frac{\frac{1}{2}\,.\,\frac{3}{7}}{\frac{10}{21}}=\frac{9}{20}=0,45$.
Đáp số: 0,45
Gọi $\mathbb{R}\backslash \left\{ \pm 1 \right\}$ là biến cố $2$viên bi lấy ra ở hộp thứ hai có cùng màu
Gọi $3$là biến cố $3$viên bi lấy ra ở hộp thứ nhất có cùng màu.
Ta có
$P\left( B \right)=\frac{C_{5}^{3}}{C_{6}^{3}}=\frac{1}{2},\,\,P\left( {\bar{B}} \right)=\frac{1}{2}$ (vì hộp thứ nhất chỉ có 5 bi xanh và 1 bi đỏ).
Xác suất để $2$viên bi được chọn từ hộp thứ hai có cùng màu, biết $3$viên bi lấy ra ở hộp thứ nhất có cùng màu là
$P\left( A|B \right)=\frac{C_{3}^{2}+C_{4}^{2}}{C_{7}^{2}}=\frac{3}{7}$ (vì sau khi lấy 3 viên bi màu xanh từ hộp thứ nhất sang thì hộp thứ hai có 3 bi xanh và 4 bi đỏ).
Xác suất để $2$viên bi được chọn từ hộp thứ hai có cùng màu, biết $3$viên bi lấy ra ở hộp thứ nhất khác màu là
$P\left( A|\overline{B} \right)=\frac{C_{2}^{2}+C_{5}^{2}}{C_{7}^{2}}=\frac{11}{21}$ (vì sau khi lấy 2 viên bi màu xanh và 1 viên bi đỏ từ hộp thứ nhất sang thì hộp thứ hai có 2 bi xanh và 5 bi đỏ).
Áp dụng công thức xác suất toàn phần ta có
$\begin{array}{l} P\left( A \right) = P\left( B \right)P\left( {A|B} \right) + P\left( {\overline B } \right)P\left( {A|\overline B } \right)\\ = \frac{1}{2}.\frac{3}{7} + \frac{1}{2}.\frac{{11}}{{21}} = \frac{{10}}{{21}} \end{array}$.
Theo công thức Bayes, ta có: $P\left( B|A \right)=\frac{P\left( B \right)\,.\,P\left( A|B \right)}{P\left( A \right)}=\frac{\frac{1}{2}\,.\,\frac{3}{7}}{\frac{10}{21}}=\frac{9}{20}=0,45$.
Đáp số: 20
Giả sử lãi suất hàng tháng là $r$
Anh Bình gửi 1 triệu đồng thì số tiền anh Bình được lĩnh sau khi gửi tháng đầu tiên là $1.000.000\left( 1+r \right)$
Tiếp tục cuối tháng anh Bình gửi 1 triệu đồng thì số tiền anh Bình được lĩnh sau khi gửi tháng thứ hai là
$\begin{array}{l} \left[ {1.000.000\left( {1 + r} \right) + 1.000.000} \right]\left( {1 + r} \right)\\ = 1.000.000{\left( {1 + r} \right)^2} + 1.000.000\left( {1 + r} \right)\\ = 1.000.000\left[ {{{\left( {1 + r} \right)}^2} + \left( {1 + r} \right)} \right] \end{array}$
Tiếp tục như vậy, sau $n$ tháng thì số tiền anh Bình có được là:
$\begin{array}{l} 1.000.000\left[ {{{\left( {1 + r} \right)}^n} + {{\left( {1 + r} \right)}^{n - 1}} + ... + \left( {1 + r} \right)} \right]\\ = 1.000.000\frac{{\left( {1 + r} \right)\left( {{{\left( {1 + r} \right)}^n} - 1} \right)}}{r} \end{array}$
Để có được 21 triệu đồng để mua được một chiếc xe máy thì cần tìm sao cho
$\begin{array}{l} 1.000.000\frac{{\left( {1 + r} \right)\left( {{{\left( {1 + r} \right)}^n} - 1} \right)}}{r} \ge 21.000.000\\ \Leftrightarrow \frac{{\left( {1 + r} \right)\left( {{{\left( {1 + r} \right)}^n} - 1} \right)}}{r} \ge 21 \end{array}$
Lãi suất $8%$/năm tương ứng với lãi suất $\frac{2}{3}%$/tháng.
Nên
$\begin{array}{l} \frac{{\left( {1 + \frac{2}{3}\% } \right)\left( {{{\left( {1 + \frac{2}{3}\% } \right)}^n} - 1} \right)}}{{\frac{2}{3}\% }} \ge 21\\ \Leftrightarrow n \ge {\log _{1 + \frac{2}{3}\% }}\left( {\frac{{21.\frac{2}{3}\% }}{{1 + \frac{2}{3}\% }} + 1} \right) \Leftrightarrow n \ge 19,59 \end{array}$
Nghía là anh Bình cần gửi tối thiểu 20 tháng thì sẽ đủ tiền để mua xe máy.
Giả sử lãi suất hàng tháng là $r$
Anh Bình gửi 1 triệu đồng thì số tiền anh Bình được lĩnh sau khi gửi tháng đầu tiên là $1.000.000\left( 1+r \right)$
Tiếp tục cuối tháng anh Bình gửi 1 triệu đồng thì số tiền anh Bình được lĩnh sau khi gửi tháng thứ hai là
$\begin{array}{l} \left[ {1.000.000\left( {1 + r} \right) + 1.000.000} \right]\left( {1 + r} \right)\\ = 1.000.000{\left( {1 + r} \right)^2} + 1.000.000\left( {1 + r} \right)\\ = 1.000.000\left[ {{{\left( {1 + r} \right)}^2} + \left( {1 + r} \right)} \right] \end{array}$
Tiếp tục như vậy, sau $n$ tháng thì số tiền anh Bình có được là:
$\begin{array}{l} 1.000.000\left[ {{{\left( {1 + r} \right)}^n} + {{\left( {1 + r} \right)}^{n - 1}} + ... + \left( {1 + r} \right)} \right]\\ = 1.000.000\frac{{\left( {1 + r} \right)\left( {{{\left( {1 + r} \right)}^n} - 1} \right)}}{r} \end{array}$
Để có được 21 triệu đồng để mua được một chiếc xe máy thì cần tìm sao cho
$\begin{array}{l} 1.000.000\frac{{\left( {1 + r} \right)\left( {{{\left( {1 + r} \right)}^n} - 1} \right)}}{r} \ge 21.000.000\\ \Leftrightarrow \frac{{\left( {1 + r} \right)\left( {{{\left( {1 + r} \right)}^n} - 1} \right)}}{r} \ge 21 \end{array}$
Lãi suất $8%$/năm tương ứng với lãi suất $\frac{2}{3}%$/tháng.
Nên
$\begin{array}{l} \frac{{\left( {1 + \frac{2}{3}\% } \right)\left( {{{\left( {1 + \frac{2}{3}\% } \right)}^n} - 1} \right)}}{{\frac{2}{3}\% }} \ge 21\\ \Leftrightarrow n \ge {\log _{1 + \frac{2}{3}\% }}\left( {\frac{{21.\frac{2}{3}\% }}{{1 + \frac{2}{3}\% }} + 1} \right) \Leftrightarrow n \ge 19,59 \end{array}$
Nghía là anh Bình cần gửi tối thiểu 20 tháng thì sẽ đủ tiền để mua xe máy.
Đáp số: 5196
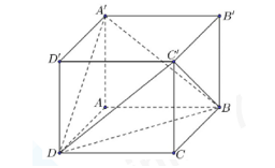
Giả sử $AB=a,\ A\text{D}=b,\ A{A}'=c$ thì thể tích khối hộp $ABCD.{A}'{B}'{C}'{D}'$ là $V=abc$.
Gọi khoảng cách từ đỉnh $A$ đến mặt phẳng $\left( {A}'BD \right)$ là $h$.
Xét hình chóp $A.A'BD$ có $A{A}',AB,AD$ đôi một vuông góc nên ta có $\frac{1}{{{h}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}+\frac{1}{{{c}^{2}}}$ $ \Rightarrow \frac{1}{{100}} = \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}$
Theo bất đẳng thức Cauchy ta có
$\begin{array}{l} \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}} \ge 3\sqrt[3]{{\frac{1}{{{a^2}{b^2}{c^2}}}}}\\ \Rightarrow \frac{1}{{100}} \ge 3\sqrt[3]{{\frac{1}{{{a^2}{b^2}{c^2}}}}}\\ \Rightarrow {a^2}{b^2}{c^2} \ge {27.100^3}\\ \Rightarrow {V^2} \ge {27.10^6} \Rightarrow V \ge 3000\sqrt 3 \end{array}$
Thể tích nhỏ nhất của khổi hộp $ABCD.{A}'{B}'{C}'{D}'$ là $5196$ (làm tròn kết quả đến hàng đơn vị), dấu bằng xảy ra khi $a=b=c=\sqrt{300}$.

Giả sử $AB=a,\ A\text{D}=b,\ A{A}'=c$ thì thể tích khối hộp $ABCD.{A}'{B}'{C}'{D}'$ là $V=abc$.
Gọi khoảng cách từ đỉnh $A$ đến mặt phẳng $\left( {A}'BD \right)$ là $h$.
Xét hình chóp $A.A'BD$ có $A{A}',AB,AD$ đôi một vuông góc nên ta có $\frac{1}{{{h}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}+\frac{1}{{{c}^{2}}}$ $ \Rightarrow \frac{1}{{100}} = \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}$
Theo bất đẳng thức Cauchy ta có
$\begin{array}{l} \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}} \ge 3\sqrt[3]{{\frac{1}{{{a^2}{b^2}{c^2}}}}}\\ \Rightarrow \frac{1}{{100}} \ge 3\sqrt[3]{{\frac{1}{{{a^2}{b^2}{c^2}}}}}\\ \Rightarrow {a^2}{b^2}{c^2} \ge {27.100^3}\\ \Rightarrow {V^2} \ge {27.10^6} \Rightarrow V \ge 3000\sqrt 3 \end{array}$
Thể tích nhỏ nhất của khổi hộp $ABCD.{A}'{B}'{C}'{D}'$ là $5196$ (làm tròn kết quả đến hàng đơn vị), dấu bằng xảy ra khi $a=b=c=\sqrt{300}$.
Đáp số: 3,74
Đổi $330\,\text{ml}=330\,\text{c}{{\text{m}}^{3}}$.
Gọi $r$ ($r>0$) là bán kính của hộp.

Thể tích của hộp $V=\pi {{r}^{2}}h=330\Rightarrow h=\frac{330}{\pi {{r}^{2}}}$.
Diện tích toàn phần của hộp
$\begin{align} & S=2\pi {{r}^{2}}+2\pi rh \\ & =2\pi {{r}^{2}}+2\pi r\cdot \frac{330}{\pi {{r}^{2}}} \\ & =2\pi {{r}^{2}}+2\cdot \frac{330}{r} \\ & =2\pi {{r}^{2}}+\frac{330}{r}+\frac{330}{r} \\ & \ge 3\sqrt[3]{2\pi {{r}^{2}}\cdot \frac{330}{r}\cdot \frac{330}{r}}=3\sqrt[3]{2\pi {{\left( 330 \right)}^{2}}}\approx 364,36\,(\text{c}{{\text{m}}^{2}}) \\ \end{align}$
Chi phí nhỏ nhất khi diện tích toàn phần của hộp là nhỏ nhất, điều này xảy ra khi $2\pi {{r}^{2}}=\frac{330}{r}\Leftrightarrow {{r}^{3}}=\frac{330}{2\pi }\Leftrightarrow r\approx 3,74$ (cm).
Đổi $330\,\text{ml}=330\,\text{c}{{\text{m}}^{3}}$.
Gọi $r$ ($r>0$) là bán kính của hộp.

Thể tích của hộp $V=\pi {{r}^{2}}h=330\Rightarrow h=\frac{330}{\pi {{r}^{2}}}$.
Diện tích toàn phần của hộp
$\begin{align} & S=2\pi {{r}^{2}}+2\pi rh \\ & =2\pi {{r}^{2}}+2\pi r\cdot \frac{330}{\pi {{r}^{2}}} \\ & =2\pi {{r}^{2}}+2\cdot \frac{330}{r} \\ & =2\pi {{r}^{2}}+\frac{330}{r}+\frac{330}{r} \\ & \ge 3\sqrt[3]{2\pi {{r}^{2}}\cdot \frac{330}{r}\cdot \frac{330}{r}}=3\sqrt[3]{2\pi {{\left( 330 \right)}^{2}}}\approx 364,36\,(\text{c}{{\text{m}}^{2}}) \\ \end{align}$
Chi phí nhỏ nhất khi diện tích toàn phần của hộp là nhỏ nhất, điều này xảy ra khi $2\pi {{r}^{2}}=\frac{330}{r}\Leftrightarrow {{r}^{3}}=\frac{330}{2\pi }\Leftrightarrow r\approx 3,74$ (cm).

Ước tính ở công đoạn tráng men, phần màu xanh có chi phí 50 nghìn đồng trên một mét vuông, còn phần màu trắng có chi phí 30 nghìn đồng trên một mét vuông. Tính chi phí (đơn vị: tỉ đồng) của công đoạn tráng men này, khi cơ sở dự định sản xuất $100\,000$ viên gạch như thế (làm tròn kết quả đến hàng phần trăm).
Đáp số: 2,65

Xét $\frac{1}{16}$ viên gạch men (vùng hình vuông chứa một cánh hoa).
Vì phần cánh hoa (màu xanh) là phần giao nhau của các đường tròn có khoảng cách giữa các tâm là $20\sqrt{2}$ nên một cánh hoa là phần giao của hai phần tư hình tròn tâm $A,B$ (hình vẽ), có bán kính $r=20$.
Mỗi phần tư hình tròn tâm $A$, $B$ có diện tích $S=\frac{1}{4}\pi \cdot {{20}^{2}}$.
Diện tích hình vuông có $AB$ là đường chéo: ${{S}_{v}}={{20}^{2}}$.
Suy ra diện tích của một cánh hoa là $2S-{{S}_{v}}=\frac{1}{2}\pi \cdot {{20}^{2}}-{{20}^{2}}=\left( \frac{\pi }{2}-1 \right)\cdot {{20}^{2}}$.
Do đó
Diện tích phần màu xanh là ${{S}_{1}}=16\left( \frac{\pi }{2}-1 \right)\cdot {{20}^{2}}$ ($\text{c}{{\text{m}}^{2}}$).
Diện tích phần màu trắng ${{S}_{2}}={{80}^{2}}-{{S}_{1}}$ ($\text{c}{{\text{m}}^{2}}$).
Số tiền tráng men một viên gạch là $T=5{{S}_{1}}+3{{S}_{2}}=26\,506,192\,98$ đồng.
Để sản xuất $100\,000$ viên gạch thì số tiền tráng men là x $100\,000T=2\,650\,619\,298\,\left( vnd \right)\approx 2,65\,(ti\,dong)$..

Xét $\frac{1}{16}$ viên gạch men (vùng hình vuông chứa một cánh hoa).
Vì phần cánh hoa (màu xanh) là phần giao nhau của các đường tròn có khoảng cách giữa các tâm là $20\sqrt{2}$ nên một cánh hoa là phần giao của hai phần tư hình tròn tâm $A,B$ (hình vẽ), có bán kính $r=20$.
Mỗi phần tư hình tròn tâm $A$, $B$ có diện tích $S=\frac{1}{4}\pi \cdot {{20}^{2}}$.
Diện tích hình vuông có $AB$ là đường chéo: ${{S}_{v}}={{20}^{2}}$.
Suy ra diện tích của một cánh hoa là $2S-{{S}_{v}}=\frac{1}{2}\pi \cdot {{20}^{2}}-{{20}^{2}}=\left( \frac{\pi }{2}-1 \right)\cdot {{20}^{2}}$.
Do đó
Diện tích phần màu xanh là ${{S}_{1}}=16\left( \frac{\pi }{2}-1 \right)\cdot {{20}^{2}}$ ($\text{c}{{\text{m}}^{2}}$).
Diện tích phần màu trắng ${{S}_{2}}={{80}^{2}}-{{S}_{1}}$ ($\text{c}{{\text{m}}^{2}}$).
Số tiền tráng men một viên gạch là $T=5{{S}_{1}}+3{{S}_{2}}=26\,506,192\,98$ đồng.
Để sản xuất $100\,000$ viên gạch thì số tiền tráng men là x $100\,000T=2\,650\,619\,298\,\left( vnd \right)\approx 2,65\,(ti\,dong)$..
