Thí sinh trả lời từ câu 1 đến câu 18. Mỗi câu hỏi thí sinh chỉ chọn một phương án.PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
Câu 1: Động năng tịnh tiến trung bình của phân tử khí phụ thuộc
A. vào bản chất chất khí.
B. nhiệt độ của khối khí.
C. áp suất chất khí.
D. mật độ phân tử khí.
$W_d=\frac{3}{2} k T$. Chọn B
A. $1 \mathrm{~m}^3$ chất đó tăng thêm 1 K (hoặc $1^{\circ} \mathrm{C}$ ).
B. 1 mol chất đó tăng thêm 1 K (hoặc $1^{\circ} \mathrm{C}$ ).
C. 1 kg chất đó tăng thêm 1 K (hoặc $1^{\circ} \mathrm{C}$ ).
D. 1 phân tử chất đó tăng thêm 1 K (hoặc $1^{\circ} \mathrm{C}$ ).
Chọn C
A. Các tia $\alpha, \beta, \gamma$ đều có chung bản chất là sóng điện từ nhưng có bước sóng khác nhau.
B. Tia $\beta^{+}$là dòng các hạt positron.
C. Tia $\beta^{-}$là dòng các hat electron.
D. Tia $\alpha$ là dòng các hạt nhân nguyên tử ${ }_2^4 \mathrm{He}$.
Tia $\alpha, \beta$ không phải là sóng điện từ. Chọn A
A. $\mathrm{m}_\alpha<2 \mathrm{~m}_{\mathrm{p}}+2 \mathrm{~m}_{\mathrm{n}}$.
B. $\mathrm{m}_\alpha>2 \mathrm{~m}_{\mathrm{p}}+2 \mathrm{~m}_{\mathrm{n}}$.
C. $\mathrm{m}_\alpha=2 \mathrm{~m}_{\mathrm{p}}+2 \mathrm{~m}_{\mathrm{n}}$.
D. $\mathrm{m}_\alpha=\mathrm{m}_{\mathrm{p}}+\mathrm{m}_{\mathrm{n}}$.
Do có độ hụt khối. Chọn A
A. tỉ lệ thuận với nhiệt độ tuyệt đối.
B. luôn tăng khi thay đổi nhiệt độ.
C. luôn giảm khi thay đổi nhiệt độ.
D. luôn giữ không đổi.
Đẳng tích $\frac{p}{T}=$ const . Chọn A
A. 283 V .
B. 141 V .
C. 200 V .
D. 100 V .
$U=\frac{U_0}{\sqrt{2}}=\frac{200}{\sqrt{2}}=100 \sqrt{2} V$. Chọn B
A. +1 e.
B. 0 .
C. +2 e .
D. +3 e .
$1+Z=2+0 \Rightarrow Z=1$. Chọn A
A. $8,579 \mathrm{MeV} /$ nucleon .
B. $7,148 \mathrm{MeV} /$ nucleon .
C. $17,16 \mathrm{MeV} /$ nucleon .
D. $343,2 \mathrm{MeV} /$ nucleon .
${{W}_{lk}}=\Delta m{{c}^{2}}=0,3684.931,5=343,1646\text{MeV}$
${{W}_{lkr}}=\frac{{{W}_{lk}}}{A}=\frac{343,1646}{40}\approx 8,579\text{MeV}/\text{ nucleon}$
Chọn A
${{W}_{lkr}}=\frac{{{W}_{lk}}}{A}=\frac{343,1646}{40}\approx 8,579\text{MeV}/\text{ nucleon}$
Chọn A
A. 252 lít.
B. 18 lít.
C. 50 lít.
D. 200 lít.
$\begin{array}{l} \frac{V}{T} = {\rm{ const }}\\ \Rightarrow \frac{{30}}{{27 + 273}} = \frac{V}{{227 + 273}}\\ \Rightarrow V = 50l{\rm{. }} \end{array}$
Chọn C
Chọn C
A. $6,7 \cdot 10^{-3} \mathrm{~T}$.
B. $1,8 \cdot 10^{-3} \mathrm{~T}$.
C. $1,5 \mathrm{~T}$.
D. $0,60 \mathrm{~T}$.
$F=\Pi B \Rightarrow 3=10.0,5 . B \Rightarrow B=0,6 T$. Chọn D
A. $4,54 \mathrm{~kg}$.
B. $0,562 \mathrm{~kg}$.
C. $0,456 \mathrm{~kg}$.
D. $5,62 \mathrm{~kg}$.
$\begin{array}{l} {m_c}{c_c}\left( {{t_c} - t} \right) = {m_n}{c_n}\left( {t - {t_n}} \right)\\ \Rightarrow 0,5.880.(100 - 35) = {m_n}.4180.(35 - 20)\\ \Rightarrow {m_n} \approx 0,456\;{\rm{kg}} \end{array}$
. Chọn C
. Chọn C
A. $671^{\circ} \mathrm{C}$
B. $86^{\circ} \mathrm{C}$
C. $857^{\circ} \mathrm{C}$
D. $398^{\circ} \mathrm{C}$
$\begin{array}{l} \frac{{pV}}{T} = {\rm{const}}\\ \Rightarrow \frac{{1.2,8}}{{40 + 273}} = \frac{{20.0,3}}{T}\\ \Rightarrow T \approx 671K = {398^0}{\rm{C}}. \end{array}$
Chọn D
Chọn D
A. $9,42 \mathrm{mV}$.
B. $2,5 \mathrm{~V}$.
C. $9,42 \cdot 10^{-5} \mathrm{~V}$.
D. $2,5 \cdot 10^{-5} \mathrm{~V}$.
$T=\frac{1}{f}=\frac{1}{2}=0,5s(\text{rad}/\text{s})$
$\begin{array}{l} e = \left| {\frac{{\Delta \phi }}{{\Delta t}}} \right| = \left| {\frac{{BS}}{T}} \right|\\ = \left| {\frac{{B\pi {R^2}}}{T}} \right|\\ = \left| {\frac{{{{6.10}^{ - 5}} \cdot \pi {{.0,5}^2}}}{{0,5}}} \right|\\ \approx {9,42.10^{ - 5}}V. \end{array}$
Chọn C
$\begin{array}{l} e = \left| {\frac{{\Delta \phi }}{{\Delta t}}} \right| = \left| {\frac{{BS}}{T}} \right|\\ = \left| {\frac{{B\pi {R^2}}}{T}} \right|\\ = \left| {\frac{{{{6.10}^{ - 5}} \cdot \pi {{.0,5}^2}}}{{0,5}}} \right|\\ \approx {9,42.10^{ - 5}}V. \end{array}$
Chọn C
A. nhận công là 20 J .
B. nhận công là 40 J .
C. sinh công là 40 J .
D. thực hiện công là 20 J .
$\begin{align} & \Delta U=Q+A \\ & \Rightarrow 10=30+A \\ & \Rightarrow A=-20J\text{. } \\ \end{align}$
Chọn D
Chọn D
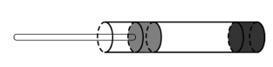
Giấy được làm ẩm, vò lại và nhét chặt vào một đầu của ống tre (trúc) hình trụ rỗng. Nút cao su được đẩy từ đầu bên kia của ống, nén không khí trong ống lại cho đến khi giấy được bắn đi (hình vẽ minh họa). Ta coi như dùng mô hình khí lí tưởng cho khối khí bên trong ống. Ban đầu, thể tích khí giới hạn trong ống là V, áp suất là $\mathrm{p}=10^5 \mathrm{~Pa}$. Khi thể tích khí trong ống bằng $20 \%$ thể tích ban đầu thì áp suất khí có giá trị là p'. Lúc này, lực nén lên giấy làm nó được bắn đi. Xem như nhiệt độ khí không đổi và lượng khí xì ra khỏi ống không đáng kể.
Câu 15: Giá trị của p' bằng
A. $10^6 \mathrm{~Pa}$.
B. $1,25 \cdot 10^5 \mathrm{~Pa}$.
C. $2.10^4 \mathrm{~Pa}$.
D. $5.10^5 \mathrm{~Pa}$.
Đẳng nhiệt
$\begin{array}{l} \Rightarrow pV = p'V'\\ \Rightarrow {10^5} = p'.0,2\\ \Rightarrow p' = {5.10^5}\;{\rm{Pa}} \end{array}$
Chọn D
$\begin{array}{l} \Rightarrow pV = p'V'\\ \Rightarrow {10^5} = p'.0,2\\ \Rightarrow p' = {5.10^5}\;{\rm{Pa}} \end{array}$
Chọn D
A. $3,2 \mathrm{~m} / \mathrm{s}$.
B. $4 \mathrm{~m} / \mathrm{s}$.
C. $5 \mathrm{~m} / \mathrm{s}$.
D. $40 \mathrm{~m} / \mathrm{s}$.
$F=\left( {{p}^{\prime }}-{{p}_{0}} \right)S=\left( {{5.10}^{5}}-{{10}^{5}} \right)\cdot 8\cdot {{10}^{-5}}=32N$
Biến thiên động lượng = xung lượng của lực
$\Rightarrow m v=F \Delta t \Rightarrow 0,1 . v=32.0,01 \Rightarrow v=3,2 \mathrm{~m} / \mathrm{s}$. Chọn A
Biến thiên động lượng = xung lượng của lực
$\Rightarrow m v=F \Delta t \Rightarrow 0,1 . v=32.0,01 \Rightarrow v=3,2 \mathrm{~m} / \mathrm{s}$. Chọn A
A. $1,61 \cdot 10^{19} \mathrm{~Bq}$.
B. $3,87.10^{13} \mathrm{~Bq}$.
C. $3,87.10^{19} \mathrm{~Bq}$.
D. $1,61.10^{12} \mathrm{~Bq}$.
$n=CV=1,002\cdot {{10}^{-3}}\cdot 5\cdot {{10}^{-3}}=5,01\cdot {{10}^{-6}}~\text{mol}$
$N=n{{N}_{A}}=5,01\cdot {{10}^{-6}}\cdot 6,02\cdot {{10}^{23}}=3,01602\cdot {{10}^{18}}$
$\begin{array}{l} H = \lambda N = \frac{{\ln 2}}{T} \cdot N\\ = \frac{{\ln 2}}{{15 \cdot 60 \cdot 60}} \cdot 3,01602 \cdot {10^{18}}\\ \approx 3,87 \cdot {10^{13}}\;{\rm{Bq}}.{\rm{ }} \end{array}$
Chọn B
$N=n{{N}_{A}}=5,01\cdot {{10}^{-6}}\cdot 6,02\cdot {{10}^{23}}=3,01602\cdot {{10}^{18}}$
$\begin{array}{l} H = \lambda N = \frac{{\ln 2}}{T} \cdot N\\ = \frac{{\ln 2}}{{15 \cdot 60 \cdot 60}} \cdot 3,01602 \cdot {10^{18}}\\ \approx 3,87 \cdot {10^{13}}\;{\rm{Bq}}.{\rm{ }} \end{array}$
Chọn B
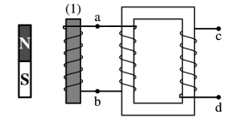
A. $\mathrm{V}_{\mathrm{a}}<\mathrm{V}_{\mathrm{b}}, \mathrm{V}_{\mathrm{c}}<\mathrm{V}_{\mathrm{d}}$.
B. $V_a>V_b, V_c>V_d$.
C. $V_a>V_b, V_c<V_d$.
D. $V_a<V_b, V_c>V_d$.
Theo quy tắc vào nam ra bắc (vào S ra N ) thì đường sức từ đi qua ống dây từ trên xuống
Nam châm lại gần $\Rightarrow$ từ thông tăng $\Rightarrow \overrightarrow{B_{c u}} \uparrow \downarrow \vec{B} \Rightarrow \overrightarrow{B_{c u}}$ trong ống dây hướng lên
Áp dụng quy tắc nắm tay phải $\Rightarrow$ dòng điện đi từ a qua cuộn sơ cấp đến $\mathrm{b} \Rightarrow V_a>V_b$
Áp dụng quy tắc nắm tay phải $\Rightarrow$ đường sức từ trong lòng cuộn sơ cấp hướng lên $\Rightarrow$ đường sức từ trong lòng cuộn thứ cấp hướng xuống $\Rightarrow \overrightarrow{B_{c u}}$ trong lòng cuộn thứ cấp hướng lên $\Rightarrow V_d>V_c$.
Chọn C
Nam châm lại gần $\Rightarrow$ từ thông tăng $\Rightarrow \overrightarrow{B_{c u}} \uparrow \downarrow \vec{B} \Rightarrow \overrightarrow{B_{c u}}$ trong ống dây hướng lên
Áp dụng quy tắc nắm tay phải $\Rightarrow$ dòng điện đi từ a qua cuộn sơ cấp đến $\mathrm{b} \Rightarrow V_a>V_b$
Áp dụng quy tắc nắm tay phải $\Rightarrow$ đường sức từ trong lòng cuộn sơ cấp hướng lên $\Rightarrow$ đường sức từ trong lòng cuộn thứ cấp hướng xuống $\Rightarrow \overrightarrow{B_{c u}}$ trong lòng cuộn thứ cấp hướng lên $\Rightarrow V_d>V_c$.
Chọn C
Thí sinh trả lòi từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.PHẦN II. Câu trắc nghiệm đúng sai.
Câu 1: Các đồ thị sau đây mô tả sự biến đổi trạng thái của một lượng khí xác định theo các quá trình khác nhau.
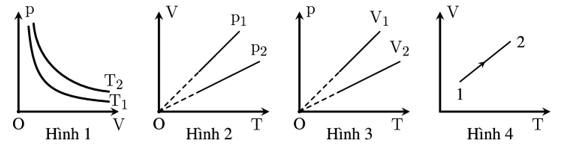
a) Ở đồ thị hình 1: Quá trình biến đổi có $\mathrm{T}_2<\mathrm{T}_1$.
b) Ở đồ thị hình 2: Quá trình biến đổi có $\mathrm{p}_2>\mathrm{p}_1$.
c) Ở đồ thị hình 3: Quá trình biến đổi có $V_2>V_1$.
d) Ở đồ thị hình 4: Quá trình biến đổi từ 1 đến 2 có áp suất, thể tích và nhiệt độ đều tăng.
a) Sai. Xét cùng V thì $\mathrm{p}_2>\mathrm{p}_1 \Rightarrow \mathrm{~T}_2>\mathrm{T}_1$
b) Đúng. $\frac{p V}{T}=C \Rightarrow V=\frac{C}{p} \cdot T \Rightarrow$ hệ số góc $\frac{C}{p_1}>\frac{C}{p_2} \Rightarrow p_1<p_2$
c) Đúng. $\frac{p V}{T}=C \Rightarrow p=\frac{C}{V} \cdot T \Rightarrow$ hệ số góc $\frac{C}{V_1}>\frac{C}{V_2} \Rightarrow V_1<V_2$
d) Đúng. $\frac{p V}{T}=C \Rightarrow V=\frac{C}{p} \cdot T \Rightarrow$ hệ số góc $\frac{C}{p_1}>\frac{C}{p_2} \Rightarrow p_1<p_2$
b) Đúng. $\frac{p V}{T}=C \Rightarrow V=\frac{C}{p} \cdot T \Rightarrow$ hệ số góc $\frac{C}{p_1}>\frac{C}{p_2} \Rightarrow p_1<p_2$
c) Đúng. $\frac{p V}{T}=C \Rightarrow p=\frac{C}{V} \cdot T \Rightarrow$ hệ số góc $\frac{C}{V_1}>\frac{C}{V_2} \Rightarrow V_1<V_2$
d) Đúng. $\frac{p V}{T}=C \Rightarrow V=\frac{C}{p} \cdot T \Rightarrow$ hệ số góc $\frac{C}{p_1}>\frac{C}{p_2} \Rightarrow p_1<p_2$
a) Sản phẩm của sự phóng xạ ${ }^{238} \mathrm{Pu}$ là hạt nhân có số nucleon bằng 236.
b) Độ phóng xạ ban đầu của khối chất ${ }^{238} \mathrm{Pu}$ là $7.10^{15} \mathrm{~Bq}$.
c) Mỗi phản ứng phóng xạ của ${ }^{238} \mathrm{Pu}$ tỏa năng lượng là $5,6 \mathrm{MeV}$ (làm tròn đến chữ số phần mười).
d) Công suất điện phát ra ban đầu là $4,99 \mathrm{~kW}$.
${ }^{238} \mathrm{Pu} \rightarrow{ }_2^4 \alpha+{ }^{234} \mathrm{X} \Rightarrow \mathrm{X}$ có 234 nucleon $\Rightarrow$ a) Sai
$n=\frac{m}{M}=\frac{11.10^3}{238}=\frac{5500}{119} \mathrm{~mol}$
$N_0=n N_A=\frac{5500}{119} \cdot 6,02 \cdot 10^{23} \approx 2,7824 \cdot 10^{25}$
$\begin{array}{l} {H_0} = \lambda {N_0} = \frac{{\ln 2}}{T} \cdot {N_0}\\ = \frac{{\ln 2}}{{87,7.365 \cdot 24.60.60}} \cdot 2,7824 \cdot {10^{25}}\\ \approx {6,97.10^{15}}\;{\rm{Bq}} \end{array}$
b) Đúng
Bảo toàn động lượng
$\begin{array}{l} p_\alpha ^2 = p_X^2\\ \Rightarrow 2{m_\alpha }{K_\alpha } = 2{m_X}{K_X}\\ \Rightarrow {K_X} = \frac{{{m_\alpha }{K_\alpha }}}{{{m_X}}}\\ = \frac{{4.5,49}}{{234}} = \frac{{61}}{{650}}{\rm{MeV}} \end{array}$
$\begin{array}{l} \Delta E = {K_\alpha } + {K_X}\\ = 5,49 + \frac{{61}}{{650}} \approx 5,6{\rm{MeV}} \end{array}$
c) Đúng
$\begin{array}{l} {P_0} = {H_0}{K_\alpha }\\ = 6,97 \cdot {10^{15}} \cdot 5,59 \cdot 1,6 \cdot {10^{ - 13}}\\ \approx 6,2 \cdot {10^3}W = 6,2\;{\rm{kW}} \end{array}$
d) Sai
$n=\frac{m}{M}=\frac{11.10^3}{238}=\frac{5500}{119} \mathrm{~mol}$
$N_0=n N_A=\frac{5500}{119} \cdot 6,02 \cdot 10^{23} \approx 2,7824 \cdot 10^{25}$
$\begin{array}{l} {H_0} = \lambda {N_0} = \frac{{\ln 2}}{T} \cdot {N_0}\\ = \frac{{\ln 2}}{{87,7.365 \cdot 24.60.60}} \cdot 2,7824 \cdot {10^{25}}\\ \approx {6,97.10^{15}}\;{\rm{Bq}} \end{array}$
b) Đúng
Bảo toàn động lượng
$\begin{array}{l} p_\alpha ^2 = p_X^2\\ \Rightarrow 2{m_\alpha }{K_\alpha } = 2{m_X}{K_X}\\ \Rightarrow {K_X} = \frac{{{m_\alpha }{K_\alpha }}}{{{m_X}}}\\ = \frac{{4.5,49}}{{234}} = \frac{{61}}{{650}}{\rm{MeV}} \end{array}$
$\begin{array}{l} \Delta E = {K_\alpha } + {K_X}\\ = 5,49 + \frac{{61}}{{650}} \approx 5,6{\rm{MeV}} \end{array}$
c) Đúng
$\begin{array}{l} {P_0} = {H_0}{K_\alpha }\\ = 6,97 \cdot {10^{15}} \cdot 5,59 \cdot 1,6 \cdot {10^{ - 13}}\\ \approx 6,2 \cdot {10^3}W = 6,2\;{\rm{kW}} \end{array}$
d) Sai
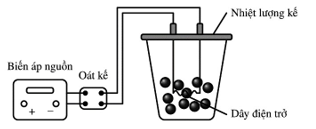
a) Ở áp suất tiêu chuẩn, nưởc đá tinh khiết nóng chảy ở nhiệt độ $100^{\circ} \mathrm{C}$.
b) Khi nóng chảy hoàn toàn, thể tích nước tạo thành lớn hơn tổng thể tích nước đá ban đầu.
c) Nhiệt lượng nước đá nhận được từ dây điện trở trong thời gian đun là 4320 J .
d) Nhiệt nóng chảy riêng $\lambda$ của nước đá đo được là $3,3.10^5 \mathrm{~J} / \mathrm{kg}$.
a) Sai. Ở áp suất tiêu chuẩn, nước đá tinh khiết nóng chảy ở nhiệt độ $0^{\circ} \mathrm{C}$.
b) Sai. Thể tích nước nhỏ hơn thể tích nước đá
c) Đúng. $Q=P t=24.180=4320 \mathrm{~J}$
d) Sai. $\lambda=\frac{Q}{m}=\frac{4320}{0,015}=2,88 \cdot 10^5 \mathrm{~J} / \mathrm{kg}$
b) Sai. Thể tích nước nhỏ hơn thể tích nước đá
c) Đúng. $Q=P t=24.180=4320 \mathrm{~J}$
d) Sai. $\lambda=\frac{Q}{m}=\frac{4320}{0,015}=2,88 \cdot 10^5 \mathrm{~J} / \mathrm{kg}$
a) Công suất tỏa nhiệt của các cuộn dây của động cơ bằng 6 W .
b) Công suất của nguồn điện bằng 46 W .
c) Hiệu suất của động cơ (tỉ số giữa công suất có ích và công suất toàn phần của động cơ) khoảng $87 \%$.
d) Nếu động cơ bị kẹt (không quay) thì cường độ dòng điện qua động cơ bằng 10 A
${{P}_{R}}={{I}^{2}}R={{2}^{2}}\cdot 1,5=6~\text{W}\Rightarrow $a) Đúng
${{P}_{ng}}=EI=25\cdot 2=50~\text{W}\Rightarrow $b) Sai
${{P}_{r}}={{I}^{2}}r={{2}^{2}}\cdot 1=4~\text{W}$
${{P}_{tp}}={{P}_{ng}}-{{R}_{r}}=50-4=46~\text{W}$
${{P}_{ci}}={{P}_{tp}}-{{P}_{R}}=46-6=40~\text{W}$
$H=\frac{{{P}_{ci}}}{{{P}_{tp}}}=\frac{40}{46}\approx 0,87=87%\Rightarrow $c) Đúng
${{I}_{\text{ket }}}=\frac{E}{R+r}=\frac{25}{1,5+1}=10~\text{A}\Rightarrow $d) Đúng
${{P}_{ng}}=EI=25\cdot 2=50~\text{W}\Rightarrow $b) Sai
${{P}_{r}}={{I}^{2}}r={{2}^{2}}\cdot 1=4~\text{W}$
${{P}_{tp}}={{P}_{ng}}-{{R}_{r}}=50-4=46~\text{W}$
${{P}_{ci}}={{P}_{tp}}-{{P}_{R}}=46-6=40~\text{W}$
$H=\frac{{{P}_{ci}}}{{{P}_{tp}}}=\frac{40}{46}\approx 0,87=87%\Rightarrow $c) Đúng
${{I}_{\text{ket }}}=\frac{E}{R+r}=\frac{25}{1,5+1}=10~\text{A}\Rightarrow $d) Đúng
Thí sinh trả lòi từ câu 1 đến câu 6 .PHẨN III. Câu trắc nghiệm trả lời ngắn.
Sử dụng thông tin sau cho câu 1 và câu 2 : Để xác định nhiệt dung riêng của một chất lỏng, người ta đổ chất lỏng đó vào 20 g nước ở $100^{\circ} \mathrm{C}$. Khi có sự cân bằng nhiệt, nhiệt độ của hỗn hợp là $37,5^{\circ} \mathrm{C}$ và khối lượng hỗn hợp là $\mathrm{m}=140 \mathrm{~g}$. Biết nhiệt độ ban đầu của chất lỏng là $20^{\circ} \mathrm{C}$, nhiệt dung riêng của nước là $\mathrm{c}=$ $4200 \mathrm{~J} / \mathrm{kg}$. K.
Câu 1: Nhiệt lượng nước tỏa ra cho đến khi có sự cân bằng nhiệt là bao nhiêu J?
$\begin{array}{l} Q = {m_n}{c_n}\left( {{t_n} - t} \right)\\ = 0,02.4200.(100 - 37,5) = 5250\;{\rm{J}} \end{array}$
Trả lời ngắn: 5250
Trả lời ngắn: 5250
$\begin{array}{l} Q = {m_l}{c_l}\left( {t - {t_l}} \right)\\ \Rightarrow 5250 = (0,14 - 0,02) \cdot {c_l} \cdot (37,5 - 20)\\ \Rightarrow {c_l} = 2500\;{\rm{J}}/{\rm{kgK}} \end{array}$
Trả lời ngắn: 2500
Trả lời ngắn: 2500
Câu 3: Tần số của dòng điện do máy phát ra là bao nhiêu Hz ?
$f=40~\text{Hz}$
Trả lời ngắn: 40
Trả lời ngắn: 40
$\omega =2\pi f=2\pi .40=80\pi (\text{rad}/\text{s})$
$\begin{array}{l} {E_0} = NBS\omega \\ \Rightarrow 40 = 500.B{.0,25^2}.80\pi \\ \Rightarrow B \approx {5,1.10^{ - 3}}T = 5,1{\rm{mT}} \end{array}$
Trả lời ngắn: 5,1
Sử dụng thông tin sau cho câu 5 và 6: Sơn tĩnh điện là một ứng dụng của lực tương tác tĩnh điện giữa hai điện tích. Các hạt bột sơn sẽ được nhiễm điện và phun vào bề mặt vật liệu sơn. Nhờ lực hút tĩnh điện, các hạt sơn này bám rất chặt trên bề mặt vật liệu. Bài toán sau đây minh họa cho tương tác tĩnh điện giữa hai điện tích trái dấu: Một vật A có điện tích $\mathrm{Q}=-8 \cdot 10^{-6} \mathrm{C}$ được cố định tại một điểm trong chân không. Một vật B có khối lượng $\mathrm{m}=10 \mathrm{~g}$, mang điện tích $\mathrm{q}=8.10^{-6} \mathrm{C}$ được bắn trực diện vào vật A từ vị trí M cách A một đoạn 20 cm . Xem các vật như điện tích điểm; lấy $\mathrm{k}=9.10^9 \mathrm{Nm}^2 . \mathrm{C}^{-2}$.
$\begin{array}{l} {E_0} = NBS\omega \\ \Rightarrow 40 = 500.B{.0,25^2}.80\pi \\ \Rightarrow B \approx {5,1.10^{ - 3}}T = 5,1{\rm{mT}} \end{array}$
Trả lời ngắn: 5,1
Sử dụng thông tin sau cho câu 5 và 6: Sơn tĩnh điện là một ứng dụng của lực tương tác tĩnh điện giữa hai điện tích. Các hạt bột sơn sẽ được nhiễm điện và phun vào bề mặt vật liệu sơn. Nhờ lực hút tĩnh điện, các hạt sơn này bám rất chặt trên bề mặt vật liệu. Bài toán sau đây minh họa cho tương tác tĩnh điện giữa hai điện tích trái dấu: Một vật A có điện tích $\mathrm{Q}=-8 \cdot 10^{-6} \mathrm{C}$ được cố định tại một điểm trong chân không. Một vật B có khối lượng $\mathrm{m}=10 \mathrm{~g}$, mang điện tích $\mathrm{q}=8.10^{-6} \mathrm{C}$ được bắn trực diện vào vật A từ vị trí M cách A một đoạn 20 cm . Xem các vật như điện tích điểm; lấy $\mathrm{k}=9.10^9 \mathrm{Nm}^2 . \mathrm{C}^{-2}$.

$F=k\cdot \frac{|Qq|}{{{r}^{2}}}={{9.10}^{9}}\cdot \frac{\left| 8\cdot {{10}^{-6}}\cdot 8\cdot {{10}^{-6}} \right|}{{{0,2}^{2}}}=14,4N$
Trả lời ngắn: 14,4
Trả lời ngắn: 14,4
Cách 1:
$\begin{array}{l} F = ma\\ \Rightarrow k \cdot \frac{{Qq}}{{{r^2}}} = m\frac{{dv}}{{dt}}\\ \Rightarrow k \cdot \frac{{Qq}}{{{r^2}}}dr = m\frac{{dv}}{{dt}} \cdot dr\\ \Rightarrow k \cdot \frac{{Qq}}{{{r^2}}}dr = mvdv\\ \Rightarrow \int_{0,2}^{0,1} k \cdot \frac{{Qq}}{{{r^2}}}dr = \int_{10}^v m vdv \end{array}$
$ \Rightarrow \int_{0,2}^{0,1} 9 {.10^9} \cdot \frac{{ - {{\left( {{{8.10}^{ - 6}}} \right)}^2}}}{{{r^2}}}dr$ $ = \int_{10}^v 1 {0.10^{ - 3}}vdv$ $ \Rightarrow 2,88 = \int_{10}^v 1 {0.10^{ - 3}}vdv$ $\xrightarrow{\text{ shifsolve }}v=26~\text{m}/\text{s}$
Cách 2: Bảo toàn cơ năng được
$\begin{array}{l} {W_{d1}} + {W_{t1}} = {W_{d2}} + {W_{t2}}\\ \Rightarrow \frac{1}{2}mv_1^2 + k \cdot \frac{{Qq}}{{{r_1}}}\\ = \frac{1}{2}mv_2^2 + k \cdot \frac{{Qq}}{{{r_2}}} \end{array}$
$\begin{array}{l} \Rightarrow \frac{1}{2} \cdot 10 \cdot {10^{ - 3}} \cdot {10^2} + 9 \cdot {10^9} \cdot \frac{{ - 8 \cdot {{10}^{ - 6}} \cdot 8 \cdot {{10}^{ - 6}}}}{{0,2}}\\ = \frac{1}{2} \cdot 10 \cdot {10^{ - 3}} \cdot v_2^2 + 9 \cdot {10^9} \cdot \frac{{ - 8 \cdot {{10}^{ - 6}} \cdot 8 \cdot {{10}^{ - 6}}}}{{0,1}}\\ \Rightarrow {v_2} = 26\;{\rm{m}}/{\rm{s}} \end{array}$
Trả lời ngắn: 26
$\begin{array}{l} F = ma\\ \Rightarrow k \cdot \frac{{Qq}}{{{r^2}}} = m\frac{{dv}}{{dt}}\\ \Rightarrow k \cdot \frac{{Qq}}{{{r^2}}}dr = m\frac{{dv}}{{dt}} \cdot dr\\ \Rightarrow k \cdot \frac{{Qq}}{{{r^2}}}dr = mvdv\\ \Rightarrow \int_{0,2}^{0,1} k \cdot \frac{{Qq}}{{{r^2}}}dr = \int_{10}^v m vdv \end{array}$
$ \Rightarrow \int_{0,2}^{0,1} 9 {.10^9} \cdot \frac{{ - {{\left( {{{8.10}^{ - 6}}} \right)}^2}}}{{{r^2}}}dr$ $ = \int_{10}^v 1 {0.10^{ - 3}}vdv$ $ \Rightarrow 2,88 = \int_{10}^v 1 {0.10^{ - 3}}vdv$ $\xrightarrow{\text{ shifsolve }}v=26~\text{m}/\text{s}$
Cách 2: Bảo toàn cơ năng được
$\begin{array}{l} {W_{d1}} + {W_{t1}} = {W_{d2}} + {W_{t2}}\\ \Rightarrow \frac{1}{2}mv_1^2 + k \cdot \frac{{Qq}}{{{r_1}}}\\ = \frac{1}{2}mv_2^2 + k \cdot \frac{{Qq}}{{{r_2}}} \end{array}$
$\begin{array}{l} \Rightarrow \frac{1}{2} \cdot 10 \cdot {10^{ - 3}} \cdot {10^2} + 9 \cdot {10^9} \cdot \frac{{ - 8 \cdot {{10}^{ - 6}} \cdot 8 \cdot {{10}^{ - 6}}}}{{0,2}}\\ = \frac{1}{2} \cdot 10 \cdot {10^{ - 3}} \cdot v_2^2 + 9 \cdot {10^9} \cdot \frac{{ - 8 \cdot {{10}^{ - 6}} \cdot 8 \cdot {{10}^{ - 6}}}}{{0,1}}\\ \Rightarrow {v_2} = 26\;{\rm{m}}/{\rm{s}} \end{array}$
Trả lời ngắn: 26
