TangGiap giới thiệu đề thi thử THPT Quốc gia 2025 môn Vật Lí do Trường THPT Hoàng Văn Thụ (Nam Định) biên soạn. Đề thi được xây dựng bám sát cấu trúc của Bộ Giáo dục và Đào tạo, phù hợp với xu hướng ra đề mới nhất. Đây là tài liệu luyện thi hữu ích, giúp học sinh lớp 12 rèn luyện kỹ năng giải đề, nâng cao tư duy và chuẩn bị tốt cho kỳ thi chính thức. Đề thi có thể kèm theo đáp án và lời giải chi tiết, hỗ trợ học sinh tự học hiệu quả tại nhà.
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 18. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 Câu nào sau đây nói về truyền nhiệt và thực hiện công là không đúng?
A. Thực hiện công là quá trình có thể làm thay đổi nội năng của vật.
B. Truyền nhiệt là quá trình có thể làm thay đổi nội năng của vật.
C. Trong thực hiện công có sự chuyển hoá năng lượng.
D. Trong truyền nhiệt có sự chuyển hoá năng lượng.
Câu 2 Một khối nước đá ở $0^{\circ} \mathrm{C}$ có khối lượng mo nhận nhiệt lượng 396 kJ thì thấy $20 \%$ khối lượng nước đá đã bị nóng chảy. Biết nhiệt nóng chảy riêng của nước đá là $3,3 \cdot 10^5 \mathrm{~J} / \mathrm{kg}$. Giá trị của $\mathrm{m}_0$ bằng
A. 6 g .
B. $1,2 \mathrm{~g}$.
C. 6 kg .
D. $1,2 \mathrm{~kg}$.
Sử dụng các thông tin sau cho Câu 3 và Câu 4: Máy nước nóng trực tiếp OTTOWA là dòng máy làm nóng nước tức thời. Nước lạnh chảy vào bình được thanh đốt trong ống làm nóng chỉ trong vài giây. Thanh điện trở trong máy nước nóng trực tiếp hoạt động dựa trên nguyên lý mở khi có nước chảy và tự động ngắt khi không có nước chảy nhờ một công tắc đóng bên trong. Ngoài ra, trong bộ mạch điện máy nước nóng trực tiếp của OTTOWA còn có thêm bộ phận ELCB chống giật, đảm bảo an toàn cho người sử dụng. Độ chênh lệch nhiệt độ của nước đầu ra so với đầu vào phụ thuộc vào lưu lượng nước đi qua buồng đốt. Khi nước chảy qua buồng đốt với lưu lượng $5.10^{-2} \mathrm{~kg} / \mathrm{s}$ thì độ chênh lệch nhiệt độ đầu ra so với đầu vào là $20^{\circ} \mathrm{C}$. Cho nhiệt dung riêng của nước là $4200 \mathrm{~J} /(\mathrm{kg} . \mathrm{K})$.
Câu 3 Nhiệt độ của nước đã tăng bao nhiêu Kelvin khi đi qua buồng đốt?
A. 293 K .
B. 261 K .
C. 20 K .
D. 10 K .
Câu 4 Nhiệt lượng mà nước nhận được trong mỗi giờ là
A. 15120 kJ .
B. 9072 kJ .
C. 2856 kJ .
D. 61530 J .
Câu 5 Người ta đổ vào bình cách nhiệt một dung dịch cà phê ở nhiệt độ $\mathrm{t}_1=85^{\circ} \mathrm{C}$ và thả vào đó cục nước đá nhiệt độ $\mathrm{t}_2=0^{\circ} \mathrm{C}$. Khi nước đá tan hết, nhiệt độ của dung dịch cà phê là $\mathrm{t}=40^{\circ} \mathrm{C}$. Giả sử chỉ có sự trao đổi nhiệt giữa dung dịch cà phê với cục nước đá. Biết nhiệt dung riêng của dung dịch cà phê và nước lần lượt là $c_1=4000 \frac{\mathrm{~J}}{\mathrm{~kg} . \mathrm{K}}$ và $\mathrm{c}_2=4200 \frac{\mathrm{~J}}{\mathrm{~kg} . \mathrm{K}}$; nhiệt nóng chảy riêng của nước đá là $\lambda=334 \frac{\mathrm{~kJ}}{\mathrm{~kg}}$. Nồng độ cà phê trong dung dịch (tỉ số khối lượng cà phê và khối lượng dung dịch) sau khi nước đá tan hết giảm so với lúc đầu là
A. $25 \%$.
B. $26,4 \%$.
C. $30 \%$.
D. $47 \%$.
Câu 6 Hai bình cầu cùng dung tích chứa cùng một chất khí nối với nhau bằng một ống nằm ngang. Một giọt thủy ngân nằm đúng giữa ống ngang. Nhiệt độ trong các bình tương ứng là $T_1$ và $T_2$. Tăng gấp đôi nhiệt độ tuyệt đối của khí trong mỗi bình thì giọt thủy ngân sẽ như thế nào?
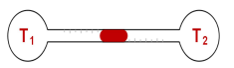
A. Chuyển động sang trái.
B. Chuyển động sang phải.
C. Nằm yên không chuyển động.
D. Chuyển động sang phía có nhiệt độ lớn hon.
Câu 7 Làm biến đổi một lượng khí từ trạng thái 1 sang trạng thái 2 , biết rằng ở trạng thái 2 cả áp suất và thể tích của lượng khí đều lớn hơn ở trạng thái 1 . Trong nhũng cách làm biến đổi lượng khí sau đây, cách nào lượng khí sinh công nhiều nhất?

A. Đun nóng khí đẳng tích rồi đun nóng đẳng áp.
B. Đun nóng khí đẳng áp rồi đun nóng đẳng tích.
C. Đun nóng khí sao cho cả nhiệt độ và áp suất của khí đều tăng đồng thời và liên tục từ trạng thái 1 đến trạng thái 2 .
D. Tương tự như C nhưng theo một dãy biến đổi trạng thái khác C
Câu 8 Hai bình có dung tích bằng nhau chứa cùng một loại khí. Khối lượng của khí lần lượt là m và m'. Ta có đồ thị như hình vẽ. Nhận xét nào sau đây là đúng?

A. m′ > m.
B. m′ ≤ m.
C. m′ < m.
D. m = m′.
Câu 9 Một vòng dây đặt cố định trong từ trường đều như hình vẽ. Khi độ lớn cảm ứng từ B giảm thì phát biểu nào sau đây về dòng điện cảm ứng là đúng?
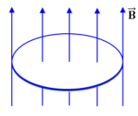
A. Không có dòng diện cảm ưng trong khung dây.
B. Dòng điện cảm ứng chạy theo chiều kim đồng hồ.
C. Dòng điện cảm ứng chạy theo ngược chiều kim đồng hồ.
D. Dòng điện cảm ứng đổi chiều liên tục
Câu 10 Hoạt động của máy biến áp dựa trên
A. Hiện tượng tự cảm
B. Hiện tượng cảm ứng điện từ
C. Từ trường quay
D. Tác dụng của lực từ
Câu 11 Từ thông qua một vòng dây dẫn là $\Phi=\frac{2.10^{-2}}{\pi} \cos \left(100 \pi t-\frac{\pi}{4}\right)(\mathrm{Wb})$. Biểu thức của suất diện động cảm ứng xuất hiện trong vòng dây là
A. $e=2 \cos \left(100 \pi \mathrm{t}+\frac{\pi}{4}\right)(V)$.
B. $e=2 \cos \left(100 \pi \mathrm{t}-\frac{\pi}{4}\right)(V)$.
C. $e=2 \cos (100 \pi \mathrm{t})(V)$.
D. $e=2 \cos \left(100 \pi \mathrm{t}-\frac{3 \pi}{4}\right)(V)$.
Câu 12 Một dây dẫn thẳng có chiều dài $3,0 \mathrm{~m}$ mang dòng điện $6,0 \mathrm{~A}$ được đặt nằm ngang, hướng của dòng điện tạo với hướng Tây một góc $50^{\circ}$ lệch về phía Nam. Trong vùng này, cảm ứng từ của từ trường Trái Đất coi là đều, có độ lớn là $2 \cdot 10^{-5} \mathrm{~T}$ và hướng về phía Bắc. Lực từ tác dụng lên đoạn dây dẫn trên có độ lớn xấp xỉ bằng
A. $2,8 \cdot 10^{-4} \mathrm{~N}$.
B. $2,3.10^{-4} \mathrm{~N}$.
C. $1,9.10^{-4} \mathrm{~N}$.
D. $3,6 \cdot 10^{-4} \mathrm{~N}$.
Câu 13 Đồ thị li độ theo thời gian của hiệu điện thế và cường độ dòng điện có cùng tần số được cho như hình vẽ bên. Độ lệch pha dao động của i so với $u$ là
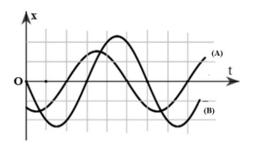
A. $-\frac{\pi}{6} \mathrm{rad}$.
B. $\frac{\pi}{6} \mathrm{rad}$.
C. $\frac{\pi}{3} \mathrm{rad}$.
D. $-\frac{\pi}{3} \mathrm{rad}$.
Câu 14 Độ bền vững của hạt nhân càng cao khi
A. số nucleon của hạt nhân càng nhó.
B. số nucleon của hạt nhân càng lớn.
C. năng lượng liên kết của hạt nhân càng lón.
D. năng lượng liên kết riêng của hạt nhân càng lớn.
Câu 15 Phát biểu nào sau đây là sai khi nói về độ phóng xạ?
A. Độ phóng xạ là đại lượng đặc trưng cho tính phóng xạ mạnh hay yếu của một lượng chất phóng xạ.
B. Đơn vị đo độ phóng xạ là becorren.
C. Với mỗi lượng chất phóng xạ xác định thì độ phóng xạ tỉ lệ với số nguyên tử của lượng chất đó.
D. Độ phóng xạ của một lượng chất phóng xạ phụ thuộc nhiệt độ của lượng chất đó.
Câu 16 Một lượng chất phóng xạ có số lượng hạt nhân ban đầu là $N_o$ sau 3 chu kì bán rã, số lượng hạt nhân phóng xạ còn lại là
A. $N_o / 3$
B. $N_o / 9$
C. $N_o / 8$
D. $\frac{N_o}{\sqrt{3}}$
Câu 17 Một tàu ngầm có công suất 160 kW , dùng năng lượng phân hạch của hạt nhân ${ }^{235} U$ với hiệu suất $20 \%$. Trung bình mỗi hạt ${ }^{235} U$ phân hạch tỏa ra năng lượng 200 MeV . Hỏi sau bao lâu tiêu thụ hết $0,5 \mathrm{~kg}{ }^{235} U$ nguyên chất? Biết $1 \mathrm{MeV}=1,6 \cdot 10^{-13} \mathrm{~J}$
A. 592 ngày.
B. 593 ngày.
C. 594 ngày.
D. 595 ngày
Câu 18 Chất phóng xạ $X$ phân rã theo phương trình $X \rightarrow \alpha+Y$. Số hạt nhân $X\left(N_X\right)$ và số hạt nhân $Y\left(N_Y\right)$ trong mẫu chất đó theo thời gian được mô tả như đồ thị trong hình 3 . Chu kì bán rã của hạt nhân X là bao nhiêu ngày?
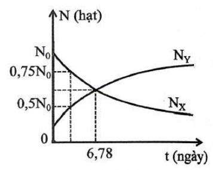
A. 9 ngày.
B. 10 ngày.
C. 11 ngày.
D. 8 ngày
PHẦN II. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 Đổ 1,5 lít nước ở $20^{\circ} \mathrm{C}$ vào một ấm nhôm có khối lượng 600 gam và sau đó đun bằng bếp điện. Sau 40 phút thì đã có $30 \%$ khối lượng nước đã hóa hơi ở nhiệt độ sôi $100^{\circ} \mathrm{C}$. Biết rằng $75 \%$ nhiệt lượng mà bếp cung cấp được dùng vào việc đun nước. Cho biết nhiệt dung riêng của nước là $4190 \mathrm{~J} / \mathrm{kg} . \mathrm{K}$, của nhôm là $880 \mathrm{~J} / \mathrm{kg} . \mathrm{K}$, nhiệt hóa hơi riêng của nước ở $100^{\circ} \mathrm{C}$ là $2,26.10^6 \mathrm{~J} / \mathrm{kg}$, khối lượng riêng của nước là $1 \mathrm{~kg} / \ell$.
a) Âm nhôm và nước trong ấm nhận nhiệt lượng.
b) Nhiệt lượng cần cung cấp cho nước và ấm nhôm làm tròn đến hàng phần trăm bằng $1,56 \mathrm{~kJ}$.
c) Điện năng cần cung cấp cho ấm làm tròn đến hàng phần trăm bằng $2,08 \mathrm{~kJ}$.
d) Công suất cung cấp nhiệt làm tròn đến hàng đơn vị bằng 868 W .
Câu 2 Một chiếc ghế của thợ cắt tóc nâng hạ bằng khí thông qua chuyển động lên xuống của xilanh nối với mặt ghế, thanh nén khí cố định trên đế bịt kín một lượng khí lí tưởng trong xilanh. Bỏ qua ma sát giữa thanh nén và xilanh. Tổng khối lượng của mặt ghế và xilanh là 5 kg , tiết diện của thanh nén là $50 \mathrm{~cm}^2$. Một học sinh nặng 55 kg ngồi lên ghế (hai chân để lơ lửng không chạm mặt sàn) thì ghế hạ xuống 8 cm khi ổn định. Coi nhiệt độ của khí trong xilanh không đổi, áp suất khí quyển là $10^5 \mathrm{~Pa}$ và $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$.
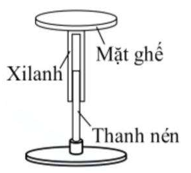
a) Khi ghế để trống, áp suất của khí trong xilanh bằng áp suất khí quyển.
b) Khi học sinh ngồi trên ghế, áp suất của khí trong xilanh là $2,2 \cdot 10^5 \mathrm{~Pa}$.
c) Quá trình ghế hạ xuống, khí trong xilanh thực hiện công.
d) Khi ghế để trống, cột khí trong xilanh dài là 16 cm .
Câu 3 Một mol khí lí tuởng thực hiện chu trình biến đổi được biểu diễn bằng đồ thị như hình vẽ. Cho $T(K)=t^{\circ} \mathrm{C}+273$.
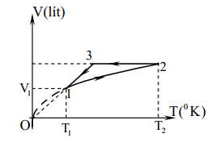
+ Từ 1-2: là một phần của nhánh Parabol có đỉnh tại gốc tọa độ O (phương trình Parabol này có dạng $\mathrm{T}=\mathrm{a}^2$, $\mathrm{a}\left(\mathrm{K} / \mathrm{m}^6\right)$ là hằng số)
+ Từ 2-3: là một đoạn thẳng có đường kéo dài vuông góc với trục OV
+ Từ 3-1: là một đoạn thẳng có đường kéo dài đi qua gốc tọa độ O . Cho biết: $\mathrm{p}_1=8,31.10^5 \mathrm{~Pa}$; $\mathrm{t}_1=27^{\circ} \mathrm{C} ; \mathrm{p}_2=13,85.10^5 \mathrm{~Pa} ; \mathrm{R}=8,31 \mathrm{~J} / \mathrm{mol} . \mathrm{K}$.
a) đường $3-1$ biểu diễn quá trình đẳng áp.
b) giá trị của a làm tròn đến chữ số hàng đơn vị bằng 33 .
c) nhiệt độ $\mathrm{T}_2$ ở trạng thái 2 làm tròn đến hàng phần mười bằng $833,3 \mathrm{~K}$
d) Công khối khí thực hiện được khi biến đổi trạng thái từ 1 đến 2 bằng 2216 J
Câu 4 Chất phóng xạ̣ ${ }_{11}^{25} \mathrm{Na}$ là một chất phóng xạ có chu kì bán rã là 62 giây. Ban đầu mẫu ${ }_{11}^{25} \mathrm{Na}$ có khối lượng $0,248 \mathrm{mg}$. Lấy số Avôgađrô $\mathrm{N}_{\mathrm{A}}=6,02 \cdot 10^{23}$ hạt $/ \mathrm{mol}$.
a) Công thức tính độ phóng xạ là $H_t=\lambda N_t$.
b) Cứ sau một khoảng thời gian là 62 s thì một nửa số hạt Na hiện có bị phân rã.
c) Độ phóng xạ của mẫu trên sau 10 phút là $8,15 \cdot 10^{16} \mathrm{~Bq}$.
d) Sau 186 giây thì độ phóng xạ của mẫu trên chỉ còn bằng $12,5 \%$ độ phóng xạ ban đầu.
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6 .
Sử dụng các thông tin sau cho Câu 1 và Câu 2: Để khảo sát dòng điện do máy phát điện xoay chiều một pha tạo ra ta nối hai cực của máy phát với một dao động ký như hình 1 . Hình 2 là ảnh chụp lại từ màn hình của dao động ký là đồ thị biểu diễn sự phụ thuộc của cường độ dòng điện qua dao động ký theo thời gian. Biết ứng với mỗi ô vuông cạnh nằm ngang tương ứng thời gian $0,004 \mathrm{~s} ;$ mỗi ô cạnh đứng tương ứng $1,0 \mathrm{~A}$
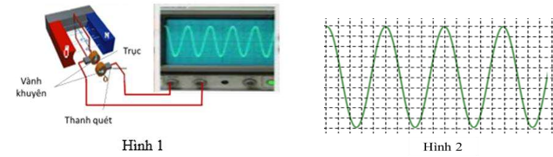
Câu 1 Tần số dòng diện do máy phát tạo ra là bao nhiêu Hertz?
Câu 2 Cường độ dòng điện hiệu dụng qua dao động ký bằng bao nhiêu Ampe? (làm tròn đến chữ số hàng phần mười)
Câu 3 Nhiệt lượng mà trà toả ra môi trường trong 2 s là bao nhiêu Jun? (Kết quả làm tròn đến chữ số hàng đon vị)
Câu 4 Nhiệt độ của trà sau khi rót vào cốc 30 s đã thay đổi bao nhiêu độ Celsius? (Kết quả làm tròn đến chữ số hàng phần mười).
Sử dụng các thông tin sau cho Câu 5 và Câu 6: Chất phóng xạ Pôlôni ${ }_{84}^{210}$ Po phóng xạ tia $\alpha$ và biến thành hạt nhân chì Pb . Biết chu kỳ bán rã của ${ }_{84}^{210} \mathrm{Po}$ là 138 ngày và ban đầu có $100 \mathrm{~g}{ }_{84}^{210} \mathrm{Po}$. Lấy khối lượng nguyên tử xấp xỉ số khối $\mathrm{A}(\mathrm{u})$.
Câu 5 Số hạt nucleon của 1 hạt nhân Po là bao nhiêu?
Câu 6 Số hạt Po còn lại sau 69 ngày là $x .10^{22}$ hạt. Giá trị của $x$ là bao nhiêu ? (làm tròn đến chữ số hàng đơn vị)
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 18. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 Câu nào sau đây nói về truyền nhiệt và thực hiện công là không đúng?
A. Thực hiện công là quá trình có thể làm thay đổi nội năng của vật.
B. Truyền nhiệt là quá trình có thể làm thay đổi nội năng của vật.
C. Trong thực hiện công có sự chuyển hoá năng lượng.
D. Trong truyền nhiệt có sự chuyển hoá năng lượng.
Chọn D
A. 6 g .
B. $1,2 \mathrm{~g}$.
C. 6 kg .
D. $1,2 \mathrm{~kg}$.
$\begin{array}{l} Q = 0,2{m_0}\lambda \\ \Rightarrow 396 \cdot {10^3} = 0,2{m_0} \cdot 3,3 \cdot {10^5}\\ \Rightarrow {m_0} = 6\;{\rm{kg}}.{\rm{ }} \end{array}$
chọn C
chọn C
Câu 3 Nhiệt độ của nước đã tăng bao nhiêu Kelvin khi đi qua buồng đốt?
A. 293 K .
B. 261 K .
C. 20 K .
D. 10 K .
$\Delta T(K)=\Delta t\left({ }^{\circ} C\right)=20$. Chọn C
A. 15120 kJ .
B. 9072 kJ .
C. 2856 kJ .
D. 61530 J .
$\begin{array}{l} Q = mc\Delta t\\ = 5 \cdot {10^{ - 2}} \cdot 60 \cdot 60 \cdot 4200 \cdot 20\\ = 15120 \cdot {10^3}J\\ = 15120\;{\rm{kJ}}.{\rm{ }} \end{array}$
Chọn A
Chọn A
A. $25 \%$.
B. $26,4 \%$.
C. $30 \%$.
D. $47 \%$.
$\begin{array}{l} {m_1}{c_1}\left( {{t_1} - t} \right) = {m_2}\left( {\lambda + {c_2}t} \right)\\ \Rightarrow {m_1} \cdot 4000 \cdot (85 - 40) = {m_2}\left( {334 \cdot {{10}^3} + 4200 \cdot 40} \right)\\ \Rightarrow {m_2} = \frac{{90}}{{251}}{m_1}\\ \frac{{{C_1} - {C_2}}}{{{C_1}}} = 1 - \frac{{{C_2}}}{{{C_1}}}\\ = 1 - \frac{{\frac{{{m_{cp}}}}{{{m_1} + {m_2}}}}}{{\frac{{{m_{cp}}}}{{{m_1}}}}}\\ = 1 - \frac{{{m_1}}}{{{m_1} + {m_2}}}\\ = 1 - \frac{1}{{1 + \frac{{90}}{{251}}}}\\ \approx 0,264 = 26,4\% {\rm{. }} \end{array}$
Chọn B
Chọn B

A. Chuyển động sang trái.
B. Chuyển động sang phải.
C. Nằm yên không chuyển động.
D. Chuyển động sang phía có nhiệt độ lớn hon.
$\left\{ \begin{array}{*{35}{l}} \frac{pV}{{{T}_{1}}}=\frac{{{p}^{\prime }}{{V}_{1}}}{2{{T}_{1}}} \\ \frac{pV}{{{T}_{2}}}=\frac{{{p}^{\prime }}{{V}_{2}}}{2{{T}_{2}}} \\ \end{array}\Rightarrow pV=\frac{{{p}^{\prime }}{{V}_{1}}}{2}=\frac{{{p}^{\prime }}{{V}_{2}}}{2}\Rightarrow {{V}_{1}}={{V}_{2}}.\text{ } \right.$
Chọn C
Chọn C

A. Đun nóng khí đẳng tích rồi đun nóng đẳng áp.
B. Đun nóng khí đẳng áp rồi đun nóng đẳng tích.
C. Đun nóng khí sao cho cả nhiệt độ và áp suất của khí đều tăng đồng thời và liên tục từ trạng thái 1 đến trạng thái 2 .
D. Tương tự như C nhưng theo một dãy biến đổi trạng thái khác C
Quá trình ở đáp án A có diện tích giới hạn lớn nhất nên công lớn nhất Chọn A

A. m′ > m.
B. m′ ≤ m.
C. m′ < m.
D. m = m′.
$p V=n R T=\frac{m}{M} R T \Rightarrow p=\frac{m R}{M V} \cdot T \Rightarrow$ hệ số góc $\frac{m^{\prime} R}{M V}>\frac{m R}{M V} \Rightarrow m^{\prime}>m$. Chọn A

A. Không có dòng diện cảm ưng trong khung dây.
B. Dòng điện cảm ứng chạy theo chiều kim đồng hồ.
C. Dòng điện cảm ứng chạy theo ngược chiều kim đồng hồ.
D. Dòng điện cảm ứng đổi chiều liên tục
B giảm $\Rightarrow$ từ thông giảm $\Rightarrow \overrightarrow{B_{c u}} \uparrow \uparrow \vec{B} \Rightarrow$ áp dụng quy tắc nắm tay phải được chiều dòng điện cảm ứng chạy theo ngược chiều kim đồng hồ. Chọn C
A. Hiện tượng tự cảm
B. Hiện tượng cảm ứng điện từ
C. Từ trường quay
D. Tác dụng của lực từ
Chọn B
A. $e=2 \cos \left(100 \pi \mathrm{t}+\frac{\pi}{4}\right)(V)$.
B. $e=2 \cos \left(100 \pi \mathrm{t}-\frac{\pi}{4}\right)(V)$.
C. $e=2 \cos (100 \pi \mathrm{t})(V)$.
D. $e=2 \cos \left(100 \pi \mathrm{t}-\frac{3 \pi}{4}\right)(V)$.
$\varphi_e=\varphi_\phi-\frac{\pi}{2}=-\frac{\pi}{4}-\frac{\pi}{2}=-\frac{3 \pi}{4}$. Chọn D
A. $2,8 \cdot 10^{-4} \mathrm{~N}$.
B. $2,3.10^{-4} \mathrm{~N}$.
C. $1,9.10^{-4} \mathrm{~N}$.
D. $3,6 \cdot 10^{-4} \mathrm{~N}$.
$\begin{array}{l} F = ilB\sin \alpha \\ = 6 \cdot 3 \cdot 2 \cdot {10^{ - 5}} \cdot \sin \left( {{{90}^0} + {{50}^0}} \right)\\ \approx 2,3 \cdot {10^{ - 4}}N \end{array}$
. Chọn B
. Chọn B

A. $-\frac{\pi}{6} \mathrm{rad}$.
B. $\frac{\pi}{6} \mathrm{rad}$.
C. $\frac{\pi}{3} \mathrm{rad}$.
D. $-\frac{\pi}{3} \mathrm{rad}$.
3 ô ưng với $\pi \Rightarrow 1$ ô úng với $\pi / 3 \Rightarrow \mathrm{i}$ trễ pha hơn u là $\pi / 3$. Chọn D
A. số nucleon của hạt nhân càng nhó.
B. số nucleon của hạt nhân càng lớn.
C. năng lượng liên kết của hạt nhân càng lón.
D. năng lượng liên kết riêng của hạt nhân càng lớn.
Chọn D
A. Độ phóng xạ là đại lượng đặc trưng cho tính phóng xạ mạnh hay yếu của một lượng chất phóng xạ.
B. Đơn vị đo độ phóng xạ là becorren.
C. Với mỗi lượng chất phóng xạ xác định thì độ phóng xạ tỉ lệ với số nguyên tử của lượng chất đó.
D. Độ phóng xạ của một lượng chất phóng xạ phụ thuộc nhiệt độ của lượng chất đó.
$H=\lambda N$. Chọn D
A. $N_o / 3$
B. $N_o / 9$
C. $N_o / 8$
D. $\frac{N_o}{\sqrt{3}}$
$N=N_0 .2^{\frac{-t}{T}}=N_0 .2^{-3}=\frac{N_0}{8}$. Chọn C
A. 592 ngày.
B. 593 ngày.
C. 594 ngày.
D. 595 ngày
$n=\frac{m}{M}=\frac{0,5 \cdot 10^3}{235}=\frac{100}{47} \mathrm{~mol}$
$N=n N_A=\frac{100}{47} \cdot 6,02 \cdot 10^{23} \approx 1,281.10^{24}$
$Q=N \Delta E=1,281 \cdot 10^{24} \cdot 200 \cdot 1,6 \cdot 10^{-13} \approx 4,1 \cdot 10^{13} J$
$A=H Q=0,2.4,1.10^{13}=8,2.10^{12} J$
$t=\frac{Q}{P}=\frac{8,2.10^{12}}{160.10^3}=5125.10^4 s \approx 593$ ngày. Chọn B
$N=n N_A=\frac{100}{47} \cdot 6,02 \cdot 10^{23} \approx 1,281.10^{24}$
$Q=N \Delta E=1,281 \cdot 10^{24} \cdot 200 \cdot 1,6 \cdot 10^{-13} \approx 4,1 \cdot 10^{13} J$
$A=H Q=0,2.4,1.10^{13}=8,2.10^{12} J$
$t=\frac{Q}{P}=\frac{8,2.10^{12}}{160.10^3}=5125.10^4 s \approx 593$ ngày. Chọn B

A. 9 ngày.
B. 10 ngày.
C. 11 ngày.
D. 8 ngày
$\left\{ \begin{array}{*{35}{l}}
{{N}_{X}}={{N}_{0}}\cdot {{2}^{\frac{-t}{T}}} \\
{{N}_{Y}}={{N}_{0Y}}+{{N}_{0}}\cdot \left( 1-{{2}^{\frac{-t}{T}}} \right)\Rightarrow \left\{ \begin{array}{*{35}{l}}
0,75={{2}^{\frac{-{{t}_{1}}}{T}}} \\
0,5{{N}_{0}}={{N}_{0Y}}+{{N}_{0}}\cdot \left( 1-{{2}^{\frac{-t}{T}}} \right) \\
\end{array} \right. \\
\Rightarrow 0,5{{N}_{0}}={{N}_{0Y}}+{{N}_{0}}\cdot (1-0,75)\Rightarrow {{N}_{0Y}}=0,25{{N}_{0}} \\
\end{array} \right.$
$\begin{align} & \frac{{{N}_{Y}}}{{{N}_{X}}}=\frac{0,25{{N}_{0}}+{{N}_{0}}\cdot \left( 1-{{2}^{\frac{-t}{T}}} \right)}{{{N}_{0}}\cdot {{2}^{\frac{-t}{T}}}} \\ & \Rightarrow 1=\frac{0,25+\left( 1-{{2}^{\frac{-{{t}_{2}}}{T}}} \right)}{{{2}^{\frac{-{{t}_{2}}}{T}}}} \\ & \Rightarrow {{2}^{\frac{-{{t}_{2}}}{T}}}=0,625\xrightarrow{{{t}_{2}}=6,78}TT\approx 10\text{ ng }\!\!\grave{\mathrm{a}}\!\!\text{ y} \\ \end{align}$
Chọn B
{{N}_{X}}={{N}_{0}}\cdot {{2}^{\frac{-t}{T}}} \\
{{N}_{Y}}={{N}_{0Y}}+{{N}_{0}}\cdot \left( 1-{{2}^{\frac{-t}{T}}} \right)\Rightarrow \left\{ \begin{array}{*{35}{l}}
0,75={{2}^{\frac{-{{t}_{1}}}{T}}} \\
0,5{{N}_{0}}={{N}_{0Y}}+{{N}_{0}}\cdot \left( 1-{{2}^{\frac{-t}{T}}} \right) \\
\end{array} \right. \\
\Rightarrow 0,5{{N}_{0}}={{N}_{0Y}}+{{N}_{0}}\cdot (1-0,75)\Rightarrow {{N}_{0Y}}=0,25{{N}_{0}} \\
\end{array} \right.$
$\begin{align} & \frac{{{N}_{Y}}}{{{N}_{X}}}=\frac{0,25{{N}_{0}}+{{N}_{0}}\cdot \left( 1-{{2}^{\frac{-t}{T}}} \right)}{{{N}_{0}}\cdot {{2}^{\frac{-t}{T}}}} \\ & \Rightarrow 1=\frac{0,25+\left( 1-{{2}^{\frac{-{{t}_{2}}}{T}}} \right)}{{{2}^{\frac{-{{t}_{2}}}{T}}}} \\ & \Rightarrow {{2}^{\frac{-{{t}_{2}}}{T}}}=0,625\xrightarrow{{{t}_{2}}=6,78}TT\approx 10\text{ ng }\!\!\grave{\mathrm{a}}\!\!\text{ y} \\ \end{align}$
Chọn B
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 Đổ 1,5 lít nước ở $20^{\circ} \mathrm{C}$ vào một ấm nhôm có khối lượng 600 gam và sau đó đun bằng bếp điện. Sau 40 phút thì đã có $30 \%$ khối lượng nước đã hóa hơi ở nhiệt độ sôi $100^{\circ} \mathrm{C}$. Biết rằng $75 \%$ nhiệt lượng mà bếp cung cấp được dùng vào việc đun nước. Cho biết nhiệt dung riêng của nước là $4190 \mathrm{~J} / \mathrm{kg} . \mathrm{K}$, của nhôm là $880 \mathrm{~J} / \mathrm{kg} . \mathrm{K}$, nhiệt hóa hơi riêng của nước ở $100^{\circ} \mathrm{C}$ là $2,26.10^6 \mathrm{~J} / \mathrm{kg}$, khối lượng riêng của nước là $1 \mathrm{~kg} / \ell$.
a) Âm nhôm và nước trong ấm nhận nhiệt lượng.
b) Nhiệt lượng cần cung cấp cho nước và ấm nhôm làm tròn đến hàng phần trăm bằng $1,56 \mathrm{~kJ}$.
c) Điện năng cần cung cấp cho ấm làm tròn đến hàng phần trăm bằng $2,08 \mathrm{~kJ}$.
d) Công suất cung cấp nhiệt làm tròn đến hàng đơn vị bằng 868 W .
$m_n=V D=1,5.1=1,5 \mathrm{~kg}$
$\begin{array}{l} Q = \left( {{m_n}{c_n} + {m_{nh}}{c_{nh}}} \right)\Delta t + 0,3{m_n}L\\ = (1,5 \cdot 4190 + 0,6 \cdot 880) \cdot (100 - 20) + 0,3 \cdot 1,5 \cdot 2,26 \cdot {10^6}\\ = 1562040J \end{array}$
$A=\frac{Q}{H}=\frac{1562040}{0,75}=2082720 \mathrm{~J}$
$P=\frac{A}{t}=\frac{2082720}{40.60}=867,8 \mathrm{~W} \Rightarrow$ a) Đúng; b) Sai; c) Sai; d) Đúng
$\begin{array}{l} Q = \left( {{m_n}{c_n} + {m_{nh}}{c_{nh}}} \right)\Delta t + 0,3{m_n}L\\ = (1,5 \cdot 4190 + 0,6 \cdot 880) \cdot (100 - 20) + 0,3 \cdot 1,5 \cdot 2,26 \cdot {10^6}\\ = 1562040J \end{array}$
$A=\frac{Q}{H}=\frac{1562040}{0,75}=2082720 \mathrm{~J}$
$P=\frac{A}{t}=\frac{2082720}{40.60}=867,8 \mathrm{~W} \Rightarrow$ a) Đúng; b) Sai; c) Sai; d) Đúng

a) Khi ghế để trống, áp suất của khí trong xilanh bằng áp suất khí quyển.
b) Khi học sinh ngồi trên ghế, áp suất của khí trong xilanh là $2,2 \cdot 10^5 \mathrm{~Pa}$.
c) Quá trình ghế hạ xuống, khí trong xilanh thực hiện công.
d) Khi ghế để trống, cột khí trong xilanh dài là 16 cm .
$\begin{array}{l} {p_1} = {p_0} + \frac{{{m_{gh}}g}}{S}\\ = {10^5} + \frac{{5 \cdot 10}}{{50 \cdot {{10}^{ - 4}}}}\\ = 1,1 \cdot {10^5}\;{\rm{Pa}} \end{array}$
a) Sai
$\begin{array}{l} {p_2} = {p_0} + \frac{{\left( {{m_{hs}} + {m_{gh}}} \right)g}}{S}\\ = {10^5} + \frac{{(55 + 5) \cdot 10}}{{50 \cdot {{10}^{ - 4}}}}\\ = 2,2 \cdot {10^5}Pa \end{array}$
b) Đúng
Quá trình ghế hạ xuống, khí trong xilanh nhận công $\Rightarrow $ c) Sai
$p V=$ const
$\begin{array}{l} \Rightarrow {p_1} \cdot Sl = {p_2} \cdot S(l - 8)\\ \Rightarrow 1,1 \cdot {10^5}.l = 2,2 \cdot {10^5}.(l - 8)\\ \Rightarrow l = 16\;{\rm{cm}} \end{array}$
d) Đúng
a) Sai
$\begin{array}{l} {p_2} = {p_0} + \frac{{\left( {{m_{hs}} + {m_{gh}}} \right)g}}{S}\\ = {10^5} + \frac{{(55 + 5) \cdot 10}}{{50 \cdot {{10}^{ - 4}}}}\\ = 2,2 \cdot {10^5}Pa \end{array}$
b) Đúng
Quá trình ghế hạ xuống, khí trong xilanh nhận công $\Rightarrow $ c) Sai
$p V=$ const
$\begin{array}{l} \Rightarrow {p_1} \cdot Sl = {p_2} \cdot S(l - 8)\\ \Rightarrow 1,1 \cdot {10^5}.l = 2,2 \cdot {10^5}.(l - 8)\\ \Rightarrow l = 16\;{\rm{cm}} \end{array}$
d) Đúng

+ Từ 1-2: là một phần của nhánh Parabol có đỉnh tại gốc tọa độ O (phương trình Parabol này có dạng $\mathrm{T}=\mathrm{a}^2$, $\mathrm{a}\left(\mathrm{K} / \mathrm{m}^6\right)$ là hằng số)
+ Từ 2-3: là một đoạn thẳng có đường kéo dài vuông góc với trục OV
+ Từ 3-1: là một đoạn thẳng có đường kéo dài đi qua gốc tọa độ O . Cho biết: $\mathrm{p}_1=8,31.10^5 \mathrm{~Pa}$; $\mathrm{t}_1=27^{\circ} \mathrm{C} ; \mathrm{p}_2=13,85.10^5 \mathrm{~Pa} ; \mathrm{R}=8,31 \mathrm{~J} / \mathrm{mol} . \mathrm{K}$.
a) đường $3-1$ biểu diễn quá trình đẳng áp.
b) giá trị của a làm tròn đến chữ số hàng đơn vị bằng 33 .
c) nhiệt độ $\mathrm{T}_2$ ở trạng thái 2 làm tròn đến hàng phần mười bằng $833,3 \mathrm{~K}$
d) Công khối khí thực hiện được khi biến đổi trạng thái từ 1 đến 2 bằng 2216 J
a) Đúng
$\begin{array}{l} \frac{{{p_1}{V_1}}}{{{T_1}}} = nR\\ \Rightarrow \frac{{8,31 \cdot {{10}^5} \cdot {V_1}}}{{27 + 273}} = 8,31\\ \Rightarrow {V_1} = 3 \cdot {10^{ - 3}}\;{{\rm{m}}^3} \end{array}$
$\begin{array}{l} {T_1} = aV_1^2\\ \Rightarrow 27 + 273 = a \cdot {\left( {3 \cdot {{10}^{ - 3}}} \right)^2}\\ \Rightarrow a = \frac{{10}}{3} \cdot {10^7}\left( {\;{\rm{K}}/{{\rm{m}}^6}} \right) \end{array}$
b) Sai
$\begin{array}{l} \frac{{{p_2}{V_2}}}{{{T_2}}} = nR\\ \Rightarrow \frac{{13,85 \cdot {{10}^5} \cdot {V_2}}}{{\frac{{10}}{3} \cdot {{10}^7} \cdot V_2^2}} = 8,31\\ \Rightarrow {V_2} = 5 \cdot {10^{ - 3}}\;{{\rm{m}}^3}\\ \Rightarrow {T_2} = 833,3\;{\rm{K}} \end{array}$
c) Đúng
Từ 1 đến 2 có $n R=\frac{p V}{T}=\frac{p V}{a V^2}=\frac{p}{a V} \Rightarrow p=n R a V \Rightarrow \mathrm{p}$ theo V là hàm bậc nhất
$\begin{array}{l} A_{12}^, = \frac{1}{2}\left( {{p_1} + {p_2}} \right)\left( {{V_2} - {V_1}} \right)\\ = \frac{1}{2}\left( {8,31 \cdot {{10}^5} + 13,85 \cdot {{10}^5}} \right)(5 - 3) \cdot {10^{ - 3}}\\ = 2216J \end{array}$
d) Đúng
$\begin{array}{l} \frac{{{p_1}{V_1}}}{{{T_1}}} = nR\\ \Rightarrow \frac{{8,31 \cdot {{10}^5} \cdot {V_1}}}{{27 + 273}} = 8,31\\ \Rightarrow {V_1} = 3 \cdot {10^{ - 3}}\;{{\rm{m}}^3} \end{array}$
$\begin{array}{l} {T_1} = aV_1^2\\ \Rightarrow 27 + 273 = a \cdot {\left( {3 \cdot {{10}^{ - 3}}} \right)^2}\\ \Rightarrow a = \frac{{10}}{3} \cdot {10^7}\left( {\;{\rm{K}}/{{\rm{m}}^6}} \right) \end{array}$
b) Sai
$\begin{array}{l} \frac{{{p_2}{V_2}}}{{{T_2}}} = nR\\ \Rightarrow \frac{{13,85 \cdot {{10}^5} \cdot {V_2}}}{{\frac{{10}}{3} \cdot {{10}^7} \cdot V_2^2}} = 8,31\\ \Rightarrow {V_2} = 5 \cdot {10^{ - 3}}\;{{\rm{m}}^3}\\ \Rightarrow {T_2} = 833,3\;{\rm{K}} \end{array}$
c) Đúng
Từ 1 đến 2 có $n R=\frac{p V}{T}=\frac{p V}{a V^2}=\frac{p}{a V} \Rightarrow p=n R a V \Rightarrow \mathrm{p}$ theo V là hàm bậc nhất
$\begin{array}{l} A_{12}^, = \frac{1}{2}\left( {{p_1} + {p_2}} \right)\left( {{V_2} - {V_1}} \right)\\ = \frac{1}{2}\left( {8,31 \cdot {{10}^5} + 13,85 \cdot {{10}^5}} \right)(5 - 3) \cdot {10^{ - 3}}\\ = 2216J \end{array}$
d) Đúng
a) Công thức tính độ phóng xạ là $H_t=\lambda N_t$.
b) Cứ sau một khoảng thời gian là 62 s thì một nửa số hạt Na hiện có bị phân rã.
c) Độ phóng xạ của mẫu trên sau 10 phút là $8,15 \cdot 10^{16} \mathrm{~Bq}$.
d) Sau 186 giây thì độ phóng xạ của mẫu trên chỉ còn bằng $12,5 \%$ độ phóng xạ ban đầu.
a) Đúng
b) Đúng. Sau 1T thì một nửa số hạt Na hiện có bị phân rã.
c) Sai. $n_0=\frac{m}{M}=\frac{0,248 \cdot 10^{-3}}{25}=9,92 \cdot 10^{-6} \mathrm{~mol}$
$\begin{array}{l} {N_0} = {n_0}{N_A} = \\ 9,92 \cdot {10^{ - 6}} \cdot 6,02 \cdot {10^{23}}\\ \approx 5,972 \cdot {10^{18}}\\ H = \lambda N\\ = \frac{{\ln 2}}{T} \cdot {N_0} \cdot {2^{\frac{{ - t}}{T}}}\\ = \frac{{\ln 2}}{{62}} \cdot 5,972 \cdot {10^{18}} \cdot {2^{\frac{{ - 10.60}}{{62}}}}\\ \approx 8,15 \cdot {10^{15}}\;{\rm{Bq}} \end{array}$
d) Đúng. $\frac{H}{{{H}_{0}}}={{2}^{\frac{-t}{T}}}={{2}^{\frac{-186}{62}}}=0,125=12,5%$
b) Đúng. Sau 1T thì một nửa số hạt Na hiện có bị phân rã.
c) Sai. $n_0=\frac{m}{M}=\frac{0,248 \cdot 10^{-3}}{25}=9,92 \cdot 10^{-6} \mathrm{~mol}$
$\begin{array}{l} {N_0} = {n_0}{N_A} = \\ 9,92 \cdot {10^{ - 6}} \cdot 6,02 \cdot {10^{23}}\\ \approx 5,972 \cdot {10^{18}}\\ H = \lambda N\\ = \frac{{\ln 2}}{T} \cdot {N_0} \cdot {2^{\frac{{ - t}}{T}}}\\ = \frac{{\ln 2}}{{62}} \cdot 5,972 \cdot {10^{18}} \cdot {2^{\frac{{ - 10.60}}{{62}}}}\\ \approx 8,15 \cdot {10^{15}}\;{\rm{Bq}} \end{array}$
d) Đúng. $\frac{H}{{{H}_{0}}}={{2}^{\frac{-t}{T}}}={{2}^{\frac{-186}{62}}}=0,125=12,5%$
Thí sinh trả lời từ câu 1 đến câu 6 .
Sử dụng các thông tin sau cho Câu 1 và Câu 2: Để khảo sát dòng điện do máy phát điện xoay chiều một pha tạo ra ta nối hai cực của máy phát với một dao động ký như hình 1 . Hình 2 là ảnh chụp lại từ màn hình của dao động ký là đồ thị biểu diễn sự phụ thuộc của cường độ dòng điện qua dao động ký theo thời gian. Biết ứng với mỗi ô vuông cạnh nằm ngang tương ứng thời gian $0,004 \mathrm{~s} ;$ mỗi ô cạnh đứng tương ứng $1,0 \mathrm{~A}$

Câu 1 Tần số dòng diện do máy phát tạo ra là bao nhiêu Hertz?
$T=5\hat{o}=5.0,004=0,02s\Rightarrow f=\frac{1}{T}=50~\text{Hz}$
Trả lời ngắn: 50
Trả lời ngắn: 50
${{I}_{0}}=5\hat{o}=5A\Rightarrow I=\frac{{{I}_{0}}}{\sqrt{2}}\approx 3,5A$
Trả lời ngắn: 3,5
Sử dụng các thông tin sau cho Câu 3 và Câu 4: Diễn viên Angelina NgocMinh là một người uống trà sành điệu. Cô ấy pha chế một loại trà mới bằng nước sôi trong một chiếc cốc hình trụ có bán kính trong $\mathrm{r}=4 \mathrm{~cm}$ và chiều cao $\mathrm{h}=10 \mathrm{~cm}$. Cốc của cô ấy có nắp đậy để giữ nhiệt tốt hơn. Trong khoảng thời gian ngắn $\Delta \tau(\mathrm{s})$ lượng nhiệt mà trà tỏa ra môi trường cho bởi công thức $\Delta \mathrm{Q}=\frac{k S\left(t_t-t_p\right)}{d} \Delta \tau$, biết $\mathrm{S}\left(\mathrm{m}^2\right)$ là diện tích mặt trong của cốc, nhiệt độ phòng $\mathrm{t}_{\mathrm{p}}$, nhiệt độ của trà là $t_t$ và $\mathrm{d}=5 \mathrm{~mm}$ là chiều dày của thành cốc. Khi nhiệt bị mất đi, nhiệt độ của trà thay đổi một lượng $\Delta \mathrm{T}$ cho bởi $\Delta Q=c m \Delta T$ trong đó, m là khối lượng của nước và các số liệu như sau: Nhiệt độ sôi của nước $\mathrm{t}_{\mathrm{s}}=100^{\circ} \mathrm{C}$; độ dẫn nhiệt của cốc $\mathrm{k}=1,0 \mathrm{Wm}^{-1} \mathrm{~K}^{-1}$; nhiệt độ phòng $\mathrm{t}_{\mathrm{p}}=25^{\circ} \mathrm{C}$; Khối lượng riêng của nước $\rho=1000 \mathrm{~kg} / \mathrm{m}^3$; Nhiệt dung riêng của nước $\mathrm{C}=4180 \mathrm{~J}$. $\mathrm{kg}^{-1} \mathrm{~K}^{-1}$. Angelina NgocMinh rót trà đầy cốc và ngay lập tức đậy kín nắp.
Trả lời ngắn: 3,5
Sử dụng các thông tin sau cho Câu 3 và Câu 4: Diễn viên Angelina NgocMinh là một người uống trà sành điệu. Cô ấy pha chế một loại trà mới bằng nước sôi trong một chiếc cốc hình trụ có bán kính trong $\mathrm{r}=4 \mathrm{~cm}$ và chiều cao $\mathrm{h}=10 \mathrm{~cm}$. Cốc của cô ấy có nắp đậy để giữ nhiệt tốt hơn. Trong khoảng thời gian ngắn $\Delta \tau(\mathrm{s})$ lượng nhiệt mà trà tỏa ra môi trường cho bởi công thức $\Delta \mathrm{Q}=\frac{k S\left(t_t-t_p\right)}{d} \Delta \tau$, biết $\mathrm{S}\left(\mathrm{m}^2\right)$ là diện tích mặt trong của cốc, nhiệt độ phòng $\mathrm{t}_{\mathrm{p}}$, nhiệt độ của trà là $t_t$ và $\mathrm{d}=5 \mathrm{~mm}$ là chiều dày của thành cốc. Khi nhiệt bị mất đi, nhiệt độ của trà thay đổi một lượng $\Delta \mathrm{T}$ cho bởi $\Delta Q=c m \Delta T$ trong đó, m là khối lượng của nước và các số liệu như sau: Nhiệt độ sôi của nước $\mathrm{t}_{\mathrm{s}}=100^{\circ} \mathrm{C}$; độ dẫn nhiệt của cốc $\mathrm{k}=1,0 \mathrm{Wm}^{-1} \mathrm{~K}^{-1}$; nhiệt độ phòng $\mathrm{t}_{\mathrm{p}}=25^{\circ} \mathrm{C}$; Khối lượng riêng của nước $\rho=1000 \mathrm{~kg} / \mathrm{m}^3$; Nhiệt dung riêng của nước $\mathrm{C}=4180 \mathrm{~J}$. $\mathrm{kg}^{-1} \mathrm{~K}^{-1}$. Angelina NgocMinh rót trà đầy cốc và ngay lập tức đậy kín nắp.
$\begin{array}{l} S = \pi {r^2} + 2\pi rh\\ = \pi \cdot {4^2} + 2\pi \cdot 4 \cdot 10 = 96\pi \left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\\ V = \pi {r^2}h\\ = \pi \cdot {4^2} \cdot 10 = 160\pi \left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\\ m = VD\\ = 160\pi \cdot {10^{ - 6}} \cdot 1000 = 0,16\pi (\;{\rm{kg}}) \end{array}$
$\begin{array}{l} - mc \cdot d{t_t} = \frac{{kS\left( {{t_t} - {t_p}} \right)}}{d} \cdot d\tau \\ \Rightarrow - \frac{1}{{{t_t} - {t_p}}} \cdot d{t_t} = \frac{{kS}}{{mcd}} \cdot d\tau \\ \Rightarrow - \int_{100}^4 {\frac{1}{{{t_t} - 25}}} \cdot d{t_t} = \int_0^2 {\frac{{96\pi \cdot {{10}^{ - 4}}}}{{0,16\pi \cdot 4180 \cdot 5 \cdot {{10}^{ - 3}}}}} \cdot d\tau \end{array}$
Casio shift solve $\Rightarrow t_t \approx 99,5706^{\circ} \mathrm{C}$
$\begin{array}{l} Q = mc\Delta T\\ = 0,16\pi \cdot 4180.(100 - 99,5706)\\ \approx 902J \end{array}$
Trả lời ngắn: 902
$\begin{array}{l} - mc \cdot d{t_t} = \frac{{kS\left( {{t_t} - {t_p}} \right)}}{d} \cdot d\tau \\ \Rightarrow - \frac{1}{{{t_t} - {t_p}}} \cdot d{t_t} = \frac{{kS}}{{mcd}} \cdot d\tau \\ \Rightarrow - \int_{100}^4 {\frac{1}{{{t_t} - 25}}} \cdot d{t_t} = \int_0^2 {\frac{{96\pi \cdot {{10}^{ - 4}}}}{{0,16\pi \cdot 4180 \cdot 5 \cdot {{10}^{ - 3}}}}} \cdot d\tau \end{array}$
Casio shift solve $\Rightarrow t_t \approx 99,5706^{\circ} \mathrm{C}$
$\begin{array}{l} Q = mc\Delta T\\ = 0,16\pi \cdot 4180.(100 - 99,5706)\\ \approx 902J \end{array}$
Trả lời ngắn: 902
$\begin{array}{l} - mc \cdot d{t_t} = \frac{{kS\left( {{t_t} - {t_p}} \right)}}{d} \cdot d\tau \\ \Rightarrow - \frac{1}{{{t_t} - {t_p}}} \cdot d{t_t} = \frac{{kS}}{{mcd}} \cdot d\tau \\ \Rightarrow - \int_{100}^t {\frac{1}{{{t_t} - 25}}} \cdot d{t_t} = \int_0^{30} {\frac{{96\pi \cdot {{10}^{ - 4}}}}{{0,16\pi \cdot 4180 \cdot 5 \cdot {{10}^{ - 3}}}}} \cdot d\tau \end{array}$
Casio shift solve
$\begin{array}{l} \Rightarrow {t_t} \approx {93,8^0}\\ \Rightarrow \Delta {t_t} = 100 - 93,8 = {6,2^0}C \end{array}$
Trả lời ngắn: 6,2
Casio shift solve
$\begin{array}{l} \Rightarrow {t_t} \approx {93,8^0}\\ \Rightarrow \Delta {t_t} = 100 - 93,8 = {6,2^0}C \end{array}$
Trả lời ngắn: 6,2
Câu 5 Số hạt nucleon của 1 hạt nhân Po là bao nhiêu?
$A=210$
Trả lời ngắn: 210
Trả lời ngắn: 210
${{n}_{0}}=\frac{{{m}_{0}}}{M}=\frac{100}{210}=\frac{10}{21}mol$
${{N}_{0}}={{n}_{0}}{{N}_{A}}=\frac{10}{21}\cdot 6,02\cdot {{10}^{23}}\approx 2,87\cdot {{10}^{23}}$
$N={{N}_{0}}\cdot {{2}^{\frac{-t}{T}}}=2,87\cdot {{10}^{23}}\cdot {{2}^{\frac{-69}{138}}}\approx 20\cdot {{10}^{22}}$
Trả lời ngắn: 20
${{N}_{0}}={{n}_{0}}{{N}_{A}}=\frac{10}{21}\cdot 6,02\cdot {{10}^{23}}\approx 2,87\cdot {{10}^{23}}$
$N={{N}_{0}}\cdot {{2}^{\frac{-t}{T}}}=2,87\cdot {{10}^{23}}\cdot {{2}^{\frac{-69}{138}}}\approx 20\cdot {{10}^{22}}$
Trả lời ngắn: 20
