Tải ngay đề khảo sát môn Toán 2025 của Sở GD&ĐT Hải Phòng. Tài liệu luyện thi THPT Quốc gia chính xác, bám sát cấu trúc đề thi minh họa mới nhất.
Câu 1. Cho hàm số \( y = f(x) \) là hàm đa thức có đạo hàm \( f'(x) = x^2(x^2 - 1)(x - 2)^2 \). Số điểm cực trị của đồ thị hàm số là:
A. 1.
B. 4.
C. 3.
D. 2.
Câu 2. Với \( a, b \) là các số thực dương tùy ý, gọi \( x = \log_2 a, y = \log_2 b, P = \log_2 (a^2 b^3) \). Khẳng định nào sau đây là đúng?
A. \( P = x^2 y^3 \).
B. \( P = x^2 + y^3 \).
C. \( P = 2x + 3y \).
D. \( P = 6xy \).
Câu 3. Cho cấp số cộng \( (u_n) \) có \( u_1 = 3, u_6 = 27 \). Công sai d của cấp số cộng đã cho là:
A. d = 8.
B. d = 5.
C. d = 7.
D. d = 6.
Câu 4. Trong không gian \( Oxyz \), cho đường thẳng \( d: \dfrac{x - 3}{2} = \dfrac{y - 4}{-5} = \dfrac{z + 5}{3} \). Điểm nào sau đây thuộc đường thẳng \( d \)?
A. \( M(3; 4; -5) \)
B. \( N(2; -5; 3) \)
C. \( P(-3; -4; 5) \)
D. \( Q(2; 5; -3) \)
Câu 5. Tập nghiệm của bất phương trình: $ \left( \dfrac{3}{4} \right)^{2x - 1} \leq \left( \dfrac{4}{3} \right)^{x + 2} $ là:
A. \( S = (-\infty; 1] \)
B. \( S = (1; +\infty) \)
C. \( S = [1; +\infty) \)
D. \( S = (-\infty; 1) \)
Câu 6. Bảng sau đây biểu diễn mẫu số liệu ghép nhóm thống kê về nhu cầu mức giá mua nhà (đơn vị triệu đồng/m²) của khách hàng tại một công ty xây dựng:
Khoảng biến thiên \( R \) của mẫu số liệu ghép nhóm trên là:
A. \( R = 9 \)
B. \( R = 4 \)
C. \( R = 20 \)
D. \( R = 108 \)
Câu 7. Công thức tính thể tích \( V \) của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số \( y = f(x) \), trục \( Ox \) và hai đường thẳng \( x = a, x = b \) (\( a < b \)), xung quanh trục \( Ox \) là:
A. \( V = \int_a^b f^2(x)\,dx \)
B. \( V = \pi \int_a^b f(x)\,dx \)
C. \( V = \int_a^b |f(x)|\,dx \)
D. \( V = \pi \int_a^b f^2(x)\,dx \)
Câu 8. Hàm số \( y = f(x) \) có đồ thị như hình vẽ.
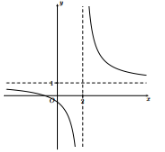
Đồ thị hàm số đã cho có tiệm cận ngang là:A. \( y = 1 \)
B. \( y = 2 \)
C. \( x = 1 \)
D. \( x = 2 \)
Câu 9. Cho hình chóp \( S.ABCD \) có đáy \( ABCD \) là hình bình hành, \( SA \) vuông góc với mặt phẳng \( (ABCD) \). Góc giữa hai đường thẳng nào sau đây bằng \( 90^\circ \)?
A. \( SA, SB \)
B. \( SB, AD \)
C. \( SA, BD \)
D. \( SA, SC \)
Câu 10. Trong không gian \( Oxyz \), mặt phẳng nào dưới đây nhận \( \vec{n} = (3;1;-7) \) là một vectơ pháp tuyến?
A. \( 3x - y - 7z + 1 = 0 \)
B. \( 3x + z + 7 = 0 \)
C. \( 3x + y - 7z - 3 = 0 \)
D. \( 3x + y - 7 = 0 \)
Câu 11. Cho hình hộp \( ABCD \cdot A_1B_1C_1D_1 \). Mệnh đề nào sau đây đúng?
A. \( |\vec{BA} + \vec{BB}_1 + \vec{BC}| = |\vec{BD}_1| \)
B. \( |\vec{AA}_1 + \vec{C}D + \vec{C}_1D_1| = 0 \)
C. \( |\vec{AB} - \vec{AD}_1| = |\vec{BD}_1| \)
D. \( |\vec{AB} + \vec{AD}_1| = |\vec{AC}_1| \)
Câu 12. Họ nguyên hàm của hàm số \( f(x) = x^{2024} \) là:
A. \( \int f(x)\,dx = x^{2025} + C \)
B. \( \int f(x)\,dx = \dfrac{1}{2023} \cdot x^{2023} + C \)
C. \( \int f(x)\,dx = 2024 \cdot x^{2024} + C \)
D. \( \int f(x)\,dx = \dfrac{1}{2025} \cdot x^{2025} + C \)
Câu 1. Cho hàm số \( f(x) = 2x^2 - 3 \) và \( F(x) \) là một nguyên hàm của hàm số \( f(x) \).
a) Cho \( g(x) = (ax^2 + bx + c) \cdot e^{3x} \) là một nguyên hàm của hàm số \( e^{3x} \cdot f(x) \), nếu $ \int_0^2 e^{3x} f(x)\, dx = m + \dfrac{n \cdot e^6}{27} $ Khi đó: \( 27m - n = -2 \).
b) Nếu \( F(0) = 1 \) thì \( F(2) = \dfrac{1}{3} \).
c) Ta có $ \int_0^2 f(x)\, dx = F(2) - F(0). $
d) Nếu $ \int_0^2 af(x)\, dx = 32 \text{ thì } a = -48. $
Câu 2. Cho hàm số \( y = \dfrac{x^2 + 3x + 3}{x + 2} \) có đồ thị \( (C) \) và 2 điểm \( A, B \) là hai điểm cực trị của \( (C) \).
a) Đường thẳng \( AB \) có phương trình là \( y = 2x + 1 \).
b) Đạo hàm của hàm số \( y' = \dfrac{x^2 + 4x + 3}{(x + 2)^2} \).
c) Hai điểm \( A \) và \( B \) đối xứng nhau qua đường thẳng \( \Delta \) có phương trình là \( x + 2y + 4 = 0 \).
d) Hai điểm \( A \) và \( B \) nằm ở hai phía của trục tung.
Câu 3. Trong không gian \( Oxyz \), cho mặt cầu \( (S) \) có phương trình $ (x + 1)^2 + (y + 2)^2 + (z + 3)^2 = 14 $ và điểm \( M(-1; -3; -2) \). Gọi \( I \) là tâm của mặt cầu \( (S) \).
a) Gọi \( (P) \) là mặt phẳng đi qua \( M \) và cắt mặt cầu \( (S) \) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Khi đó phương trình mặt phẳng \( (P) \) là \( y - z + 1 = 0 \).
b) Tọa độ tâm của mặt cầu \( (S) \) là \( I(-1; -2; -3) \).
c) Khoảng cách từ tâm \( I \) đến điểm \( M \) là \( IM = 2 \).
d) Điểm \( M \) nằm trong mặt cầu \( (S) \).
Câu 4. Một cửa hàng bán hai loại bóng đèn, trong đó có 65% bóng đèn màu trắng và 35% bóng đèn màu đỏ, các bóng đèn có kích thước như nhau. Các bóng đèn màu trắng có tỷ lệ hỏng là 2% và các bóng đèn màu đỏ có tỷ lệ hỏng là 3%. Một khách hàng chọn mua ngẫu nhiên 1 bóng đèn từ cửa hàng đó. Xét các biến cố: \( A \): “Khách hàng chọn được bóng màu trắng”; \( B \): “Khách hàng chọn được bóng không hỏng”. Khi đó:
a) \( P(B \mid A) = 0{,}98 \)
b) \( P(B) = 0{,}9765 \)
c) \( P(A) = 0{,}65 \)
d) \( P(B \mid \overline{A}) = 0{,}97 \)
Câu 2. Cho hình chóp \( S.ABC \) có đáy \( ABC \) là tam giác đều cạnh \( a \), cạnh bên \( SA \) vuông góc với mặt đáy, \( SA = \frac{a\sqrt{6}}{2} \). Biết khoảng cách từ điểm \( A \) đến mặt phẳng \( (SBC) \) là \( ma \) (với \( m \) là số thực dương). Khi đó giá trị của \( m \) bằng bao nhiêu (làm tròn kết quả đến hàng phần trăm)?
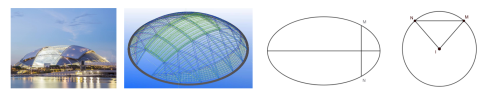
Câu 3. Sân vận động Sport Hub (Singapore) là sân có mái vòm kỳ vĩ nhất thế giới. Đây là nơi diễn ra lễ khai mạc Đại hội thể thao Đông Nam Á được tổ chức tại Singapore năm 2015. Nền sân là một elip \( (E) \) có trục lớn dài 150 m, trục bé dài 90 m. Nếu cắt sân vận động theo một mặt phẳng vuông góc với trục lớn của \( (E) \) và cắt elip ở \( M, N \) thì ta được thiết diện lớn là một phần của hình tròn có tâm \( I \) (phần tô đậm) với \( MN \) là một dây cung và góc \( MIN = 90^\circ \). Để lắp máy điều hòa không khí thì các kỹ sư cần tính thể tích phần không gian bên dưới mái che và bên trên mặt sân, coi như mặt sân là một mặt phẳng và thể tích vát lệch là mái không đáng kể. Biết rằng cách tính công suất cần đủ là 200 BTU/m³. Hỏi cần ít nhất bao nhiêu chiếc điều hòa công suất 50000 BTU?
Câu 4. Một căn bệnh có 1% dân số mắc phải. Một phương pháp chẩn đoán căn bệnh nói trên có tỷ lệ chính xác là 98% (với cả người bị bệnh và người không bị bệnh). Biết rằng nếu một người được sử dụng phương pháp trên để kiểm tra và cho kết quả dương tính (bị bệnh) thì xác suất người đó thực sự bị bệnh là \( \frac{9}{148} \) và là số tự nhiên. Hỏi y bằng bao nhiêu?
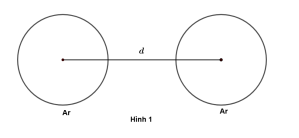
Câu 5. Xét hệ gồm hai nguyên tử khí Argon (Ar) ở trạng thái cơ bản, mỗi nguyên tử được coi là một khối cầu, khoảng cách d giữa hai nguyên tử bằng khoảng cách giữa tâm của hai khối cầu. Coi như khi không có tương tác bên ngoài nào tác động đến hệ, sự phụ thuộc của thế năng tương tác \( V(d) \) giữa hai nguyên tử khí vào khoảng cách d được xác định theo công thức $ V(d) = 4\varepsilon \left[\left(\frac{\sigma}{d}\right)^{12} - \left(\frac{\sigma}{d}\right)^6\right] $ với \( \varepsilon, \sigma \) là các hằng số đặc trưng cho từng khí hiếm. Đối với Ar, ta có \( \varepsilon = 0{,}930 \) và \( \sigma = 3{,}62 \). Biết rằng khi thế năng tương tác đạt nhỏ nhất thì hệ hai nguyên tử Ar là bền nhất, khoảng cách d mà hệ hai nguyên tử bền ổn nhất là bao nhiêu (làm tròn kết quả đến hàng phần trăm)? (Công thức \( V(d) \) có tên gọi là: Thế Lennard-Jones)
Câu 6. Trong không gian Oxyz, cho mặt cầu (S): $ x^2 + y^2 + z^2 - 4x + 2y - 2z - 3 = 0 $ và điểm \( A(5; 3; -2) \). Một đường thẳng \( d \) thay đổi luôn đi qua \( A \) và luôn cắt mặt cầu tại hai điểm phân biệt \( M, N \). Giá trị nhỏ nhất của biểu thức \( S = AM + 4AN \) là bao nhiêu (làm tròn kết quả đến hàng phần mười)?
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.Câu 1. Cho hàm số \( y = f(x) \) là hàm đa thức có đạo hàm \( f'(x) = x^2(x^2 - 1)(x - 2)^2 \). Số điểm cực trị của đồ thị hàm số là:
A. 1.
B. 4.
C. 3.
D. 2.
Câu 2. Với \( a, b \) là các số thực dương tùy ý, gọi \( x = \log_2 a, y = \log_2 b, P = \log_2 (a^2 b^3) \). Khẳng định nào sau đây là đúng?
A. \( P = x^2 y^3 \).
B. \( P = x^2 + y^3 \).
C. \( P = 2x + 3y \).
D. \( P = 6xy \).
Câu 3. Cho cấp số cộng \( (u_n) \) có \( u_1 = 3, u_6 = 27 \). Công sai d của cấp số cộng đã cho là:
A. d = 8.
B. d = 5.
C. d = 7.
D. d = 6.
Câu 4. Trong không gian \( Oxyz \), cho đường thẳng \( d: \dfrac{x - 3}{2} = \dfrac{y - 4}{-5} = \dfrac{z + 5}{3} \). Điểm nào sau đây thuộc đường thẳng \( d \)?
A. \( M(3; 4; -5) \)
B. \( N(2; -5; 3) \)
C. \( P(-3; -4; 5) \)
D. \( Q(2; 5; -3) \)
Câu 5. Tập nghiệm của bất phương trình: $ \left( \dfrac{3}{4} \right)^{2x - 1} \leq \left( \dfrac{4}{3} \right)^{x + 2} $ là:
A. \( S = (-\infty; 1] \)
B. \( S = (1; +\infty) \)
C. \( S = [1; +\infty) \)
D. \( S = (-\infty; 1) \)
Câu 6. Bảng sau đây biểu diễn mẫu số liệu ghép nhóm thống kê về nhu cầu mức giá mua nhà (đơn vị triệu đồng/m²) của khách hàng tại một công ty xây dựng:
| Nhóm | [10;14) | [14;18) | [18;22) | [22;26) | [26;30) |
|---|---|---|---|---|---|
| Tần số | 54 | 78 | 120 | 45 | 12 |
A. \( R = 9 \)
B. \( R = 4 \)
C. \( R = 20 \)
D. \( R = 108 \)
Câu 7. Công thức tính thể tích \( V \) của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số \( y = f(x) \), trục \( Ox \) và hai đường thẳng \( x = a, x = b \) (\( a < b \)), xung quanh trục \( Ox \) là:
A. \( V = \int_a^b f^2(x)\,dx \)
B. \( V = \pi \int_a^b f(x)\,dx \)
C. \( V = \int_a^b |f(x)|\,dx \)
D. \( V = \pi \int_a^b f^2(x)\,dx \)
Câu 8. Hàm số \( y = f(x) \) có đồ thị như hình vẽ.

Đồ thị hàm số đã cho có tiệm cận ngang là:A. \( y = 1 \)
B. \( y = 2 \)
C. \( x = 1 \)
D. \( x = 2 \)
Câu 9. Cho hình chóp \( S.ABCD \) có đáy \( ABCD \) là hình bình hành, \( SA \) vuông góc với mặt phẳng \( (ABCD) \). Góc giữa hai đường thẳng nào sau đây bằng \( 90^\circ \)?
A. \( SA, SB \)
B. \( SB, AD \)
C. \( SA, BD \)
D. \( SA, SC \)
Câu 10. Trong không gian \( Oxyz \), mặt phẳng nào dưới đây nhận \( \vec{n} = (3;1;-7) \) là một vectơ pháp tuyến?
A. \( 3x - y - 7z + 1 = 0 \)
B. \( 3x + z + 7 = 0 \)
C. \( 3x + y - 7z - 3 = 0 \)
D. \( 3x + y - 7 = 0 \)
Câu 11. Cho hình hộp \( ABCD \cdot A_1B_1C_1D_1 \). Mệnh đề nào sau đây đúng?
A. \( |\vec{BA} + \vec{BB}_1 + \vec{BC}| = |\vec{BD}_1| \)
B. \( |\vec{AA}_1 + \vec{C}D + \vec{C}_1D_1| = 0 \)
C. \( |\vec{AB} - \vec{AD}_1| = |\vec{BD}_1| \)
D. \( |\vec{AB} + \vec{AD}_1| = |\vec{AC}_1| \)
Câu 12. Họ nguyên hàm của hàm số \( f(x) = x^{2024} \) là:
A. \( \int f(x)\,dx = x^{2025} + C \)
B. \( \int f(x)\,dx = \dfrac{1}{2023} \cdot x^{2023} + C \)
C. \( \int f(x)\,dx = 2024 \cdot x^{2024} + C \)
D. \( \int f(x)\,dx = \dfrac{1}{2025} \cdot x^{2025} + C \)
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4.
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.Câu 1. Cho hàm số \( f(x) = 2x^2 - 3 \) và \( F(x) \) là một nguyên hàm của hàm số \( f(x) \).
a) Cho \( g(x) = (ax^2 + bx + c) \cdot e^{3x} \) là một nguyên hàm của hàm số \( e^{3x} \cdot f(x) \), nếu $ \int_0^2 e^{3x} f(x)\, dx = m + \dfrac{n \cdot e^6}{27} $ Khi đó: \( 27m - n = -2 \).
b) Nếu \( F(0) = 1 \) thì \( F(2) = \dfrac{1}{3} \).
c) Ta có $ \int_0^2 f(x)\, dx = F(2) - F(0). $
d) Nếu $ \int_0^2 af(x)\, dx = 32 \text{ thì } a = -48. $
Câu 2. Cho hàm số \( y = \dfrac{x^2 + 3x + 3}{x + 2} \) có đồ thị \( (C) \) và 2 điểm \( A, B \) là hai điểm cực trị của \( (C) \).
a) Đường thẳng \( AB \) có phương trình là \( y = 2x + 1 \).
b) Đạo hàm của hàm số \( y' = \dfrac{x^2 + 4x + 3}{(x + 2)^2} \).
c) Hai điểm \( A \) và \( B \) đối xứng nhau qua đường thẳng \( \Delta \) có phương trình là \( x + 2y + 4 = 0 \).
d) Hai điểm \( A \) và \( B \) nằm ở hai phía của trục tung.
Câu 3. Trong không gian \( Oxyz \), cho mặt cầu \( (S) \) có phương trình $ (x + 1)^2 + (y + 2)^2 + (z + 3)^2 = 14 $ và điểm \( M(-1; -3; -2) \). Gọi \( I \) là tâm của mặt cầu \( (S) \).
a) Gọi \( (P) \) là mặt phẳng đi qua \( M \) và cắt mặt cầu \( (S) \) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Khi đó phương trình mặt phẳng \( (P) \) là \( y - z + 1 = 0 \).
b) Tọa độ tâm của mặt cầu \( (S) \) là \( I(-1; -2; -3) \).
c) Khoảng cách từ tâm \( I \) đến điểm \( M \) là \( IM = 2 \).
d) Điểm \( M \) nằm trong mặt cầu \( (S) \).
Câu 4. Một cửa hàng bán hai loại bóng đèn, trong đó có 65% bóng đèn màu trắng và 35% bóng đèn màu đỏ, các bóng đèn có kích thước như nhau. Các bóng đèn màu trắng có tỷ lệ hỏng là 2% và các bóng đèn màu đỏ có tỷ lệ hỏng là 3%. Một khách hàng chọn mua ngẫu nhiên 1 bóng đèn từ cửa hàng đó. Xét các biến cố: \( A \): “Khách hàng chọn được bóng màu trắng”; \( B \): “Khách hàng chọn được bóng không hỏng”. Khi đó:
a) \( P(B \mid A) = 0{,}98 \)
b) \( P(B) = 0{,}9765 \)
c) \( P(A) = 0{,}65 \)
d) \( P(B \mid \overline{A}) = 0{,}97 \)
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Trong vật lý, một dao động điều hòa là dao động có phương trình chuyển động \( x(t) = A\cos(\omega t + \varphi) \), trong đó \( A \) là biên độ của dao động, \( \omega \) (rad/s) là tần số góc, \( \varphi \) (rad) là pha ban đầu. Động năng (Tiếng Anh: Kinetic energy) của một vật là năng lượng nó có được từ chuyển động của nó, được xác định bởi công thức $ W = \frac{1}{2}m \cdot v^2(t) $ (đơn vị J). Trong đó \( m \) (kg) là khối lượng của vật, \( v(t) \) (m/s) là vận tốc của vật tại thời điểm \( t \) (s). Giả sử một vật có khối lượng \( m = 100 \) (g) dao động điều hòa với phương trình chuyển động \( x(t) = 40\cos\left(200\pi t - \frac{\pi}{3}\right) \) (cm). Khi đó, động năng mà vật đó đạt giá trị lớn nhất bằng bao nhiêu (J) (làm tròn kết quả đến hàng đơn vị)?Câu 2. Cho hình chóp \( S.ABC \) có đáy \( ABC \) là tam giác đều cạnh \( a \), cạnh bên \( SA \) vuông góc với mặt đáy, \( SA = \frac{a\sqrt{6}}{2} \). Biết khoảng cách từ điểm \( A \) đến mặt phẳng \( (SBC) \) là \( ma \) (với \( m \) là số thực dương). Khi đó giá trị của \( m \) bằng bao nhiêu (làm tròn kết quả đến hàng phần trăm)?
Câu 3. Sân vận động Sport Hub (Singapore) là sân có mái vòm kỳ vĩ nhất thế giới. Đây là nơi diễn ra lễ khai mạc Đại hội thể thao Đông Nam Á được tổ chức tại Singapore năm 2015. Nền sân là một elip \( (E) \) có trục lớn dài 150 m, trục bé dài 90 m. Nếu cắt sân vận động theo một mặt phẳng vuông góc với trục lớn của \( (E) \) và cắt elip ở \( M, N \) thì ta được thiết diện lớn là một phần của hình tròn có tâm \( I \) (phần tô đậm) với \( MN \) là một dây cung và góc \( MIN = 90^\circ \). Để lắp máy điều hòa không khí thì các kỹ sư cần tính thể tích phần không gian bên dưới mái che và bên trên mặt sân, coi như mặt sân là một mặt phẳng và thể tích vát lệch là mái không đáng kể. Biết rằng cách tính công suất cần đủ là 200 BTU/m³. Hỏi cần ít nhất bao nhiêu chiếc điều hòa công suất 50000 BTU?

Câu 4. Một căn bệnh có 1% dân số mắc phải. Một phương pháp chẩn đoán căn bệnh nói trên có tỷ lệ chính xác là 98% (với cả người bị bệnh và người không bị bệnh). Biết rằng nếu một người được sử dụng phương pháp trên để kiểm tra và cho kết quả dương tính (bị bệnh) thì xác suất người đó thực sự bị bệnh là \( \frac{9}{148} \) và là số tự nhiên. Hỏi y bằng bao nhiêu?
Câu 5. Xét hệ gồm hai nguyên tử khí Argon (Ar) ở trạng thái cơ bản, mỗi nguyên tử được coi là một khối cầu, khoảng cách d giữa hai nguyên tử bằng khoảng cách giữa tâm của hai khối cầu. Coi như khi không có tương tác bên ngoài nào tác động đến hệ, sự phụ thuộc của thế năng tương tác \( V(d) \) giữa hai nguyên tử khí vào khoảng cách d được xác định theo công thức $ V(d) = 4\varepsilon \left[\left(\frac{\sigma}{d}\right)^{12} - \left(\frac{\sigma}{d}\right)^6\right] $ với \( \varepsilon, \sigma \) là các hằng số đặc trưng cho từng khí hiếm. Đối với Ar, ta có \( \varepsilon = 0{,}930 \) và \( \sigma = 3{,}62 \). Biết rằng khi thế năng tương tác đạt nhỏ nhất thì hệ hai nguyên tử Ar là bền nhất, khoảng cách d mà hệ hai nguyên tử bền ổn nhất là bao nhiêu (làm tròn kết quả đến hàng phần trăm)? (Công thức \( V(d) \) có tên gọi là: Thế Lennard-Jones)

Câu 6. Trong không gian Oxyz, cho mặt cầu (S): $ x^2 + y^2 + z^2 - 4x + 2y - 2z - 3 = 0 $ và điểm \( A(5; 3; -2) \). Một đường thẳng \( d \) thay đổi luôn đi qua \( A \) và luôn cắt mặt cầu tại hai điểm phân biệt \( M, N \). Giá trị nhỏ nhất của biểu thức \( S = AM + 4AN \) là bao nhiêu (làm tròn kết quả đến hàng phần mười)?
