Đề thi thử môn Toán 2025 lần 1 của Sở GD&ĐT Lai Châu – Tài liệu ôn luyện sát đề minh họa, có đáp án chi tiết giúp học sinh tự đánh giá năng lực hiệu quả.
Câu 1. Trọng lượng của 20 củ sâm trong một lô củ sâm được thu hoạch sau sáu năm trồng tại một cơ sở trồng sâm Lai Châu có bảng tần số ghép nhóm sau (đơn vị: gam):
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần mười) là:
A. 3,3.
B. 9,5.
C. 6,7.
D. 8,6.
Câu 2. Tập nghiệm của bất phương trình \( 3^{2x} > 9 \) là:
A. \( (-\infty; 2) \)
B. \( (2; +\infty) \)
C. \( (2; +\infty) \)
D. \( (5; +\infty) \)
Câu 3. Trong không gian \( Oxyz \), cho đường thẳng \( d: \) $ \begin{cases} x = 1 - 2t \\ y = 3 + 2t \\ z = -1 + 4t \end{cases} $
Điểm nào dưới đây thuộc đường thẳng \( d \)?
A. \( P(-1; -3; 1) \)
B. \( N(-2; 2; 4) \)
C. \( M(1; 3; -1) \)
D. \( Q(-1; 1; 2) \)
Câu 4. Cho hàm số \( f(x) \) liên tục trên \( \mathbb{R} \). Biết hàm số \( F(x) \) là một nguyên hàm của \( f(x) \) trên \( \mathbb{R} \) và \( F(3) = 5 \), \( F(1) = 1 \). Tích phân \( \int_{1}^{3} f(x) \, dx \) bằng:
A. \(-4\)
B. \(5\)
C. \(6\)
D. \(4\)
Câu 5. Cho hàm số \( y = f(x) \) xác định trên \( \mathbb{R} \) và có bảng biến thiên như sau.
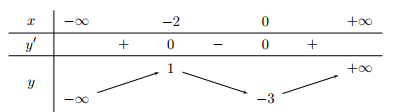
Hàm số \( y = f(x) \) nghịch biến trên khoảng nào dưới đây?
A. \( (2; 0) \)
B. \( (-3; +\infty) \)
C. \( (-\infty; -2) \)
D. \( (-3; 1) \)
Câu 6. Nghiệm của phương trình \( \log_2 x = 3 \) là:
A. \( x = \frac{3}{2} \)
B. \( x = 8 \)
C. \( x = 6 \)
D. \( x = 5 \)
Câu 7. Cấp số nhân \( (u_n) \) có \( u_1 = 2 \) và \( u_2 = -8 \). Công bội \( q \) của cấp số nhân là:
A. \( q = 10 \)
B. \( q = -\frac{1}{4} \)
C. \( q = -4 \)
D. \( q = -10 \)
Câu 8. Cho hình lập phương \( ABCD \cdot A'B'C'D' \).
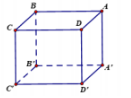
Góc giữa hai vectơ \( \overrightarrow{AB} \) và \( \overrightarrow{DC} \) là:
A. \( 60^\circ \)
B. \( 90^\circ \)
C. \( 45^\circ \)
D. \( 120^\circ \)
Câu 9. Đường cong là đồ thị của một trong bốn hàm số dưới đây.
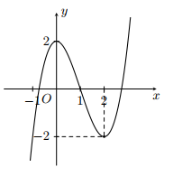
Hàm số đó là hàm số nào?
A. \( y = \frac{x + 1}{x + 2} \)
B. \( y = -x^2 - 6x + 2 \)
C. \( y = -x^2 + 3x^2 + 2 \)
D. \( y = x^3 - 3x^2 + 2 \)
Câu 10. Trong không gian với hệ trục tọa độ \( Oxyz \), mặt cầu (S) có phương trình $ (x - 5)^2 + (y + 2)^2 + (z - 3)^2 = 4 $ có bán kính bằng:
A. 16
B. 8
C. 2
D. 4
Câu 11. Khẳng định nào dưới đây đúng?
A. \( \int 2025^x \, dx = \frac{2025^{x+1}}{x+1} + C \)
B. \( \int 2025^x \, dx = \frac{2025^{x+1}}{\ln 2025} + C \)
C. \( \int 2025^x \, dx = 2025^x \cdot \ln 2025 + C \)
D. \( \int 2025^x \, dx = \frac{2025^x}{\ln 2025} + C \)
Câu 12. Cho hình chóp có diện tích mặt đáy là \( 3a^2 \) và chiều cao bằng \( 6a \). Thể tích của khối chóp bằng:
A. \( 18a^3 \)
B. \( 6a^3 \)
C. \( 9a^3 \)
D. \( 3a^3 \)
Câu 1. Khi gắn hệ tọa độ \( Oxyz \) (đơn vị trên mỗi trục tính theo kilômét) vào một sân bay, mặt phẳng \( (Oxy) \) trùng với mặt sân bay, một máy bay đang ở vị trí \( A(4; -5; 1) \) sẽ hạ cánh khẩn cấp ở vị trí \( B(1; 2; 0) \) trên đường băng \( EG \).
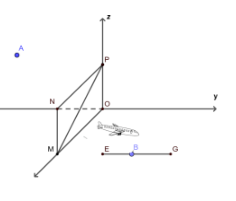
a) Phương trình đường thẳng \( AB \) là $ \begin{cases} x = 4 - 3t \\ y = -5 + 7t \\ z = 1 - t \end{cases} \quad (t\ \text{phút}). $
b) Góc trượt (góc giữa đường bay \( AB \) và mặt đất là mặt phẳng nằm ngang \( (Oxy) \)) không nằm trong phạm vi cho phép từ \( 2,5^\circ \) đến \( 9^\circ \).
c) Có một lớp mây mô phỏng bởi mặt phẳng \( (P) \) đi qua ba điểm \( M(5; 0; 0) \), \( N(0; -1; 0) \), \( P(0; 0; 2) \). Máy bay xuyên qua đám mây tại điểm \( C \) có độ cao lớn hơn ước đoán (đơn vị là) 346 m.
d) Biết rằng tầm nhìn của người phi công sau khi rã khỏi đám mây là 800 m. Sau khi rã khỏi đám mây, người phi công đặt được quy định an toàn bay là người phi công phải nhìn thấy điểm đầu \( E(2; 0; 5.0) \) của đường băng ở độ cao tối thiểu 150 m.
Câu 2. Cho hàm số \( f(x) = x - \sin 2x \).
a) \( \int\limits_{-\frac{\pi}{2}}^{\frac{\pi}{2}} f(x)\, dx = -\frac{\pi}{2},\ f(\pi) = \pi. \)
b) \( f'(x) = 1 - \cos 2x. \)
c) Phương trình \( f'(x) = 0 \) trên đoạn \( \left[ -\frac{\pi}{2}; \pi \right] \) có tập nghiệm là
\( T = \left\{ -\frac{\pi}{2},\ \frac{\pi}{6},\ \frac{5\pi}{6} \right\} \)
d) Tổng giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn \( \left[ -\frac{\pi}{2}; \pi \right] \) bằng
\( \frac{3\pi}{2} + \frac{\sqrt{3}}{2} \)
Câu 3. Một chiếc hộp chứa 9 quả cầu gồm 4 quả màu xanh, 3 quả màu đỏ và 2 quả màu vàng. Lấy ngẫu nhiên 3 quả cầu từ hộp đó.
a) Số cách lấy ngẫu nhiên 3 quả cầu từ hộp đó là 84.
b) Số cách lấy được 3 quả cầu cùng có màu đỏ là 20.
c) Xác suất lấy được 3 quả cầu không có quả màu đỏ bằng \( \frac{1}{84} \)
d) Xác suất lấy được 3 quả cầu có ít nhất 1 quả màu đỏ bằng \( \frac{83}{84} \)
Câu 4. Tại một khu di tích vào ngày lễ hội hằng năm, tốc độ thay đổi lượng khách tham quan được biểu diễn bằng hàm số
\( Q'(t) = t^3 - 72t^2 + 288t \), trong đó \( t \) tính bằng giờ \( (0 \leq t \leq 13) \), \( Q'(t) \) tính bằng khách/giờ.
Tại thời điểm \( t = 2 \) giờ đã có 500 người có mặt.
a) Lượng khách tham quan được biểu diễn bởi hàm số
\( Q(t) = t^4 - 24t^3 + 144t^2 + C \)
b) Tại thời điểm \( t = 5 \) giờ, lượng khách tham quan là 1325 người.
c) Lượng khách tham quan lớn nhất là 1296 người.
d) Tại thời điểm \( t = 13 \) giờ, lượng khách tham quan là lớn nhất.
Hình chiếu vuông góc của \( S \) lên mặt phẳng đáy trùng với trung điểm \( H \) của \( AD \) và \( SH = \dfrac{\sqrt{6}}{2} \).
Tính khoảng cách từ \( B \) đến mặt phẳng \( (SCD) \) (làm tròn kết quả đến hàng phần trăm).
Câu 2. Nam và ba người bạn lên kế hoạch cho một chuyến đi phượt xuyên Việt, ghé thăm 4 thành phố: Hà Nội, Đà Nẵng, Thành phố Hồ Chí Minh (TP.HCM) và Cần Thơ. Họ xuất phát từ Hà Nội, đi qua tất cả các thành phố còn lại đúng một lần rồi quay về Hà Nội. Bảng chi phí nhiên liệu (tính bằng lít xăng) giữa các thành phố như sau:
Xe của nhóm hiện đã có sẵn 150 lít xăng. Để hoàn thành hành trình, họ cần đổ thêm ít nhất bao nhiêu lít xăng?
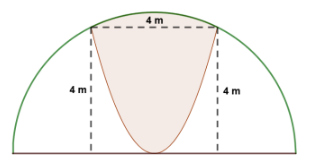
Câu 3. Khuôn viên nhà bạn Thùy Dương có dạng nửa hình tròn, trên đó người thiết kế phần để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm và có trục đối xứng vuông góc với đường kính của nửa hình tròn, hai đầu mút của cánh hoa nằm trên nửa đường tròn và cách nhau một khoảng bằng 4 m. Phần còn lại của khuôn viên dành để trồng cỏ Nhung Nhật. Biết các kích thước cho như hình vẽ, chi phí trồng hoa và cỏ Nhung Nhật tương ứng là 250.000 đồng/m² và 150.000 đồng/m². Hỏi chi phí để trồng hoa và trồng cỏ Nhung Nhật trong khuôn viên đó ít nhất bao nhiêu triệu đồng (làm tròn kết quả đến hàng phần chục)?
Câu 4. Khi gắn hệ tọa độ \( Oxyz \) (đơn vị trên mỗi trục tính theo kilômét) vào không gian, người ta thấy rằng một không gian phủ sóng điện thoại có dạng một hình cầu \( (S) \) (tập hợp những điểm nằm trên và nằm trong mặt cầu tương ứng). Biết mặt cầu có phương trình: $ x^2 + y^2 + z^2 - 4x - 6y - 2z + 5 = 0. $ Khoảng cách xa nhất giữa hai điểm thuộc vùng phủ sóng là bao nhiêu kilômét?
Câu 5. Một xưởng sản xuất cửa nhôm kính uốn vòm gồm phần dưới là hình chữ nhật có chiều rộng \( x \) (cm), chiều dài \( y \) (cm), phần vòm là hình bán nguyệt có bán kính \( \dfrac{x}{2} \) (cm). Biết chu vi của cửa không đổi là 8 m.
Biết đơn giá làm cửa tính theo m² là 1.600.000 đồng. Khi diện tích của cửa lớn nhất thì cửa trị giá bao nhiêu triệu đồng (làm tròn đến hàng phần mười)?

Câu 6. Gọi \( S \) là tập hợp các số tự nhiên gồm 6 chữ số đôi một khác nhau được lập từ tập \( A = \{0, 1, 2, 3, 4, 5, 6\} \). Lấy ngẫu nhiên một số từ \( S \). Tính xác suất sao cho lấy được số có dạng $\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}} $ thỏa mãn điều kiện \( a_1 + a_2 = a_3 + a_4 = a_5 + a_6 \) (kết quả để dưới dạng số thập phân và làm tròn đến hàng phần trăm).
PHẦN 1. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.Câu 1. Trọng lượng của 20 củ sâm trong một lô củ sâm được thu hoạch sau sáu năm trồng tại một cơ sở trồng sâm Lai Châu có bảng tần số ghép nhóm sau (đơn vị: gam):
| Nhóm | (40;45) | (45;50) | (50;55) | (55;60) |
|---|---|---|---|---|
| Tần số | 3 | 7 | 8 | 2 |
A. 3,3.
B. 9,5.
C. 6,7.
D. 8,6.
Câu 2. Tập nghiệm của bất phương trình \( 3^{2x} > 9 \) là:
A. \( (-\infty; 2) \)
B. \( (2; +\infty) \)
C. \( (2; +\infty) \)
D. \( (5; +\infty) \)
Câu 3. Trong không gian \( Oxyz \), cho đường thẳng \( d: \) $ \begin{cases} x = 1 - 2t \\ y = 3 + 2t \\ z = -1 + 4t \end{cases} $
Điểm nào dưới đây thuộc đường thẳng \( d \)?
A. \( P(-1; -3; 1) \)
B. \( N(-2; 2; 4) \)
C. \( M(1; 3; -1) \)
D. \( Q(-1; 1; 2) \)
Câu 4. Cho hàm số \( f(x) \) liên tục trên \( \mathbb{R} \). Biết hàm số \( F(x) \) là một nguyên hàm của \( f(x) \) trên \( \mathbb{R} \) và \( F(3) = 5 \), \( F(1) = 1 \). Tích phân \( \int_{1}^{3} f(x) \, dx \) bằng:
A. \(-4\)
B. \(5\)
C. \(6\)
D. \(4\)
Câu 5. Cho hàm số \( y = f(x) \) xác định trên \( \mathbb{R} \) và có bảng biến thiên như sau.

Hàm số \( y = f(x) \) nghịch biến trên khoảng nào dưới đây?
A. \( (2; 0) \)
B. \( (-3; +\infty) \)
C. \( (-\infty; -2) \)
D. \( (-3; 1) \)
Câu 6. Nghiệm của phương trình \( \log_2 x = 3 \) là:
A. \( x = \frac{3}{2} \)
B. \( x = 8 \)
C. \( x = 6 \)
D. \( x = 5 \)
Câu 7. Cấp số nhân \( (u_n) \) có \( u_1 = 2 \) và \( u_2 = -8 \). Công bội \( q \) của cấp số nhân là:
A. \( q = 10 \)
B. \( q = -\frac{1}{4} \)
C. \( q = -4 \)
D. \( q = -10 \)
Câu 8. Cho hình lập phương \( ABCD \cdot A'B'C'D' \).

Góc giữa hai vectơ \( \overrightarrow{AB} \) và \( \overrightarrow{DC} \) là:
A. \( 60^\circ \)
B. \( 90^\circ \)
C. \( 45^\circ \)
D. \( 120^\circ \)
Câu 9. Đường cong là đồ thị của một trong bốn hàm số dưới đây.

Hàm số đó là hàm số nào?
A. \( y = \frac{x + 1}{x + 2} \)
B. \( y = -x^2 - 6x + 2 \)
C. \( y = -x^2 + 3x^2 + 2 \)
D. \( y = x^3 - 3x^2 + 2 \)
Câu 10. Trong không gian với hệ trục tọa độ \( Oxyz \), mặt cầu (S) có phương trình $ (x - 5)^2 + (y + 2)^2 + (z - 3)^2 = 4 $ có bán kính bằng:
A. 16
B. 8
C. 2
D. 4
Câu 11. Khẳng định nào dưới đây đúng?
A. \( \int 2025^x \, dx = \frac{2025^{x+1}}{x+1} + C \)
B. \( \int 2025^x \, dx = \frac{2025^{x+1}}{\ln 2025} + C \)
C. \( \int 2025^x \, dx = 2025^x \cdot \ln 2025 + C \)
D. \( \int 2025^x \, dx = \frac{2025^x}{\ln 2025} + C \)
Câu 12. Cho hình chóp có diện tích mặt đáy là \( 3a^2 \) và chiều cao bằng \( 6a \). Thể tích của khối chóp bằng:
A. \( 18a^3 \)
B. \( 6a^3 \)
C. \( 9a^3 \)
D. \( 3a^3 \)
PHẦN 2. Thí sinh trả lời từ câu 1 đến câu 4.
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.Câu 1. Khi gắn hệ tọa độ \( Oxyz \) (đơn vị trên mỗi trục tính theo kilômét) vào một sân bay, mặt phẳng \( (Oxy) \) trùng với mặt sân bay, một máy bay đang ở vị trí \( A(4; -5; 1) \) sẽ hạ cánh khẩn cấp ở vị trí \( B(1; 2; 0) \) trên đường băng \( EG \).

a) Phương trình đường thẳng \( AB \) là $ \begin{cases} x = 4 - 3t \\ y = -5 + 7t \\ z = 1 - t \end{cases} \quad (t\ \text{phút}). $
b) Góc trượt (góc giữa đường bay \( AB \) và mặt đất là mặt phẳng nằm ngang \( (Oxy) \)) không nằm trong phạm vi cho phép từ \( 2,5^\circ \) đến \( 9^\circ \).
c) Có một lớp mây mô phỏng bởi mặt phẳng \( (P) \) đi qua ba điểm \( M(5; 0; 0) \), \( N(0; -1; 0) \), \( P(0; 0; 2) \). Máy bay xuyên qua đám mây tại điểm \( C \) có độ cao lớn hơn ước đoán (đơn vị là) 346 m.
d) Biết rằng tầm nhìn của người phi công sau khi rã khỏi đám mây là 800 m. Sau khi rã khỏi đám mây, người phi công đặt được quy định an toàn bay là người phi công phải nhìn thấy điểm đầu \( E(2; 0; 5.0) \) của đường băng ở độ cao tối thiểu 150 m.
Câu 2. Cho hàm số \( f(x) = x - \sin 2x \).
a) \( \int\limits_{-\frac{\pi}{2}}^{\frac{\pi}{2}} f(x)\, dx = -\frac{\pi}{2},\ f(\pi) = \pi. \)
b) \( f'(x) = 1 - \cos 2x. \)
c) Phương trình \( f'(x) = 0 \) trên đoạn \( \left[ -\frac{\pi}{2}; \pi \right] \) có tập nghiệm là
\( T = \left\{ -\frac{\pi}{2},\ \frac{\pi}{6},\ \frac{5\pi}{6} \right\} \)
d) Tổng giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn \( \left[ -\frac{\pi}{2}; \pi \right] \) bằng
\( \frac{3\pi}{2} + \frac{\sqrt{3}}{2} \)
Câu 3. Một chiếc hộp chứa 9 quả cầu gồm 4 quả màu xanh, 3 quả màu đỏ và 2 quả màu vàng. Lấy ngẫu nhiên 3 quả cầu từ hộp đó.

a) Số cách lấy ngẫu nhiên 3 quả cầu từ hộp đó là 84.
b) Số cách lấy được 3 quả cầu cùng có màu đỏ là 20.
c) Xác suất lấy được 3 quả cầu không có quả màu đỏ bằng \( \frac{1}{84} \)
d) Xác suất lấy được 3 quả cầu có ít nhất 1 quả màu đỏ bằng \( \frac{83}{84} \)
Câu 4. Tại một khu di tích vào ngày lễ hội hằng năm, tốc độ thay đổi lượng khách tham quan được biểu diễn bằng hàm số
\( Q'(t) = t^3 - 72t^2 + 288t \), trong đó \( t \) tính bằng giờ \( (0 \leq t \leq 13) \), \( Q'(t) \) tính bằng khách/giờ.
Tại thời điểm \( t = 2 \) giờ đã có 500 người có mặt.
a) Lượng khách tham quan được biểu diễn bởi hàm số
\( Q(t) = t^4 - 24t^3 + 144t^2 + C \)
b) Tại thời điểm \( t = 5 \) giờ, lượng khách tham quan là 1325 người.
c) Lượng khách tham quan lớn nhất là 1296 người.
d) Tại thời điểm \( t = 13 \) giờ, lượng khách tham quan là lớn nhất.
PHẦN 3. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Cho khối chóp \( S.ABCD \) có đáy \( ABCD \) là hình thang vuông tại \( A \) và \( B \), \( AB = BC = 1 \), \( AD = 2 \).Hình chiếu vuông góc của \( S \) lên mặt phẳng đáy trùng với trung điểm \( H \) của \( AD \) và \( SH = \dfrac{\sqrt{6}}{2} \).
Tính khoảng cách từ \( B \) đến mặt phẳng \( (SCD) \) (làm tròn kết quả đến hàng phần trăm).
Câu 2. Nam và ba người bạn lên kế hoạch cho một chuyến đi phượt xuyên Việt, ghé thăm 4 thành phố: Hà Nội, Đà Nẵng, Thành phố Hồ Chí Minh (TP.HCM) và Cần Thơ. Họ xuất phát từ Hà Nội, đi qua tất cả các thành phố còn lại đúng một lần rồi quay về Hà Nội. Bảng chi phí nhiên liệu (tính bằng lít xăng) giữa các thành phố như sau:
| Hà Nội | Đà Nẵng | TP.HCM | Cần Thơ | |
|---|---|---|---|---|
| Hà Nội | 0 | 40 | 90 | 110 |
| Đà Nẵng | 40 | 0 | 50 | 70 |
| TP.HCM | 90 | 50 | 0 | 30 |
| Cần Thơ | 110 | 70 | 30 | 0 |
Câu 3. Khuôn viên nhà bạn Thùy Dương có dạng nửa hình tròn, trên đó người thiết kế phần để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm và có trục đối xứng vuông góc với đường kính của nửa hình tròn, hai đầu mút của cánh hoa nằm trên nửa đường tròn và cách nhau một khoảng bằng 4 m. Phần còn lại của khuôn viên dành để trồng cỏ Nhung Nhật. Biết các kích thước cho như hình vẽ, chi phí trồng hoa và cỏ Nhung Nhật tương ứng là 250.000 đồng/m² và 150.000 đồng/m². Hỏi chi phí để trồng hoa và trồng cỏ Nhung Nhật trong khuôn viên đó ít nhất bao nhiêu triệu đồng (làm tròn kết quả đến hàng phần chục)?
Câu 4. Khi gắn hệ tọa độ \( Oxyz \) (đơn vị trên mỗi trục tính theo kilômét) vào không gian, người ta thấy rằng một không gian phủ sóng điện thoại có dạng một hình cầu \( (S) \) (tập hợp những điểm nằm trên và nằm trong mặt cầu tương ứng). Biết mặt cầu có phương trình: $ x^2 + y^2 + z^2 - 4x - 6y - 2z + 5 = 0. $ Khoảng cách xa nhất giữa hai điểm thuộc vùng phủ sóng là bao nhiêu kilômét?
Câu 5. Một xưởng sản xuất cửa nhôm kính uốn vòm gồm phần dưới là hình chữ nhật có chiều rộng \( x \) (cm), chiều dài \( y \) (cm), phần vòm là hình bán nguyệt có bán kính \( \dfrac{x}{2} \) (cm). Biết chu vi của cửa không đổi là 8 m.
Biết đơn giá làm cửa tính theo m² là 1.600.000 đồng. Khi diện tích của cửa lớn nhất thì cửa trị giá bao nhiêu triệu đồng (làm tròn đến hàng phần mười)?

Câu 6. Gọi \( S \) là tập hợp các số tự nhiên gồm 6 chữ số đôi một khác nhau được lập từ tập \( A = \{0, 1, 2, 3, 4, 5, 6\} \). Lấy ngẫu nhiên một số từ \( S \). Tính xác suất sao cho lấy được số có dạng $\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}} $ thỏa mãn điều kiện \( a_1 + a_2 = a_3 + a_4 = a_5 + a_6 \) (kết quả để dưới dạng số thập phân và làm tròn đến hàng phần trăm).
